Accelerating Queries with Group-By and Join By Groupjoin

梁辰

数据库内核开发

这篇paper介绍了HyPer中引入的groupjoin算子，针对 join + group by这种query，可以在某些前提条件下，在join的过程中同时完成grouping+agg的计算。

比如用hash table来实现hash join和group by，就可以避免再创建一个hash table，尤其当join的数据量很大，产生的group结果又较少时，可以很好的提升执行效率。

文中提出了2个等价的变换：

left outer join + group by => groupjoin
inner join + group by => groupjoin

这个变换的前提是存在某些Functional Dependency！

这种变换是一种特定情况下针对物理实现的优化，所以总是benificial的，不会带来负面效果。

基本术语

基本概念及标记

在之前涉及HyPer的文章中，已经介绍了F(e) 这个符号，表示e中引用的属性集合。

{ \cdot }s 表示set（无重复），{ \cdot }b表示bag（multiset，可重复）。

\Pi 表示投影， \Pi^{D} 表示去重投影。

\chi a:e2 (e1) 表示mapping操作，对于e1的每条Input tuple，计算e2这个表达式，结果保存在一个新的属性列a中。

对于 = 操作，如果null = null，结果是unknown，但在grouping的计算中,null = null是成立的，用在=上加(.)来表示。

A -> TID(e) 表示属性列集合A的元素，可以functional决定e的一行数据。

\bot_{A} 表示在属性列集合A上，均为NULL值。

聚集函数的特性

如果聚集函数可以分步骤完成（局部 -> 全局），称这种聚集函数是 decomposable 的：

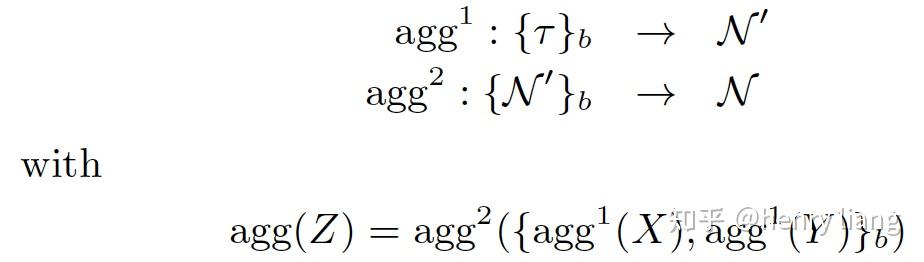
其中 Z = X \cup Y ，且X, Y无交集。这种属性可以保证聚集操作被拆分为任意粒度，各自独立做局部计算，然后再做全局汇总，仍可得到正确结果。

上图是SQL中最常见的decomposable聚集函数，其中 count^{NN} 是对non-null值的计数。

扩展这个概念来描述对多个属性列，各自独立的计算agg函数的aggregation vector:

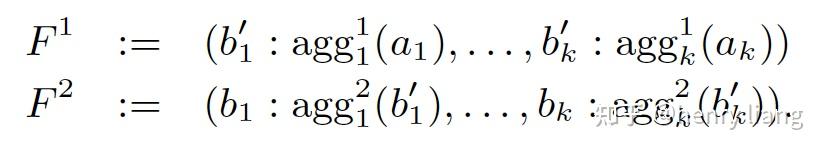
其中每个aggi表示第i个聚集函数，其局部的聚集结果是 b_{i}^{'} ，bi则是全局的聚集结果。

如果对于一个aggregation vector F以及对应的两个expression e1/e2。可以做如下拆分：

F = F1 \circ F2 且 F(F1) \cap A(e2) = \phi 且 F(F2) \cap A(e1) = \phi

即F1和F2各自表示一部分vector中的一部分聚集函数，且F1仅引入e2的列，F2仅引用e1的列，则称F是 splittable 的。

例如sum(a1 + a2) = sum(a1) + sum(a2)，这个sum聚集是可以针对不同属性列拆开计算的。

注意，decomposability 和 splittability 是可以做groupjoin的前提条件！

此外，一些聚集函数是对重复值不敏感的，比如min/max/aggr(distinct)，其他则是敏感的，比如普通的sum/count/avg。

Left Outer Join

这里对其描述进行了一个扩展，允许在join不上做填充时，对某些指定的列，填充某个default value，而不是NULL值：

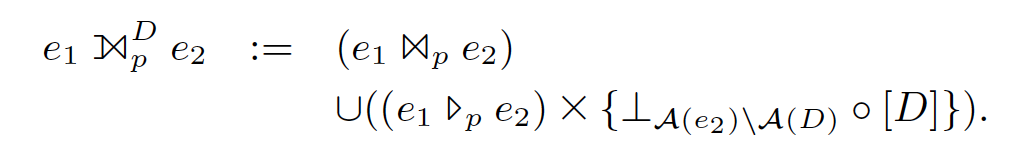
以上公式中，D = d1 : c1; ... dk : ck，表示在di这些列上，设置默认的填充值为ci。这对于后面groupjoin的等价转换时有意义。

Group By

这里只列出一个简单形式的标记方式，已经足够用来理解后续的内容：

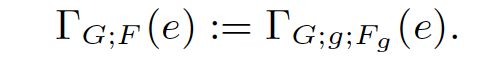
其中G是group by列集合，g是聚集结果向量，Fg是聚集函数vector。

GroupJoin

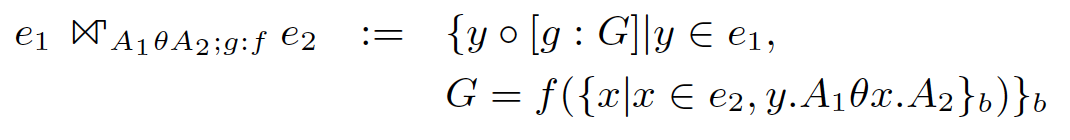
GroupJoin是一种物理上的优化实现，方式是：

两个表e1/e2执行join A_{1} \theta A_{2} ，对于外表e1的一行数据y，内表e2所有可以与其join上的行集合{x}，形成一个bag (multiset) ，对这个bag应用函数f后得到的一个标量结果并append到y后面，构成了新的属性列g。而这一组数据，就 完整的对应了实际的一个分组数据！ 这样当join结束时，所有分组的计算都完成了。

简略的记法是

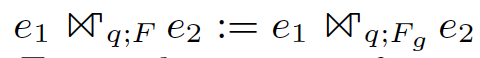
例如这样一个groupjoin:

select e1.a1, sum(e2.b2) as c2
from e1 join e2 on e1.a1 = e2.a2
group by e1.a1;

其执行过程如下

先在e1.a1列上，build hash table
聚集函数c2由于是sum，其值初始化为0
e2的每行数据t2进行probe，如果可以匹配a1 = a2，则更新t2中的属性列所对应的那个聚集函数，这里是sum(b2)，累计e2.b2到结果c2中。
probe完成，所有e1行的聚集函数已经计算完成，结果输出

注意groupJoin的一个特点是， 外表e1的输入是没有重复的 ，这样在groupjoin完成后生成的分组列+聚集函数才能没有重复，从而得到最终聚集结果。

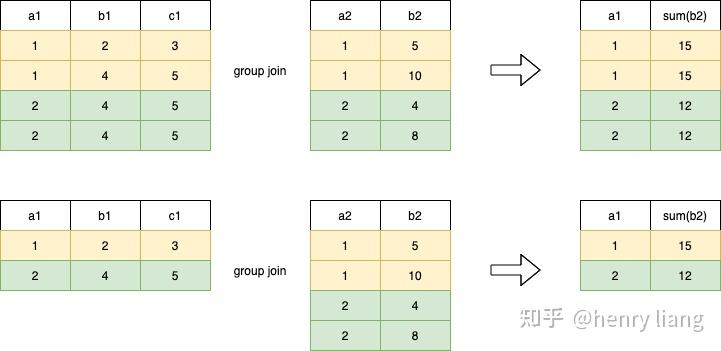
例如上图中，第一个groupjoin，由于左表有重复值，最终结果中也按照a1存在重复值，不是最终结果（如果要得到最终聚集结果，需要二次聚集）。而第二个groupjoin，左表没有重复值，因此可以得到正确结果。

等价形式

group的基本特性

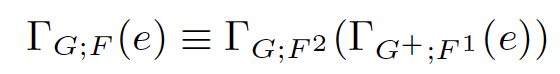
G是G+的子集，也就是先在一个更细粒度的分区(G+决定)，做局部聚集，再在更粗粒度的最终group列上，做全局聚集，和直接在粗粒度做全局聚集效果相同。

存在functional dependency时可以更进一步，如果 G -> G’ 这种FD成立，则如下等式成立：

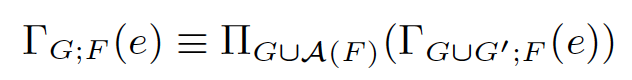
虽然G'中包含更多分组列，但由于FD的决定关系，这些列不会改变G所决定的分组情况，所以加不加这些冗余列，结果没有区别，这样就可以引导我们对Group列进行化简，去掉被决定的冗余列，使group列数量最小化提高计算效率。这和上一篇SCOPE优化器中提到的group列的reduction策略是一致的：

假设 H -> G，则多出来的冗余列记为 G\H。在聚集时，这些列的值会被H的值所唯一决定，所以每个分组只需要copy一下这些列的值就可以了。

如果每个group在join之后只有一行数据，即对于join的结果e， G -> TID(e)，则可以直接去掉group by + agg。

Groupjoin的基本特性

GroupJoin可以描述成等价的形式：

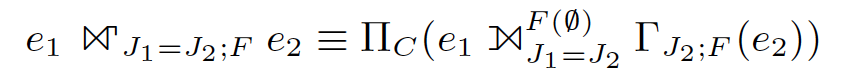
根据groupjoin的语义，e1的一行t1，对应的e2的所有join行t2集合，构成一个分组，如果聚集函数F只针对e2的列，则可以先对e2，针对J2做聚集，然后再和t1 join，结果是等价的。

这里有一个特例，就是count(*)的处理，当join不上时，e2这边是空bag，count(*) = 0，但实际中因为有t1这行，count(*)应该是1，这时可以使用前面提到的带有default value的left outer join，对count(*)的列设置default value为1，即可。

应用条件

left outer join + group by => groupjoin

有了以上的一系列等价变形后，paper给出可以将left outer join + group by转换为groupjoin的前提条件，先补充几个标记法：

对于分组列 G，其包含G1 + G2，分别属于e1,e2左右两个relation。

G_{i}^{+} = G_{i} \cup J_{i} ，也就是任一侧的分组列+join列

F(F) \subseteq A(e2). 即只针对e2表的列做聚集

满足以上4个条件，则可以应用groupjoin的执行方式。让我们逐条看下

condition 1意味着一个分组G只对应e1表的一行数据，不会有e1的两行数据属于同一个分组。这和前面讨论的，对e1的每一行，join的结果形成一个分组的结论一致。此外 G \rightarrow G_{2}^{+} 的意思是， G_{2}^{+} 相对于G来说并不是一个更细粒度的分组！如果是更细的分组，会导致G的一组数据，可能包含多个G2 + J2值对应的分组，因此一次join结果是不完全的。

condition 2意味着J2 -> G2，也就是J2的join值确定，e2表的group列值也就确定了，即具有相同join值的结果，也同时具有相同的G2值，如果这条不成立，则一次join的结果会属于不同的分组。

condition 3其实是可以放松的，列在这里个人理解是从实现简单的角度考虑。

condition 4要求聚集函数对于NULL值的处理与空集的处理一致，例如count(NULL) = count( \phi )。

Inner join + group => groupjoin

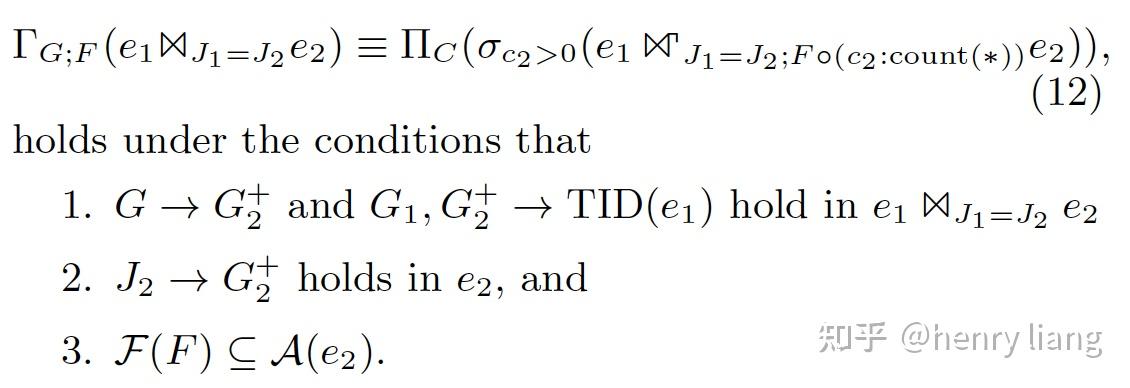
转换的前提条件基本和上节一致，只是增加了谓词c2 > 0，可以拒绝掉e2上填充的NULL值。

示例

以TPC-H(SF=1) Q13为例

select c_count, count(*) as custdist (select c_custkey, count(o_orderkey) as c_count from customer left outer join orders on c_custkey = o_custkey and o comment not like '%special%requests%'