介绍一些Scaling Laws

1、什么是scaling laws？

Scaling Laws简单介绍就是：随着模型大小、数据集大小和用于训练的计算浮点数的增加，模型的性能会提高。并且为了获得最佳性能，所有三个因素 必须同时放大 。当不受其他两个因素的制约时，模型性能与每个单独的因素都有 幂律关系 [1] 。

2、Scaling Laws重要吗？

由于当不受其他两个因素的制约时，模型性能与每个单独的因素都有 幂律关系 。因此，当这种幂率关系出现时，我们是可以提前对模型的性能进行预测的。比如GPT4的报告中[2]，明确指出：

The results on the 3rd easiest bucket are shown in Figure 2, showing that the resulting predictions were very accurate for this subset of HumanEval problems where we can accurately estimate log(pass_rate) for several smaller models.

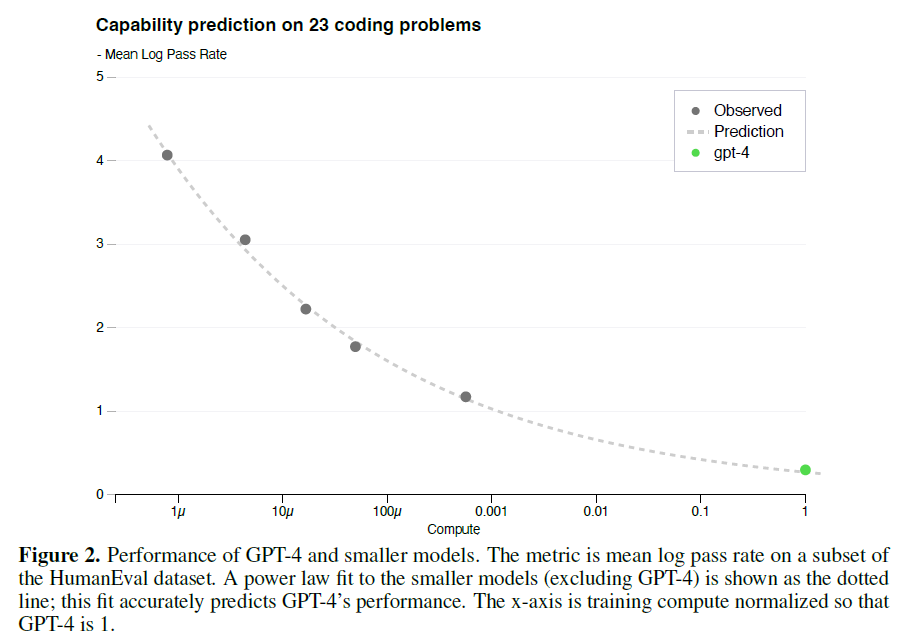
简单翻译一下就是，GPT4在这23个问题上的性能预测，可以通过比GPT4小1000倍的模型预测得来。也就是说GPT4还没开始训练，它在这23个问题上的性能就已经知道了。所以，可想而知，Scaling Laws对于大模型的训练而言 很重要 ！

3、如何验证自己的预训练模型是否满足Scaling Laws？

既然Scaling Laws这么重要，那么如何看自己的预训练模型是否满足Scaling Laws呢？换句说，如果我们准备开始预训练一个很大的模型，应该如何利用Scaling Laws呢？

这里，首先Google在PaLM2上做了尝试[3]，比较成功的让PaLM2满足Scaling Laws。那接下来就结合OpenAI和Google的工作详细说一下具体的做法。

3.1 确定模型结构以及参数

首先，需要确定我们要预训练的模型的结构，大部分都是类似GPT4的结构，以及我们期望的模型的参数有多大。这里有一个非常重要的估算，就是浮点运算量（FLOPs） C 、模型参数 N 以及训练的token数 D 之间存在关系： C\sim6ND 。（注意，这里的结果表明你的模型和GPT的模型是相似的）

具体的证明可以参考下图：

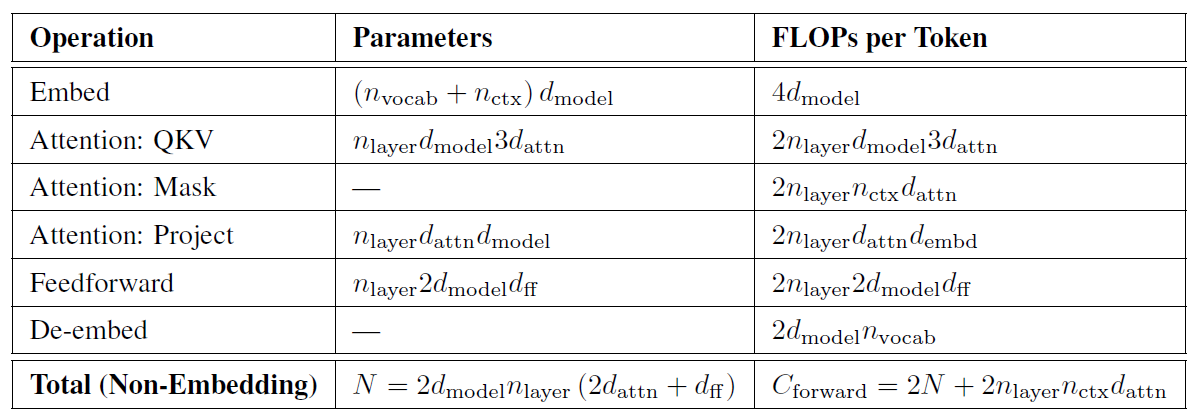
这里的模型参数 N 是不考虑Embed的，FLOPs也是不考虑Embed和De-embed。

3.2 训练多个不同参数的模型

确定了模型的框架以及期望训练的参数后，我们可以在多个比期望参数小的模型上做预训练，并且统计多个实验结果，如GPT3的图所示：随着训练的进行（计算量 C ），小的模型出现收敛，大的模型loss也迅速下降。拟合小模型每条曲线的下降趋势（可能需要多次拟合），可以得到损失值 L 与计算量 C 的关系（幂次关系）。

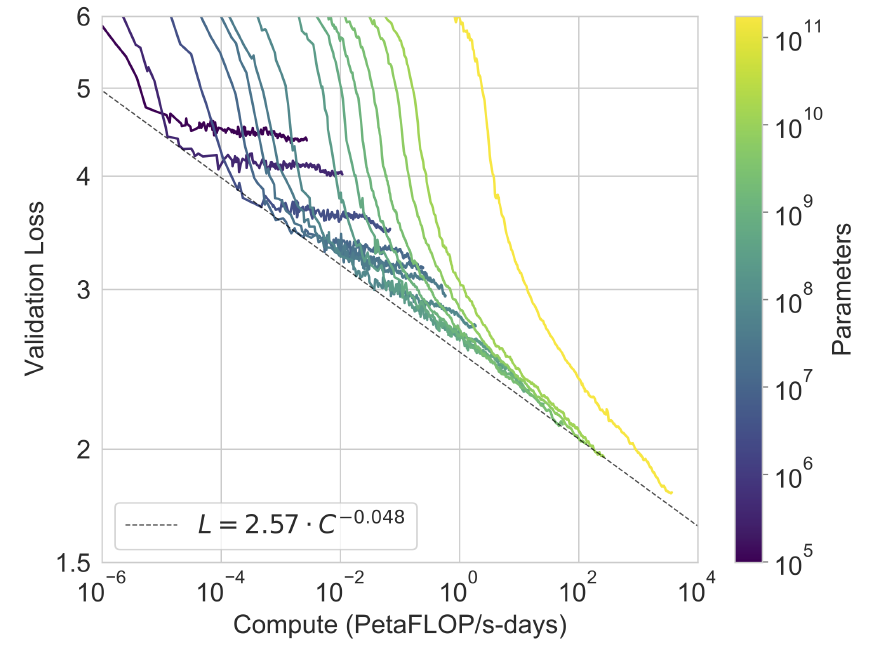
3.3 验证 L 与 C 的关系是否正确

这一步很重要，因为不是只得出类似上图3 L=2.57 \cdot C^{-0.048} 就能证明自己得到的曲线满足Scaling Laws了。这就要用到3.1中 C\sim6ND 这个公式了。因为我们知道， C\sim6ND 这个公式的成立和模型是否训练没有关系，即使模型没有被训练，也应该满足这个关系。

因此，我们可以找到 L=2.57 \cdot C^{-0.048} 与图3中曲线的交点（每条曲线一个交点就行），然后找到曲线中交点对应的计算量 C 、模型参数 N 以及此刻训练的tokens数 D 。

训练过程中，需要多保存一些checkpoint，交点的checkpoint不一定保存了，可以找临近的checkpoint。

拟合计算量 C 、模型参数 N 以及计算量 C 和训练的tokens数 D 的关系，结果如下图所示（ 图3和图4 没有直接关系，只是为了说明情况 ）

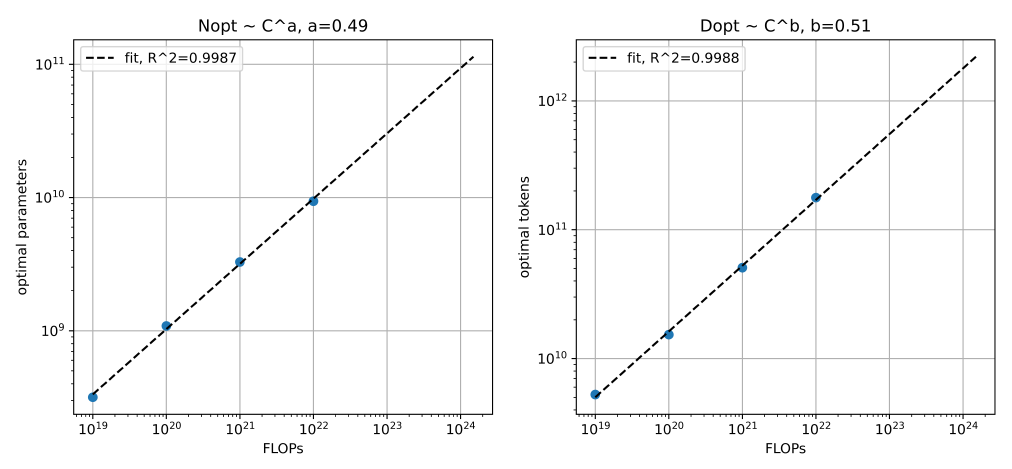
通过拟合计算量 C 、模型参数 N 的曲线，以及计算量 C 和训练的tokens数 D 的曲线，观察结果是否满足 C\sim6ND 。比如图4中 N=1/6\times C^{0.49} , D=C^{0.51} ，两者相乘正好满足 C\sim6ND 。

由此，可以说明图3中的模型性能与计算量的关系是正确的。可以继续下一步的工作。

失败了怎么办？模型的性能与模型参数、数据量是强相关，但是与训练方法、数据质量等也是相关的！

4、怎么用Scaling Laws

从图3和图4分别得到了模型性能与计算量的关系、计算量与模型大小的关系、计算量与训练的tokens之间的关系。那么现在我们有两个问题需要解决：

• 预训练的模型在评估集上（验证集损失上）的性能是多少？
• 达到该性能至少需要多少tokens？

针对这两个问题，我们可以通过模型性能与计算量的关系以及模型大小与计算量的关系直接计算出模型大小与性能的关系（如图5所示的类似关系 图只是一个参考，图4和图5没有关系 ）。这样就可以直接通过具体的模型大小，得到模型在该规模下的具体性能（不考虑训练所需的tokens）。

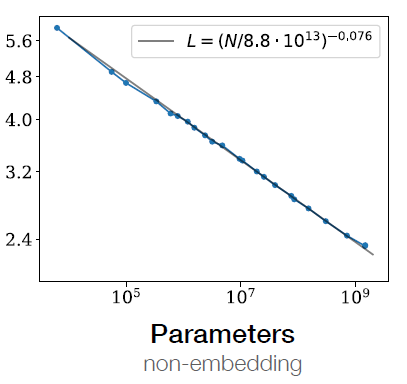
性能不仅仅可以是损失值，也可以是评估集上的具体指标。

如果达到我们的期望，我们可以考虑第二个问题。我们可以通过模型性能与计算量的关系以及训练tokens数与计算量的关系直接计算出训练tokens数与性能的关系（如图6所示的类似关系 图只是一个参考，图4和图6没有关系 ），进而求出训练所需的tokens数。

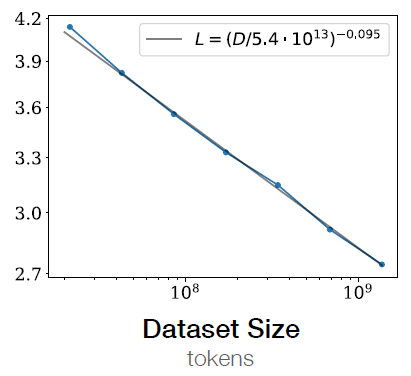
这里还有几个延伸的结论 [1]：

• 当同时增加数据量和模型参数量时（比例增加），模型表现会一直变好。当其中一个因素受限时，模型表现随另外一个因素增加变好，但是会逐渐衰减；
• 当我们对模型在与其训练数据分布不同的文本上进行评估时，结果与在训练验证集上的结果强相关，损失值大致保持一个常数偏移量。换句话说，转移到不同分布的数据上会带来一个常数惩罚，但整体上的改善与在训练集上的表现大致一致。
• 当计算量固定（比如固定要进行n次浮点计算）而数据规模和模型参数量不固定时，性价比最高的计算方式是训练大模型而不是小模型，即使大模型最终到不了收敛状态而小模型能收敛。
• 当计算量增大时，最高效的训练方式是用大模型，提高batch，并且相应的扩大少量数据。

5、引用

[1] Kaplan J, McCandlish S, Henighan T, et al. Scaling laws for neural language models[J]. arXiv preprint arXiv:2001.08361, 2020.

[2] OpenAI. GPT-4 Technical Report. arXiv:2303.08774, 2023.

[3] Anil R, Dai A M, Firat O, et al. PaLM 2 Technical Report[J]. arXiv preprint arXiv:2305.10403, 2023.

[4] Brown T, Mann B, Ryder N, et al. Language models are few-shot learners[J]. Advances in neural information processing systems, 2020, 33: 1877-1901.