时间序列分析预测未来Ⅱ SARIMA
上期讲了理论部分,这期结合代码看看如何做预测,并与预测结果进行比较。
一、导入数据及所需的package。
import matplotlib.pyplot as plt
import numpy as np
from dateutil.relativedelta import relativedelta
import datetime
import time
import pandas as pd
import statsmodels.api as sm
from statsmodels.tsa.stattools import acf
from statsmodels.tsa.stattools import pacf
from statsmodels.tsa.seasonal import seasonal_decompose
df=pd.read_excel(r'D:\weather_forecast\wind.xlsx',index_col=u'YM')
表格包含两列,一列为时间,一列为我们的变量,时间为每个月第一天,也就是我们的时间序列是每个月一个数据,将时间那一列设置为index(也可以使用pandas.DataFrame.set_index ()来实现)。然后简单查看一下这个时间序列的图像,可能潜在哪些趋势:
df['data_list'].plot(figsize=(12,8),title="Daily Wind",fontsize=14)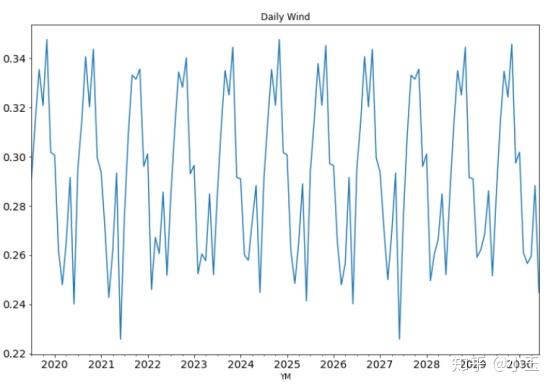
可以看出这列时间序列存在很明显的周期性,且以年为周期。
二、 使用seasonal_decompose查看时间序列概况
decomposition=seasonal_decompose(df['data_list'],freq=12)
fig=plt.figure()
fig=decomposition.plot()
fig.set_size_inches(12,6)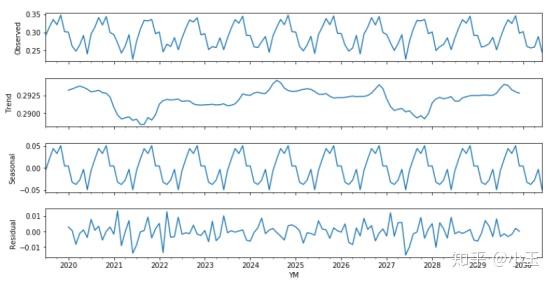
上图使用了移动平均来进行季节性分解。第一个小图observed就是我们观测到的实际值,和最初我们用简单画出来的图像其实是一样的,只是更扁平了,下面第二个图Trend可以看到它整体的变化趋势,然后第三个seasonal是整个序列表现出来的季节性部分,第四个residual是残差。
statsmodels.tsa.seasonal.seasonal_decompose( x , model =‘additive’, filt =None, period =None, two_sided =True, extrapolate_trend =0)
接下来对 seasonal_decompose的参数和用法 做一个详细的介绍。
x : 你要分析的序列。
Model : 第二个参数model 有两种形式。
使用下图来举例:
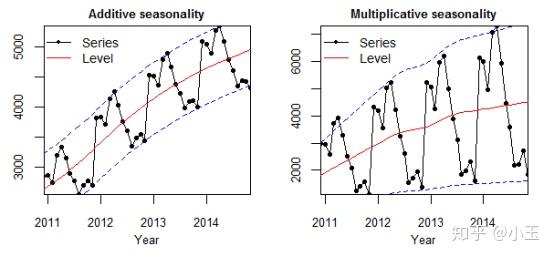
Level : 序列中的平均值。
Trend : 在序列中增加或减小的值。
Seasonality : 季节性表示这个序列中短期周期的重复出现。
Noise : 序列中的随机变量,其实就是整个序列减去趋势和季节性所剩下的残差。
左图为 additive model ,相加模式,它的季节性变化的幅度是独立于时间轴的。中间的红色线为均值,时间序列中每个时刻的值用黑色的点表示,这些黑色的点用公式表示如下:
y(t) = Level + Trend + Seasonality + Noise
在上面四个因素中,他们不互相作用,而是互相区别,直接相加来影响y值。在相加模式下,它在时间轴上是线性的,随着时间的改变是一致的。在这种情况下,线性的周期性有相同的幅度和频率。
右图为 multiplicative model , 相乘模式。
在这种模式中,趋势、季节性和噪音成分是相乘的。它是非线性的,可以是指数形式(exp),多次方的形式。可以用如下公式表示:
y(t) = Level * Trend * Seasonality * Noise
不同于相加模式,随着时间的推移,相乘模式表现出增长(下降)的幅度或者频率。
Filt : 过滤参数,用来过滤掉季节性成分(seasonal)和趋势成分(trend)。可以设置你自己的过滤矩阵,也可以直接设置该参数等于None(default)。当Filt设置自定义为None时,里面代码会根据你的period给你一个Filt矩阵,因为这个在计算时是必须要有的。
当不设置filt参数时,即filt=None时,period为偶数时:
filt=np.array([0.5]+[1]\times(period-1)+[0.5]
当不设置filt参数时,period为奇数时:
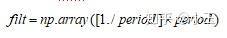
过滤矩阵确定下来后,过滤时所使用的具体移动平均方法,由two_sided的参数决定。
period : 就是周期。
Two_sided :过滤中使用的移动平均(moving average)方法。如果为True, 那么使用的是中心移动平均,就是你计算完移动平均之后,把平均值放在所计算的周期的中间时刻,类似于pandas.rolling_mean(center=True)。如果为false,那么仅用于过去值。
Extrapolate_trend: int or ‘freq’在计算trend的时候,会留有空缺值,这个参数的设置就是判定是否要剥离两端的,或者一端的NaN value,使用前后的效果对比图如下:


了解完它的各个参数,下面看看计算seasonal_decompose中observed, trend, seasonal residual这四个结果的计算。
Observed =x
trend 的计算(仅限extrapolate_trend=0时,因为不等于0时,会把NaN值给剥离掉,还需要考虑到two_side参数):
Tip:此trend非彼trend,注意到这里的trend=上面提及的level+trend,之前提及到的trend是非常纯粹的trend,周期内的平均值是被剥离掉的,它只是表述一个变化趋势。
n_filt: 过滤器的长度,
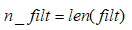
当two_side=False时,nside=int(two_side)+1=1
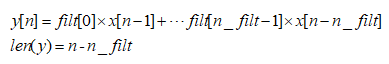
写简单一点:
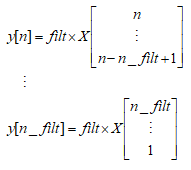
X即为Seasonal_decompose中第一个参数x输入的矩阵,n为长度,因为List是从零开始的,所以在官方文档中使用的是[n-1],我列的矩阵运算中,n仅代表位置,从上面可以看到当获取X值得位置是从1到n_filt时,y最后一个有数值的位置是n_filt,小于n_filt的位置的y得到的是空值NaN。所以y与x相比较还是缺少了n_filt-1个值。上面提到过的我们的数据为以年为周期性变化,一年有12个月,那么period=12,为偶数,所以得到我们的过滤矩阵如下:
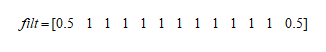

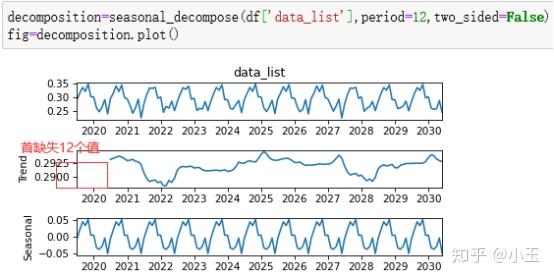
所以得到的trend它会比x少了n_filt-1,即少了12个数值,从下图可以看到前面少了12个值。
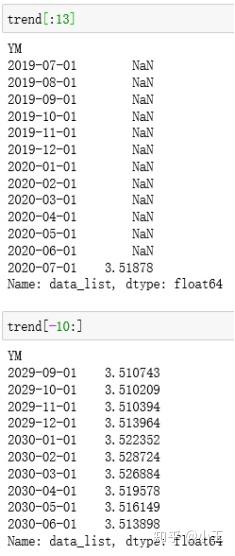
当two_side=True,时,nside=int(two_side)+1=2
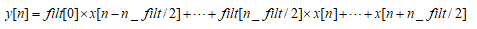
因为这里面n_filt为奇数,在代码部分操作为前后留(n_filt-1)/2个单位的缺失值。
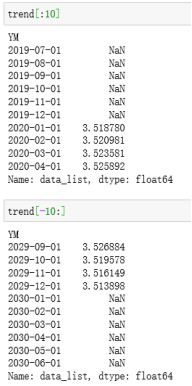
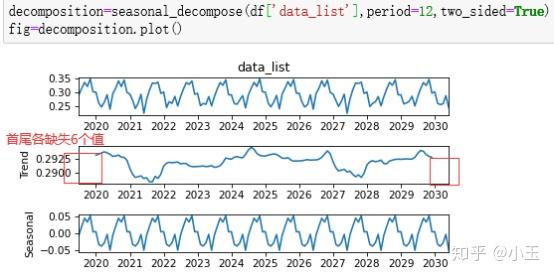
不用太纠结这个,对参数和结果的判定没啥影响。使用convolution_filter也可以计算出上面的结果,你看我手动算的当two_side=True时,和上面那个two_side=True是不是长得一样。
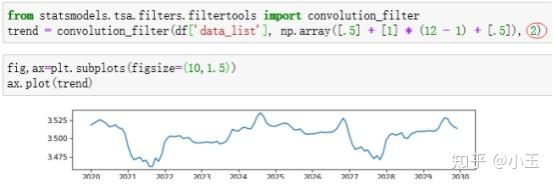
计算完trend,下一步计算seasonal。
seasonal 的计算(需要考虑到model的参数):
在model=additive,加性模式下:先去掉trend,我们把去掉trend之后的叫detrended。detrended = x-trend然后在每个周期的某一时刻求平均值,第一个周期的第一时刻一直加到最后一个周期的第一个时刻再除以周期数即为周期中的第一个时刻的值,以此类推,所有的detrended的值平均之后,可以大致成为我们的季节性成分,但是在此之前需要做出一定的调整,以使得他们在每个周期里面相加为零,这个调整方法其实很简单哈,在前面求得平均的基础上再减掉周期内的平均值就可以得到了,其实大致就是一个向下平移的过程,然后就得到我们的seasonal component,如下图,看到其均值为零,周期性在0上下震荡。

在model=mutiplicative,乘性模式下:也是去掉trend,这里去掉trend的方式不同于additive, 我们把去掉trend之后的也叫做detrended, detrended=x/trend, 相除而不是相减,这里面计算seasonal的方式与在additive模式下类似,但是调整方式不一样,这边不再是减去平均值,而是除以,所以这里也不再是0附近震荡,而是在1附近,如下图:

resid 的计算:
Model=additive 加性模式:Resid=x-trend-seasonal
Model=mutiplicative 乘性模式:Resid=x/seasonal/trend03测试平稳性(stationarity):
三、 测试平稳性
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics:
rolmean=timeseries.rolling(window=12).mean()
rolstd=timeseries.rolling(window=12).std()
#Plot rolling statistics:
fig=plt.figure(figsize=(12,8))
orig=plt.plot(timeseries,color='blue',label='Original')
mean=plt.plot(rolmean,color='red',label='Rolling Mean')
std=plt.plot(rolstd,color='black',label='Rolling std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show()
# Perform Dickey-Fuller test:
# Dickey-Fuller test is used to determine whether a unit root (a feature that can cause
# issues in statistical inference) is present in an autoregressive model.
print('Results of Dickey-Fuller Test:')
dftest=adfuller(timeseries,autolag='AIC')
dfoutput=pd.Series(dftest[0:4],index=['Test statistic','p-value','#Lags Used','Number of Obervations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value(%s)'%key]=value
print(dfoutput)statsmodels.tsa.stattools.adfuller( x , maxlag =None, regression =‘c’, autolag =‘AIC’, store =False, regresults =False)
DF unit root test; ADF单位根验证。
X : array_like, the data series to test, 要测试的数列Maxlag:测试中的最大滞后阶数。
Regression : 回归中所包含的常量和趋势次方,该参数取值范围为{“c”,”ct”,”ctt”,”nc”},各值含义如下:
“c” : 仅包含常量(Regression参数的默认值)
“ct” : 包含常量和趋势
“ctt” : 包含常数,线性和二次趋势
“nc” : no constant, no trend. 不包含常量,不包括趋势。
Autolag {“AIC”,”BIC”,”T-stat”,None}这个方法用来决定需要滞后(lag)的阶数。
滞后阶数的确定一般有两种方法:
参数为T-stat时:取一个较大的滞后(比如说:maxlag),然后逐步缩小直到滞后阶数对应的系数显著;
参数为AIC或BIC时:用AIC或BIC准则,选取最小信息准则(Information Criterion)。
参数为None时:使用maxlag所致指定的滞后阶数。
浅析一下AIC,BIC和T-stat:
AIC : akaike information criterion,赤池信息量准则
The Akaike information criterion (AIC) is an estimator of out-of-sample prediction error and thereby relative quality of statistical models for a given set of data.–wiki
AIC estimates the relative amount of information lost by a given model: the less information a model loses, the higher the quality of that model.–wiki
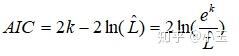
k :未知参数的个数,用来衡量模型的复杂度,参数越多模型越复杂。
L :模型中似然函数的极大值。
赤池信息量准则让你在拟合你数据时,并且不出现过拟合的情况下,来判断你的模型的好坏。当模型复杂度提高时,及k值增大时,似然函数L也会增大,在k值相对较小的情况下,k值的增大对L的增大有明显的作用,这个过程,AIC值是在减小的,当L增大到一定的程度,L随着k值增大而增大得不那么明显了,此时AIC的值会随着k值的增大而增大。对于单个模型来说,不能看出该模型的好坏,只有在使用相同数据下,与其他模型的AIC得分的对比情况下,才能被看出。
比较两个模型的AIC scores
假设我们有两个模型,其中k(number of estimated parameters) 分别为k1和k2,AIC得分分别为AIC1,和AIC2。假设AIC1<AIC2,也是就说模型1要比模型2好,那模型2到底有多糟糕呢,我们用下面的公式来衡量:
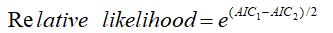
当这个模型的AIC得分比较低时,那么这就意味着这个模型在拟合数据集和避免过拟合之间做到了很好的平衡。
BIC :Bayes Information Criterion 贝叶斯信息准则
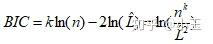
L : the maximized value of the likelihood function for the estimated model,
x : the observed data
n : the number of data points in , the number of observations, or equivalently, the sample size; 就是你有多少行数据
k : the number of parameters estimated by the model. If the estimated model is a linear regression, k is the number of regressors, including the intercepts.
和AIC类似,这里也是追求最小值,但是可以看出BIC对模型复杂度惩罚更严重(k值对information criterion值的影响更大)。
t-stat
In statistics, the t-statistic is the ratio of the departure of the estimated value of a parameter from its hypothesized value to its standard error. It is used in hypothesis testing via Student’s t-test. The T-statistic is used in a T test determine if you should support or reject the null hypothesis. --wiki
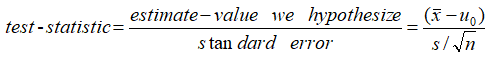
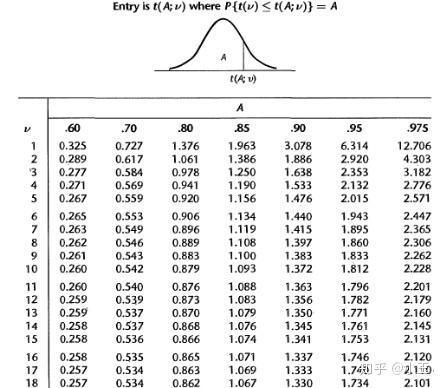
通过t值再根据自由度,可以找出对应confidence interval的值。
Store :bool, 如果为True,则另外返回adf统计信息的结果实例。默认值为False。
Regresults :bool,optional, 如果为True, 则返回完整的回归结果。默认值为False。
statsmodels.tsa.stattools.adfuller返回的值:
ADF : T检验,test statistic, 测试统计
P-value : P值,float, MacKinnon值。
Usedlag : int,最终使用的滞后阶数。
NOBS : int, 用于ADF回归和计算临界值用到的数据量,我们原来有132行,在前面的运算中少了12行(一个周期),所以最后一共用120行用于ADF回归。
Critical value: dict, 置信概率分别为1%,5%,10%的临界值。
Icbest : float, 如果autolag 不是None, 则最大化信息标准(IC)。
Resstore : ResultStore, optional, 一个结果附加在属性上的dummy(非0即1) 类。
df['first_difference']=df['data_list'].diff(1)
# difference it, subtract the previous value from the current value
test_stationarity(df['first_difference'].dropna(inplace=False))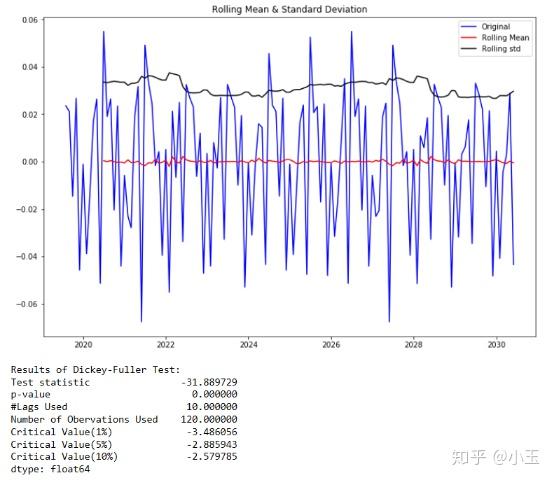
得到上一篇所提及的结果:
1.从图像上判断:一个平稳的时间序列在图形上往往表现出一种围绕其均值不断波动的过程。而非平稳序列则往往表现出在不同的时间段具有不同的均值。由上图可以看出其移动平均(moving average)围绕零波动,rolling mean大致都在零附近。
2.ADF的结果上看,这里 P 值几乎为零,小于给定的显著水平(confidence levels)0.05,所以我们这里可以拒绝这个 null hypothesis,这个原假设是数据是非平稳的,那么我们的结果告诉我们它拒绝承认这个数据是非平稳的,那么也就是说这个数据是平稳的。
四、确定模型及模型参数数据稳定之后,下一步,选择我们需要的模型及参数:
AR:Auto Regressive Model 自回归模型
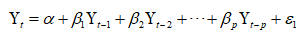
MA: Moving average 移动平均模型
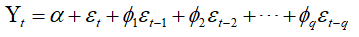
ARIMA(p,d,q): Auto regressive integrated moving average
ARIMA整合了AR和MA,整合的方式如下:
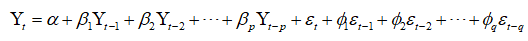
换句话来说:
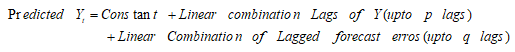
p : Linear combination lags of Y;order of the AR term.
q :Linear combination lagged forecast errors; order of the MA term.
d : order of differencing (d) in ARIMA model to make the time series stationary.
SARIMA : Seasonal Autoregressive Integrated Moving Average.
SARIMA比ARIMA多了一个季节性。
参数的确定:
d :差分的次数,这里注意要避免过差分(over-difference),一般你找到某阶数差分后已经平稳了,你再增加差分的次数,它也是平稳的,因为差分它是一个后面项减前面项的过程,那么这里面得到数列会比差分之前少一个数值,几阶差分就少几个。一旦差分平稳之后就不需要再继续差分下去了,那么这个d值就等于这个初次达到平稳的差分次数。差分的过程如下:
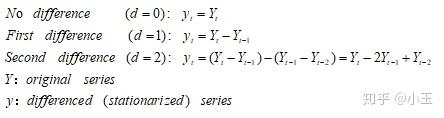
关于p和q参数,p和q的选择,需要根据ACF和PACF的结果来判断。
p 值:
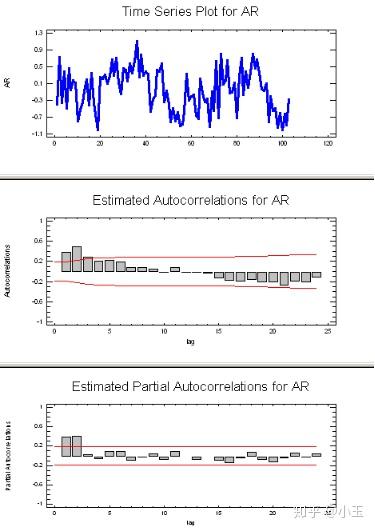
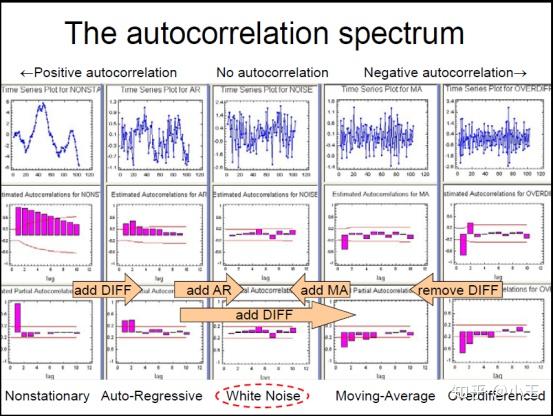
上图的信息表现出AR信号,判断方法:在上面的第二个图中(ACF)均值-反转,逐渐递减(通常在lag1是为正,图中横坐标为lag),在上面的第三个图中(PACF),仅有两个峰,所以AR对应的参数p值为2,AR(2).
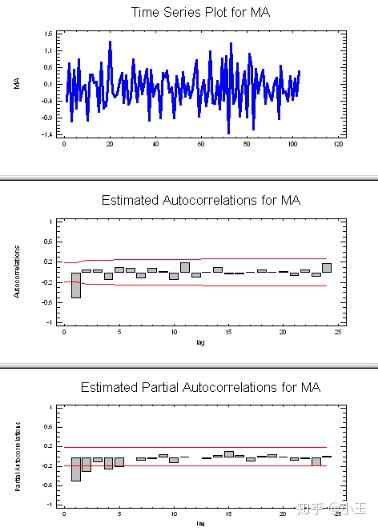
q 值:上图的信息表现出MA信号,MA信号的判断:看起来像噪音,ACF中递减很突然,通常在lag1时为负值,而在PACF中表现为逐渐递减。因为在ACF中只有一个峰,所以这里的MA的参数q值为1,MA(1)。
添加参数的效果大致如下,其目的是为了达到White Noise:
fig=plt.figure(figsize=(12,8))
ax1=fig.add_subplot(211)
fig=sm.graphics.tsa.plot_acf(df['first_difference'].iloc[13:],lags=20,ax=ax1)
ax2=fig.add_subplot(212)
fig=sm.graphics.tsa.plot_pacf(df['first_difference'].iloc[13:],lags=20,ax=ax2)
# as we can see from following figure, noisy pattern, sharp cutoff in ACF(usually negative at lag 1), gradual decay in PACF.
# Here the signature is MA(1) because of 1 spike in ACF.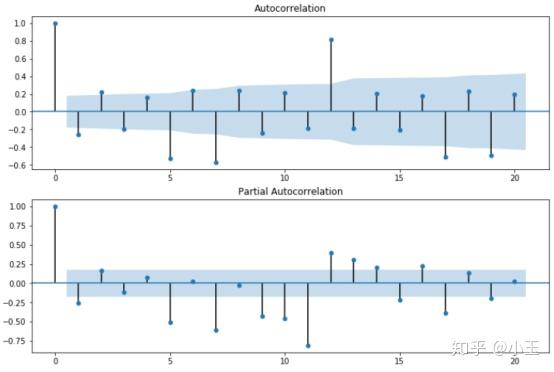
上图为我们的数据运行的结果,在第0个lag时都为正值,在PACF中第一个lag为负值,ACF中第一个lag也是负值,且只有一个峰,所以我们这里p=0,q=1,又因为是一阶差分,所以d=1,那么关于ARIMA的模型已经确立,ARIMA(0,1,1)
然后我们加上季节性这部分SARIMA(p,d,q)x(P,D,Q):
需要引进三个新的参数P,D,Q:
P= number of seasonal autoregressive terms;
D=number of seasonal differences
Q=number of seasonal moving-average terms
将非季节性和季节性差分结合起来使时间序列稳定:
Seasonal 部分参数的确定:
关于D:
从上面的公式中可以看出,d是序列中每个时刻的差分,而D是每个周期的差分,所以这里面D从来都不会超过1,虽然2个周期也是序列的周期,但是不是最小周期。
关于P:
在ACF中,在lag s的地方有峰,且为正值,在PACF中在lag s的地方有正峰,回到上面那个图,我们的周期s=12,在ACF和PACF在lag 12的时候均有一个正峰,那么SAR=1,P=1。
关于Q:
在ACF中,在lag s的地方有峰,且为负值,在PACF中在lag s的地方有负峰,那么SMA=1,显然这种情况和我们上面的情况不符合,所以我们这里SMA=0,Q=0。到这里的话,我们的模型参数已经确定完成SARIMA(p,d,q)(P,D,Q)=SARIMA(0,1,1)(1,1,0), s=12。下面我们把参数放进模型中进行计算。
五、建立模型并预测
train=df[:100]
test=df[100:]把dataframe分成了两部分,一部分用来训练模型,一部分用来测试结果。
mod=sm.tsa.statespace.SARIMAX(train['first_difference'],trend='n',order=(0,1,1),seasonal_order=(1,1,0,12))
results=mod.fit()
print(results.summary())由上面的代码可以看到,使用的是sm.tsa.statespace.SARIMAX,里面的order和seasonal_order参数上面讲过了,trend这里和addfuller中的regression里的字母含义类似:
Trend: str{‘n’,’c’,’t’,’ct’} or iterable, optional.
‘c’: a constant, 一个常量。
‘t’: linear trend with time, 包含随时间线性变化的趋势。
‘ct’:既包含常量也包含线性关系,同时具备上述两者。
‘n’:什么也没有包括,default value是n。
下面我们来看看模型结果:
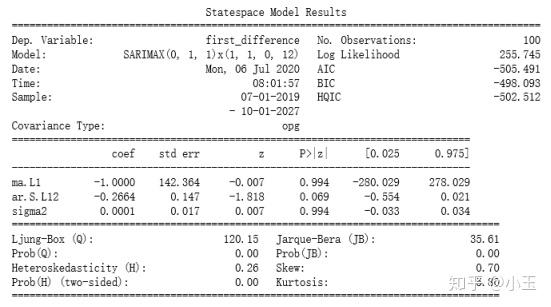
然后开始预测:
test['forecast_first'] = results.predict(start = 100, end= 132, dynamic= True)
test[['first_difference', 'forecast_first']].plot(figsize=(12, 6))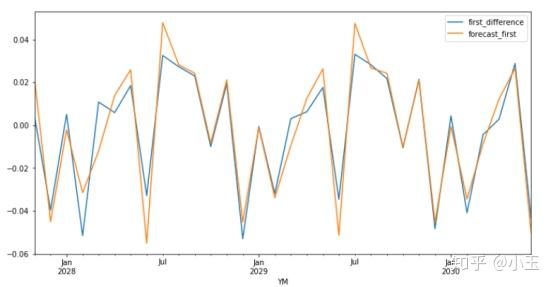
这部分没有放入训练的数据和预测的结果重叠得还可以,需要注意的是这个是一阶差分后的预测结果y,最后我们还需要把结果还原成Y。那么一个个加上差分就可以了。具体操作如下:
x, x_diff = test['data_list'].iloc[:], test['forecast_first'].iloc[:]
C=[]
