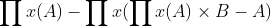1.除法
(1)概述
除法操作一直是关系代数里面比较难理解的一个知识点,下面我将用一个简单的例子先阐述一下他的原理,让大家对他有个初步的认识。
(2)引例
S
|
属性 lesson
|
属性 name
|
|
语文
|
sam
|
|
语文
|
peter
|
|
语文
|
lucy
|
|
数学
|
sam
|
|
数学
|
lucy
|
|
英语
|
sam
|
|
英语
|
peter
|
S1
这种情况下,S/S1的结果是什么呢答案如下
S/S1
再来一个列子
S2
S/S2的结果是什么呢
S/S2
最后一个例子
S3
答案相信大家已经知道答案了
S/S3
这是我能想到的一个应用除法最贴切的例子,就是怎么筛选出这几个同学都选过的课程呢?你要是不太懂得关系运算,这个查询可能做起来就很费尽,你可能会写一个N个同学嵌套的查询,但是要是求一个班同学的查询,那就嵌套了几十个select,那个效率明显不能满足我们的需求。(可能有的人还不知道怎么嵌套,说一说思路把,就是把一个同学所有选的课都选出来,然后和第二个同学对比,求出两个人公共的课程,再把结果和第三个人求公共课,以此类推,就可以求解出所有人公共选择的课程,说到这里大家有没有感觉到,这其实和编程的算法有点类似,刚刚的思路就是暴力求解,而我们的除法操作就是比较优秀的算法)
(3)思路以及通用公式
咱们还是以选课的例子来讲解除法的思路:
首先,我们得把学生,课程L,学生S和课程的一一对应L_S想象成三个集合,然后:
1.先把所有课程和学生作笛卡尔积得到LS(就是建立所有课程和所有学生一一对应的关系,通俗一点就是让每个学生选所有课程)
2.再把刚刚建立的新集合LS和L_S作减法(就是把两个集合作比较只留被减数LS所特有的元组),通俗的说就是找到那些我们期望的人没有同时选择的课。
2.然后吧这些课投影出来,再与之前所有课程做减法就得到了我们期望的结果
通用公式如下:
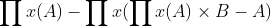
其中A相当于我们的大表S,而B相当与S2其中π操作为投影操作而x为投影条件。
(4)总结:
整个除法的抽象过程就是,先找到被除数那个大集合从中获取我们需要属性的全集,这个通常就是一个带distinct的查询就能解决,然后吧这个结果与除数的集合做笛卡尔积,然后再与原来的大集合做减法,这一步得到的就是那些不同时包含我们除数元组的期望属性,然后再与之前所求的所有属性做减,就得到我们期望的结果。这个过程的思想就是一个先求补集的思想,以为我们需要求同时包含这几项的另外一个属性值这就相当于逻辑与操作,直接做相对于复杂,我们把它转化为集合的运算过后,就容易多了。。
(5)除法运算在嵌套查询的应用:
一般来说嵌套查询就类似与我们平常编程的嵌套循环,算法分析的时候,往往嵌套越多相对应算法的性能就越差,因为当我们操作的集合足够大的时候这个时间会按幂函数增长,大到一定程度就会大大降低用户对于服务的体验。
应用场景:
要从一个大表里面找出同时包含所有我们检索到的多组元组的元组。
方法分析:有时候这个元组并不是包含一个属性,我们就假设有m个属性,而大表中有n个元组,小表有s个元组,同时我们期望的属性有K组通常K<=n,而m是远远小于n的,所以我们开始来分析两种查询的时间复杂度
嵌套:我们要为小表没一组元组对大表进行匹配这个过程的时间复杂度为:O(m*n),而下一步是进行嵌套就相当于做s次前面的匹配过程,时间复杂度为O((m*n)^s)。
然而对于我们的除法操作:
先找出K复杂度为O(n),而做笛卡尔积复杂度为O(K*s),而相减O(n*k*s)最后一个减法就可以忽略不计了,整体复杂度为O(n*k*s)
整体来说要是小集合只有一两组元组,那完全可以用嵌套查询,但是要什么四五六七八九,那个查询次数将成为天文数字,除法操作将成为不错的选择。
(6)除法操作的MySQL实现:
一般情况下使用这条语句就能实现整个过程,select distinct lesson from ( select distinct lesson from SS,S2) as all_les where not exists (select * from SS where all_les.lesson = lesson and all_les.name = name);
但是笛卡尔积过后的表是无法保存的,as all_les在mysql是无法识别的,所以这种方式是不可行的。所以只能先把所有的课选出来存在临时表中,
create temporary table les (select distinct lesson from SS);
然后再把笛卡尔积的结果放在另一张表中,
create temporary table all_les (select * from les,S2);
然后就可以进行除法操作了
select distinct lesson from all_les where not exists (select * from SS where all_les.lesson = lesson and all_les.name = name);

第一个是SS,就是我们之前提到的相关连的表即被除数,第二个S2即除数,第三个就是除法的结果,只有数学没有被sam和peter同时选择。数据库除法实现