探秘双重机器学习：因果推断新视角，揭开模型参数偏误之谜！

link之家

链接快照平台

输入网页链接，自动生成快照
标签化管理网页链接

相关文章推荐

还单身的山寨机 · 连云港市侨联· 5 天前 ·

踢足球的甘蔗 · 北京科技大学图书馆-通知公告· 2 月前 ·

热心肠的山羊 · 末世感叩击：《新世纪福音战士》的文字世界_Use· 1 年前 ·

大方的沙滩裤 · 【长江EV】长江EV汽车报价-图片-长江EV ...· 1 年前 ·

谦和的墨镜 · 黄冈十四五规划铁路和公路方面的内容出炉了，红 ...· 1 年前 ·

今天给大家分享的内容是双重机器学习知识，双重机器学习是因果推断领域发展起来的较新的研究内容，实现了机器学习和因果推断领域的结合，我们知道机器学习更加注重模型的预测，这在一定程度上会导致参数估计的偏误，双重机器学习在一定程度上纠正了这种偏误，从而实现了机器学习在因果推断领域的研究，对于双重机器学习的知识，我们主要借助于以下两篇论文： Double/debiased machine learning for treatment and structural parameters 和 ddml: Double/debiased machine learning in Stata ，其中第一篇文章是双重机器学习的理论介绍文章，该文章理论知识深厚，数学表达式丰富；第二篇文章是双重机器学习结合了stacking思想在stata中的实现，包含重要的理论知识和代码演示。

因果推断的开始和发展是从传统的计量模型中起步，既然传统的计量模型也可以进行因果推断，那么我们为什么还要发展出机器学习的方法来辅助因果推断呢？学术的发展都是讲究一定的效用和意义的，如果仅仅是换了种方法来实现同样的效果，那么该方法的认可度并不会太高，双重机器学习能够在学术界得到一定程度的认可，那么说明该方法相对于传统方法来说，是具备一定的突破性。

因此我们首先讲一讲双重机器学习在传统模型上面的突破，研究表明传统非参数模型会陷入维度诅咒，也就是说传统非参数模型在高纬数据上得到一个较差的估计量，而机器学习相关的算法是基于数据驱动，因此在高纬和非线性数据关系捕捉性能表现较好，因此使用机器学习的方法可以克服传统模型在维度上的诅咒，在这里我们提一下，计量经济学中的高维和机器学习中的高维的差别，首先，高纬是拥有大量的特征和变量，这个大量是多大我们不知道，但是在计量领域认为数据的维度大于数据的个数就称为高维数据，在机器学习的角度，是对数据量会有一定的要求，因此，仅仅从数据的特征数量来说是很少超过数据量的，高纬的情形不是很普遍，同时我们将特征与特征之间的关系或者高次方项，我们统一考虑为交互关系或者非线形关系，机器学习关注预测，因此在实际的建模过程中我们并不会特意构造类似的特征数据做为新的特征，但是传统的计量模型中注重模型的解释，因此，特征与特征的交互，特征的高次方、对数关系就显得尤为重要，我们在实际回归模型构建过程中经常会人工手动构建出一些非线形的特征来考虑对变量的影响，因此在论文中会出现特征随着数据量的增大而不断扩张，从而出现在传统模型中存在的维度诅咒，随着数据的不断增大，数据之间的关系也变得复杂，尽管原始的特征没有变化，但是由于数据之间的复杂关系，因此在传统模型中就必须考虑到特征之间的非线形关系等，例如：交互项、高次方等，然而机器学习在处理这些问题具有一定的优势。

OK，我们已经解决了我们提出的第一个问题，使用机器学习来进行建模不就可以了吗？如果是这么简单就好了，第二个问题出现了，既然这么好，那么为什么机器学习出现之后，传统经济模型在因果推断领域生生不息，大家可以去了解该方面的文章，因果推断还是传统模型居多，说明什么？机器学习在因果推断领域会有一定问题，当然这一方面我还没有过多的探究，其中一个方面的话，我个人认为是“黑盒理论”，机器学习缺乏可解释性，尤其是在经济领域，在一个复杂的问题研究，可能也需要较为复杂的模型来模拟现实情况才可能得到较为准确的结论，因此，集成模型等复杂模型等使用可能更为普遍，但是确定也十分明显，模型的解释性缺乏，只知道结果，不知道如何产生。第二个方面的话，就想文章中说到的机器学习来研究经济问题是存在偏误的，因果推断注重解释，因此在有限数据的情况下，模型的偏误越小越好，但是机器学习追求泛化能力，因此会要求牺牲训练数据的准确性，来实现泛化能力，如果将机器学习直接使用到参数估计，会参数较大的偏差，并且随着数据量的增大，这个偏差会不断增大的，后续会有公式推导。因此，作者提出了双重机器学习的方法来降低这个偏差，最终得到参数的一致估计。

我们先以半参数模型为例来讲述直接使用机器学习的方法会产生偏差的原理，经典的半参数模型如下：

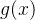其中D是我们的政策或者实验效应变量， $\theta_{0}$ 代表D的参数，也就是我们要估计的变量， $g(x)$ 代表我们要考虑的一系列控制变量，用非参数的形式表示，U是残差。我们可以构建一个机器学习模型 $D\hat{\theta_{0}}+\hat{g_{0}(x)}$ 与目标变量Y进行回归可以得到我们的估计量 $\theta$ ，得到下面公式：

我们将 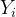$Y_{i}$ 带入，同时乘以 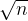$\sqrt{n}$ ，可以得到下面结果：

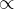显然右边第一部分公式服从正态分布，均值为0，右边第二部分公式为我们估计的量与真实值之间的差距，即偏差 $g_{0}(x)-\hat{g_{0}(x)}$ ，收敛速度为 $n^{-\varphi g}\sqrt{n} \rightarrow \propto$ ,大家应该可以理解，D是一个常数，因此收敛速度取决于 $g_{0}(x)-\hat{g_{0}(x)}$ ,我们假设收敛速度为 $n^{-\varphi g}$ ， $\varphi g<1/2$ ,因此整个表达式是趋近 $\propto$ ，换句话说，随着样本量的不断增大，我们估计的参数 $\hat{\theta_{0}}$ 由于偏差的存在，会越来越偏离我们的真实值。因此作者引入了内曼正交和交叉拟合较好的解决了这个问题，从而使得我们能够得到一致的估计量，引入内曼正交之后，模型变成了

我们求解得到估计量如下：

和上面一样，通过带入即可得到如下分解：

我们可以得到分解出来得到的a仍然是正态分布，均值为0，对于b就是我们得到的偏差项，主要有两部分组成，分别是 $V_{i}=\hat{m_{0}(x)}-m_{0}(x)$ 和 $g_{0}(x)-\hat{g_{0}(x)}$ ，在使用样本分割的情况下，使用辅助样本的情况下， $E(V|X)=0$ ,同时根据切比雪夫不等式，得到

因此根据上面的条件我们分解得到的b项会以概率趋近于0，因此在对样本的进行分割的前提下，使用辅助样本来进行机器学习估计，使用主样本来进行参数估计，我们将会使得残差逐渐减小最终消失，从而得到一致的估计量，这里特别强调了一些要使用样本分割来进行参数估计和机器学习估计，因为如果说使用全样本来进行机器学习和参数估计的话，将不会得到一致的估计并且会产生较大的偏差，在上面公式中的呈现就是U和V存在相关，可能不一定满足均值为0的正态分布，但是如果不使用全样本进行估计，会导致一定效率损失，因此，作者提出的方法是使用交叉拟合的方法，对样本进行多折划分，使用其中的一部分得到机器学习估计量，剩余的样本得到参数估计，对不同选择下的参数估计求均值或者中文数得到最终的估计量。

对于上面辅助模型的构建，作者采用的是内曼正交的思想，具体关于内曼正交相关的知识作者在论文中有所呈现，大家感兴趣可以自行下载阅读，核心的作用就是，第一阶段的估计量的偏差不会对第二阶段估计量产生较大影响，我们对于参数 $\theta$ 的估计可以通过分数函数求期望得到，在传统模型下得到的分数函数为 $\varphi (x;\theta ;\beta )=(Y-D\theta -g(x))D$ ,对分数函数的期望求倒数得：

大家可以看到分数函数的一阶倒数不等于0，说明什么 $\theta$ 的估计对第一阶段的机器学习的估计量很明感， $g_{0}(x)$ 的微小变化也会引起 $\theta$ 估计的变化。我们引入内曼正交之后，分数函数变成了： $\varphi (x;\theta ;\eta )=(Y-D\theta -g(x))(D-m(x))$ , $\eta =(m,g)$ 分数函数期望的一阶导数变成了

也就是说机器学习g估计量误差的微小变化不会影响到最终参数的估计，参数的估计量保持稳定，第一阶段机器学习的估计偏差不会影响到第二阶段OLS参数估计，从而导致第二阶段参数的一致性。以上就是 Double/debiased machine learning for treatment and structural parameters 这篇论文相关的核心思想和理论，本来是想给大家结合第二篇文章进行一个讲解，突然发现也没有什么好讲的了，第二篇文章侧重于双重机器学习思想的实际应用，说明了算法的实际应用流程，并在stata中提供了命令，大家可以查看，我们就说一些比较重要的吧，stata中使用ddml命令需要借助python环境，因为很多机器学习模型都是使用python中scikit-learn中的模型，因此需要安装python和scikit-learn包，大家可以自行安装，这一块可以参考网上资料，安装完成之后在stata中引入python环境即可使用，步骤如下：

输入python search 获取python安装目录，使用python set exec 路径引入python环境，我接着按照论文中给出的部分线形模型使用stacking来进行操作，如果说大家中途有什么其他的问题基本就是包文件没有安装或者版本不适配等。

结果如下：

最后你给大家推荐一篇关于双重机器学习实证应用等论文，网络基础设施、包容性绿色增长与地区差距———基于双重机器学习的因果推断这一篇论文是发表在数量经济技术经济研究上面2023年的文章，还算是比较新的，大家可以借鉴学习，如果说不想去知网下载，可以关注我的公众号“ 明天科技屋 ”，回复数字关键词“ 0005 ”即可获得，上面的两篇文章也会一起发送！希望大家多多关注，并给公众号文章点点赞👍！

DoubleML-R中的双重 机器学习 R包DoubleML提供了的双重 /无偏 机器学习 框架的。它建立在和（Lang等人，2019）。请注意，R包是与基于的python twin一起开发的。 python包也可以在和。文档和维护 R中的功能文档： : 用户指南：： DoubleML当前由和维护。双重 /无偏 机器学习 框架部分线性回归模型（PLR）部分线性IV回归模型（PLIV）互动回归模型（IRM）交互式IV回归模型（IIVM）基于的DoubleML的面向对象的实现非常灵活。模型类DoubleMLPLR ， DoubleMLPLIV ， DoubleMLIRM和DoubleIIVM通过 机器学习 方法和Neyman正交得分函数的计算来实现对有害功能的估计。所有其他功能都在抽象基类DoubleML 。特别是用于估计双重 机器学习 模型并通过随机森林算法（RandomForest，简称RF）一、解决的问题二、解决方法的框架/流程1.基本思想：RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。（即先从节点的属性集合M中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分，一般k远小于M，取k= ）。2、基本的流程：a. 从训练数据中选取n个数据作为训练数据输入，有... 即使使用随机实验数据，DML方法仍然需要考虑一些因素，例如样本大小、特征的选择和处理、模型的选择和调参等。如果实验设计得当，并且随机化合理，那么通过DML训练的模型可以更好地捕捉因果关系，从而获得更准确的效应估计。因此，使用随机实验数据进行DML训练可能会在某些情况下获得更好的效果，但并不是绝对的规律。在应用DML方法时，仍然需要根据实际情况进行数据分析、模型选择和验证，以确保获得准确和可靠的因果效应估计。请注意，实际情况中的数据可能更加复杂，您可能需要根据您的数据和问题来适当选择的模型和参数。地级市2010-2019网络基础设施包容性绿色增长与地区差距基于双重 机器学习 的因果推断含原始数据及计算结果、计算代码、参考文献数据来源：基于上市公司年报、公告数据，中国统计年鉴、及各地区统计年鉴数据的整理计算数据期间：2010-2019 数据范围：全国各地级市参考文献：网络基础设施、包容性绿色增长与地区差距——基于双重 机器学习 的因果推断主要指标：虽然大多数情况下，是给高风险的客户降低额度，但在大数据风控场景下，我们所谈论的好坏客户、风险高低，都是基于概率层面，所谓高风险客户中，大部分都是未来能正常还款的客户。如果我们关心T对Y的影响，首先使用任意 机器学习 算法，通过X拟合T，得到一个T的残差(实际T-预测T)，然后通过X再拟合Y，得到一个Y的残差(实际Y-预测Y)，最后通过线性回归，用T的残差拟合Y的残差，回归的系数即我们想要的无偏因果效应。显然，额度的变动会导致客户的借款意愿的变化——提额会提升客户的借款意愿，降额会降低客户的借款意愿。近年来，研究人员在实证研究中经常使用多通道聚类的抽样数据展开分析：如匹配后的雇主-雇员数据、匹配后的学生-教师数据、观察结果按商店和产品双重索引的匹配数据、以及观察结果按市场和产品双重索引的市场份额数据等。这些数据通常会面临着多维相关性的问题，并不符合独立同分布的性质。并且，如果只在单一层面估计聚类标准误，就会难以兼顾另一层面相关性对结果所造成的偏误。 DoubleML-Python中的双机学习 Python软件包DoubleML提供了的双重 /无偏 机器学习 框架的。它建立在（Pedregosa等，2011）。请注意，Python软件包是与基于的R twin一起开发的。 R包也可以在和。文档和维护文档和网站： : DoubleML当前由和维护。可以将错误报告给问题跟踪器，为。双重 /无偏 机器学习 部分线性回归模型（PLR）部分线性IV回归模型（PLIV）互动回归模型（IRM）交互式IV回归模型（IIVM） DoubleML的面向对象的实现非常灵活。模型类DoubleMLPLR ， Doub 线性模型可以是用曲线拟合样本，但是分类的决策边界一定是直线的，例如logistics 模型区分是否为线性模型，主要是看一个乘法式子中自变量x前的系数w,如果w只影响一个x，那么此模型为线性模型。或者判断决策边界是否是线性的神经网络是非线性的虽然神经网络的每个节点是一个logistics 模型，但是组合起来就是一个非线性模型。此处我们仅仅考虑三层神经网络 2. 计算特征相关性的方法，特征... 然后，通过整合这些决策树的结果，得到对处理效应的估计。该方法允许使用任意的 机器学习 算法进行这两个预测任务，同时保持与最终模型相关的许多有利的统计性质（例如较小的均方误差、渐近正态性、置信区间的构建）。这种组合方法的好处在于，双重 机器学习 可以帮助处理内生性和非线性关系，而因果森林可以提供对处理效应的非参数估计。它们的结合有助于更准确地估计处理效应，并提供对估计结果的统计不确定性的评估。：计算T的残差是正交于变量X的，所以X的作用被剔出了，即此时T的残差独立于X，而Y的残差中剔除了X对于Y方差的影响。原文地址：一只鸟的天空，http://blog.csdn.net/heyongluoyao8/article/details/49408131 在分类中如何处理训练集中不平衡问题在很多 机器学习 任务中，训练集中可能会存在某个或某些类别下的样本数远大于另一些类别下的样本数目。即类别不平衡，为了使得学习达到更好的效果，因此需要解决该类别不平衡问题。 Jason Brownlee的回答：一、背景目前我们能看到因果推断相关的资料更多的聚焦在逻辑方法本身，公式非常繁杂导致较难理解与应用。有的时候虽然看似理解了一些，但是真正应用的时候还是不太清楚什么场景应该选择什么方法。基于此种背景，笔者梳理一些目前业界的通用业务问题场景，按照不同分析场景类型分为四大类，分别对应不同的适用因果推断解决方法，并辅以通俗易懂的语言去解释其原理与案例。当遇到某类问题的时候，我们能快...