[干货]深入浅出LSTM及其Python代码实现
人工神经网络在近年来大放异彩,在图像识别、语音识别、自然语言处理与大数据分析领域取得了巨大的成功。本文将由浅入深介绍循环神经网络RNN和长短期记忆网络LSTM的基本原理,并基于Pytorch实现一个例子,完整代码在文章最后。
获取更多技术干货:
1. 神经网络简介
1.1 神经网络起源
人工神经网络(Aritificial Neural Networks, ANN)是一种仿生的网络结构,起源于对人类大脑的研究。人工神经网络(Aritificial Neural Networks)也常被简称为神经网络(Neural Networks, NN),基本思想是通过大量简单的神经元之间的相互连接来构造复杂的网络结构,信号(数据)可以在这些神经元之间传递,通过激活不同的神经元和对传递的信号进行加权来使得信号被放大或衰减,经过多次的传递来改变信号的强度和表现形式。
神经网络最早起源于20世纪40年代,神经科学家和控制论专家Warren McCulloch和逻辑学家Walter Pitts基于数学和阈值逻辑算法创造了最早的神经网络计算模型。由于当时的计算资源有限,无法构建层数太多的神经网络(3层以内),因此神经网络的应用范围很局限。随着计算机技术的发展,神经网络层数的增加带来的计算负担已经可以被现代计算机解决,各位前辈大牛对于神经网络的理解也进一步加深。历史上神经网络的发展大致经历了三次高潮:20世纪40年代的控制论、20世纪80年代到90年代中期的联结主义和2006年以来的深度学习。深度学习的出现直接引爆了一部分应用市场,这里有太多的案例可以讲,想了解的读者可参考下面的链接:
1.2 传统神经网络的缺陷
本文假设读者已经了解神经网络的基本原理了,如果有读者是初次接触神经网络的知识,这里分享一篇个人觉得非常适合初学者的文章:
1.2.1 传统神经网络的原理回顾
传统的神经网络结构可以用下面这张图表示:
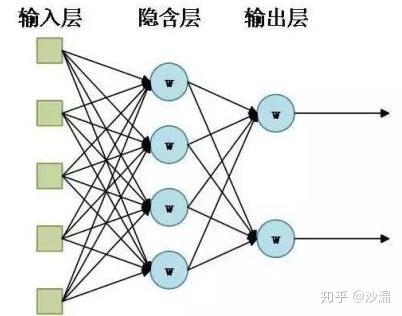
其中:
- 输入层:可以包含多个神经元,可以接收多维的信号输入(特征信息);
- 输出层:可以包含多个神经元,可以输出多维信号;
- 隐含层:可以包含多个神经网络层,每一层包含多个神经元。
每层的神经元与上一层神经元和下一层神经元连接(类似生物神经元的突触),这些连接通路用于信号传递。每个神经元接收来自上一层的信号输入,使用一定的加和规则将所有的信号输入汇聚到一起,并使用 激活函数 将输入信号激活为输出信号,再将信号传递到下一层。
神经网络为什么要使用激活函数?不同的激活函数有什么不同的作用?读者可参考:
所以,影响神经网络表现能力的主要因素有神经网络的层数、神经元的个数、神经元之间的连接方式以及神经元所采用的激活函数。神经元之间以不同的连接方式(全连接、部分连接)组合,可以构成不同神经网络,对于不同的信号处理效果也不一样。但是,目前依旧没有一种通用的方法可以根据信号输入的特征来决定神经网络的结构,这也是神经网络模型被称为黑箱的原因之一,带来的问题也就是模型的参数不容易调整,也不清楚其中到底发生了什么。因此,在不断的探索当中,前辈大牛们总结得到了许多经典的神经网络结构:MLP、BP、FFNN、CNN、RNN等。详细的介绍见以下链接:
神经网络优点很明显,给我们提供了构建模型的便利,你大可不用顾及模型本身是如何作用的,只需要按照规则构建网络,然后使用训练数据集不断调整参数,在许多问题上都能得到一个比较“能接受”的结果,然而我们对其中发生了什么是未可知的。在深度学习领域,许多问题都可以通过构建深层的神经网络模型来解决。这里,我们不对神经网络的优点做过多阐述。
1.2.2 传统神经网络结构的缺陷
从传统的神经网络结构我们可以看出,信号流从输入层到输出层依次流过,同一层级的神经元之间,信号是不会相互传递的。这样就会导致一个问题,输出信号只与输入信号有关,而与输入信号的先后顺序无关。并且神经元本身也不具有存储信息的能力,整个网络也就没有“记忆”能力,当输入信号是一个跟时间相关的信号时,如果我们想要通过这段信号的“上下文”信息来理解一段时间序列的意思,传统的神经网络结构就显得无力了。与我们人类的理解过程类似,我们听到一句话时往往需要通过这句话中词语出现的顺序以及我们之前所学的关于这些词语的意思来理解整段话的意思,而不是简单的通过其中的几个词语来理解。
例如,在自然语言处理领域,我们要让神经网络理解这样一句话:“地球上最高的山是珠穆朗玛峰”,按照传统的神经网络结构,它可能会将这句话拆分为几个单独的词(地球、上、最高的、山、是、珠穆朗玛峰),分别输入到模型之中,而不管这几个词之间的顺序。然而,直观上我们可以看到,这几个词出现的顺序是与最终这句话要表达的意思是密切相关的,但传统的神经网络结构无法处理这种情况。
因此,我们需要构建具有“记忆”能力的神经网络模型,用来处理需要理解上下文意思的信号,也就是时间序列数据。循环神经网络(RNN)就是用来处理这类信号的,RNN之所以能够有效的处理时间序列数据,主要是基于它比较特殊的运行原理。下面将介绍RNN的构建过程和基本运行原理,然后引入长短期记忆网络(LSTM)。
2. 循环神经网络RNN
本章将介绍循环神经网络的基本原理,参考了下文:
以及YouTue上的一个视频:
2.1 RNN的构造过程
RNN是一种特殊的神经网路结构,其本身是包含循环的网络,允许信息在神经元之间传递,如下图所示:

图示是一个RNN结构示意图,图中的 A 表示神经网络模型, X_t 表示模型的输入信号, h_t 表示模型的输出信号,如果没有 A 的输出信号传递到 A 的那个箭头, 这个网络模型与普通的神经网络结构无异。那么这个箭头做了什么事情呢?它允许 A 将信息传递给 A ,神经网络将自己的输出作为输入了!这怎么理解啊?作者第一次看到这个图的时候也是有点懵,读者可以思考一分钟。
关键在于输入信号是一个时间序列,跟时间 t 有关。也就是说,在 t 时刻,输入信号 X_t 作为神经网络 A 的输入, A 的输出分流为两部分,一部分输出给 h_t ,一部分作为一个隐藏的信号流被输入到 A 中,在下一次时刻输入信号 X_{t+1} 时,这部分隐藏的信号流也作为输入信号输入到了 A 中。此时神经网络 A 就同时接收了 t 时刻和 t+1 时刻的信号输入了,此时的输出信号又将被传递到下一时刻的 A 中。如果我们把上面那个图根据时间 t 展开来看,就是:

看到了吗? t=0 时刻的信息输出给 t=1 时刻的模型 A 了, t=1 时刻的信息输出给 t=2 时刻的模型 A 了, \dots 。这样,相当于RNN在时间序列上把自己复制了很多遍,每个模型都对应一个时刻的输入,并且当前时刻的输出还作为下一时刻的模型的输入信号。
这样链式的结构揭示了RNN本质上是与序列相关的,是对于时间序列数据最自然的神经网络架构。并且理论上,RNN可以保留以前任意时刻的信息。RNN在语音识别、自然语言处理、图片描述、视频图像处理等领域已经取得了一定的成果,而且还将更加大放异彩。在实际使用的时候,用得最多的一种RNN结构是LSTM,为什么是LSTM呢?我们从普通RNN的局限性说起。
2.2 RNN的局限性
RNN利用了神经网络的“内部循环”来保留时间序列的上下文信息,可以使用过去的信号数据来推测对当前信号的理解,这是非常重要的进步,并且理论上RNN可以保留过去任意时刻的信息。但实际使用RNN时往往遇到问题,请看下面这个例子。
假如我们构造了一个语言模型,可以通过当前这一句话的意思来预测下一个词语。现在有这样一句话:“我是一个中国人,出生在普通家庭,我最常说汉语,也喜欢写汉字。我喜欢妈妈做的菜”。我们的语言模型在预测“我最常说汉语”的“汉语”这个词时,它要预测“我最长说”这后面可能跟的是一个语言,可能是英语,也可能是汉语,那么它需要用到第一句话的“我是中国人”这段话的意思来推测我最常说汉语,而不是英语、法语等。而在预测“我喜欢妈妈做的菜”的最后的词“菜”时并不需要“我是中国人”这个信息以及其他的信息,它跟我是不是一个中国人没有必然的关系。
这个例子告诉我们,想要精确地处理时间序列,有时候我们只需要用到最近的时刻的信息。例如预测“我喜欢妈妈做的菜”最后这个词“菜”,此时信息传递是这样的:
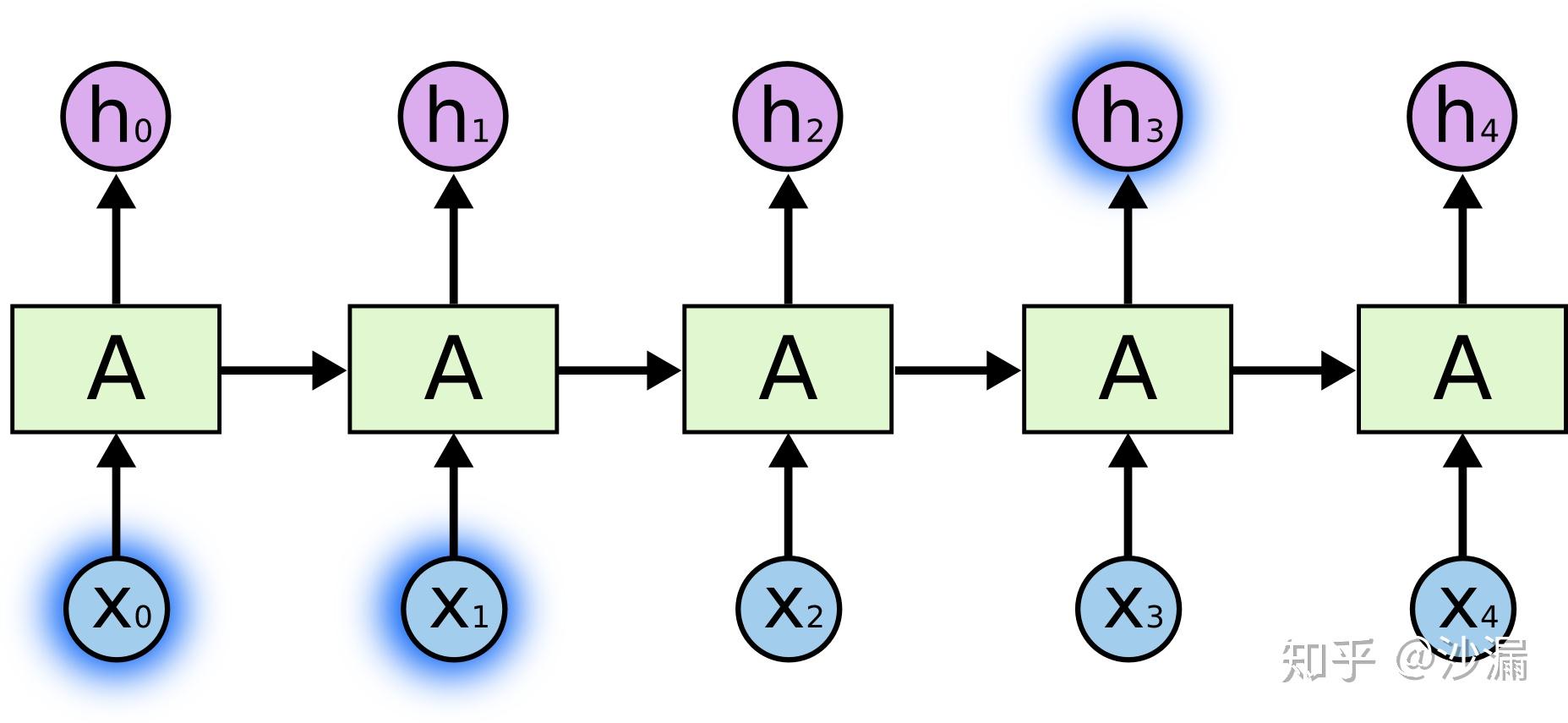
“菜”这个词与“我”、“喜欢”、“妈妈”、“做”、“的”这几个词关联性比较大,距离也比较近,所以可以直接利用这几个词进行最后那个词语的推测。
而有时候我们又需要用到很早以前时刻的信息,例如预测“我最常说汉语”最后的这个词“汉语”。此时信息传递是这样的:
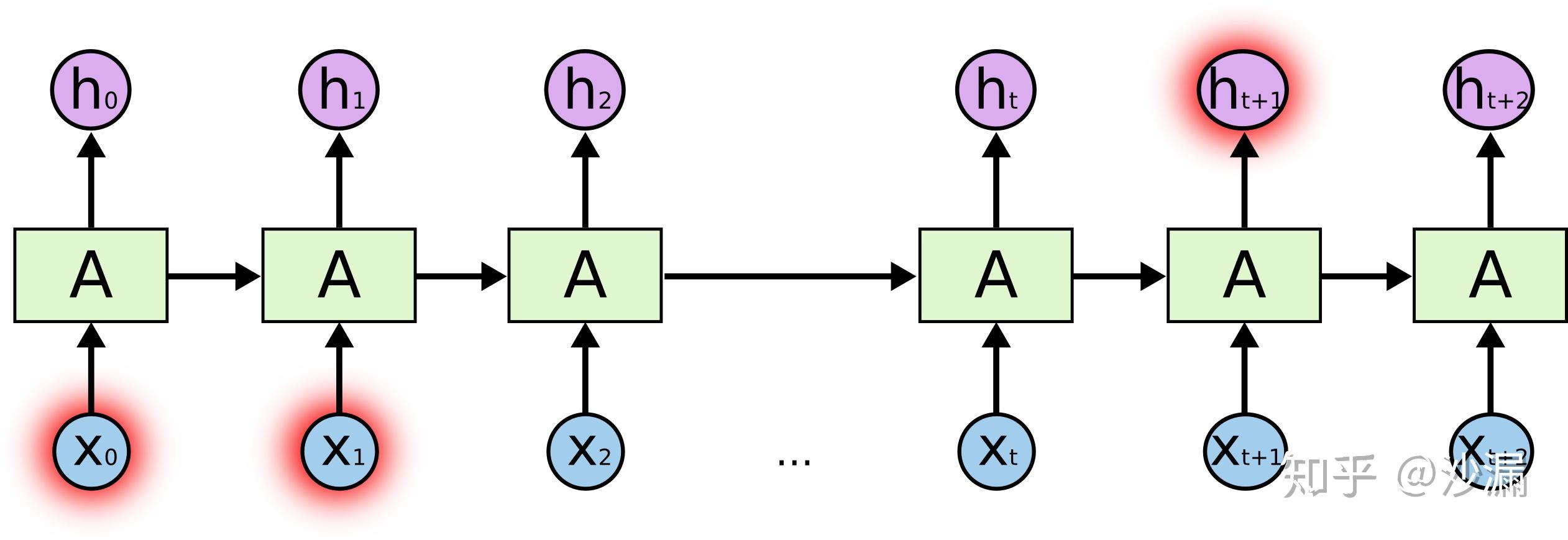
此时,我们要预测“汉语”这个词,仅仅依靠“我”、“最”、“常”、“说”这几个词还不能得出我说的是汉语,必须要追溯到更早的句子“我是一个中国人”,由“中国人”这个词语来推测我最常说的是汉语。因此,这种情况下,我们想要推测“汉语”这个词的时候就比前面那个预测“菜”这个词所用到的信息就处于更早的时刻。
而RNN虽然在理论上可以保留所有历史时刻的信息,但在实际使用时,信息的传递往往会因为时间间隔太长而逐渐衰减,传递一段时刻以后其信息的作用效果就大大降低了。因此,普通RNN对于信息的长期依赖问题没有很好的处理办法。
为了克服这个问题,Hochreiter等人在1997年改进了RNN,提出了一种特殊的RNN模型——LSTM网络,可以学习长期依赖信息,在后面的20多年被改良和得到了广泛的应用,并且取得了极大的成功。
3. 长短时间记忆网络(LSTM)
3.1 LSTM与RNN的关系
长短期记忆(Long Short Term Memory,LSTM)网络是一种特殊的RNN模型,其特殊的结构设计使得它可以避免长期依赖问题,记住很早时刻的信息是LSTM的默认行为,而不需要专门为此付出很大代价。
普通的RNN模型中,其重复神经网络模块的链式模型如下图所示,这个重复的模块只有一个非常简单的结构,一个单一的神经网络层(例如tanh层),这样就会导致信息的处理能力比较低。
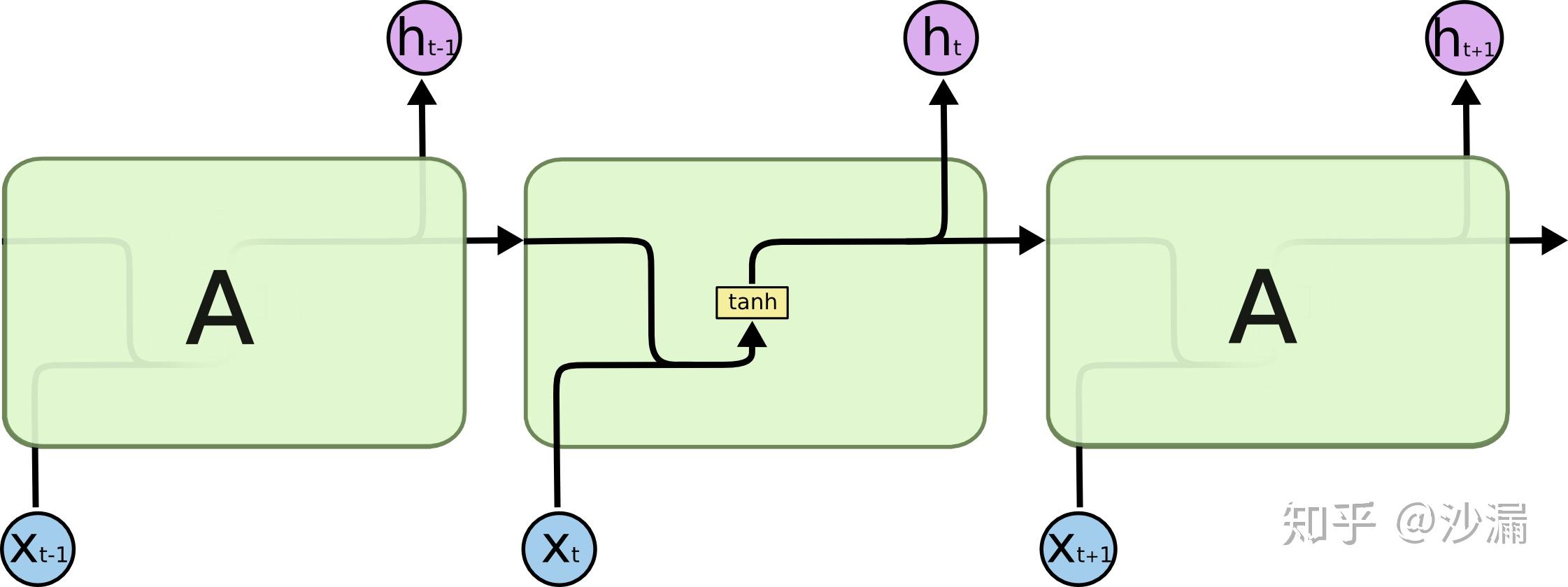
而LSTM在此基础上将这个结构改进了,不再是单一的神经网络层,而是4个,并且以一种特殊的方式进行交互。
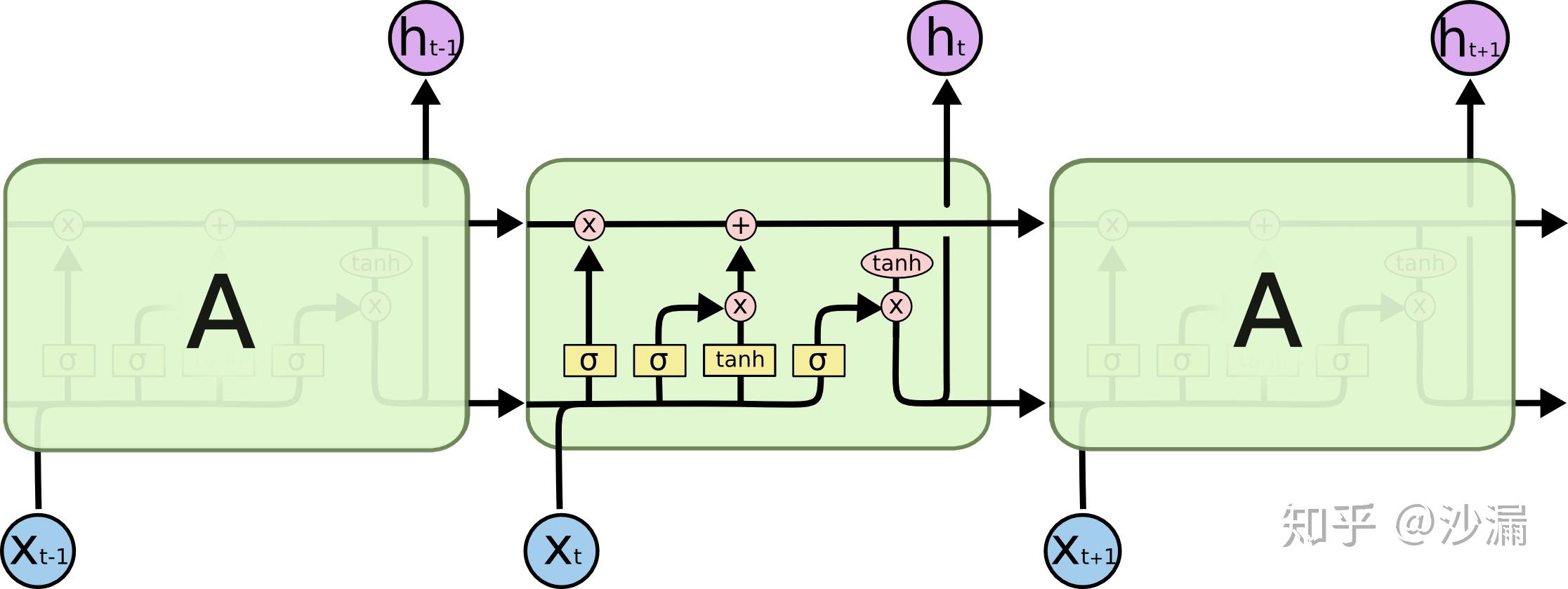
粗看起来,这个结构有点复杂,不过不用担心,接下来我们会慢慢解释。在解释这个神经网络层时我们先来认识一些基本的模块表示方法。图中的模块分为以下几种:

- 黄色方块:表示一个神经网络层(Neural Network Layer);
- 粉色圆圈:表示按位操作或逐点操作(pointwise operation),例如向量加和、向量乘积等;
- 单箭头:表示信号传递(向量传递);
- 合流箭头:表示两个信号的连接(向量拼接);
- 分流箭头:表示信号被复制后传递到2个不同的地方。
下面我们将分别介绍这些模块如何在LSTM中作用。
3.2 LSTM的基本思想
LSTM的关键是细胞状态(直译:cell state),表示为 C_t ,用来保存当前LSTM的状态信息并传递到下一时刻的LSTM中,也就是RNN中那根“自循环”的箭头。当前的LSTM接收来自上一个时刻的细胞状态 C_{t-1} ,并与当前LSTM接收的信号输入 x_t 共同作用产生当前LSTM的细胞状态 C_t ,具体的作用方式下面将详细介绍。
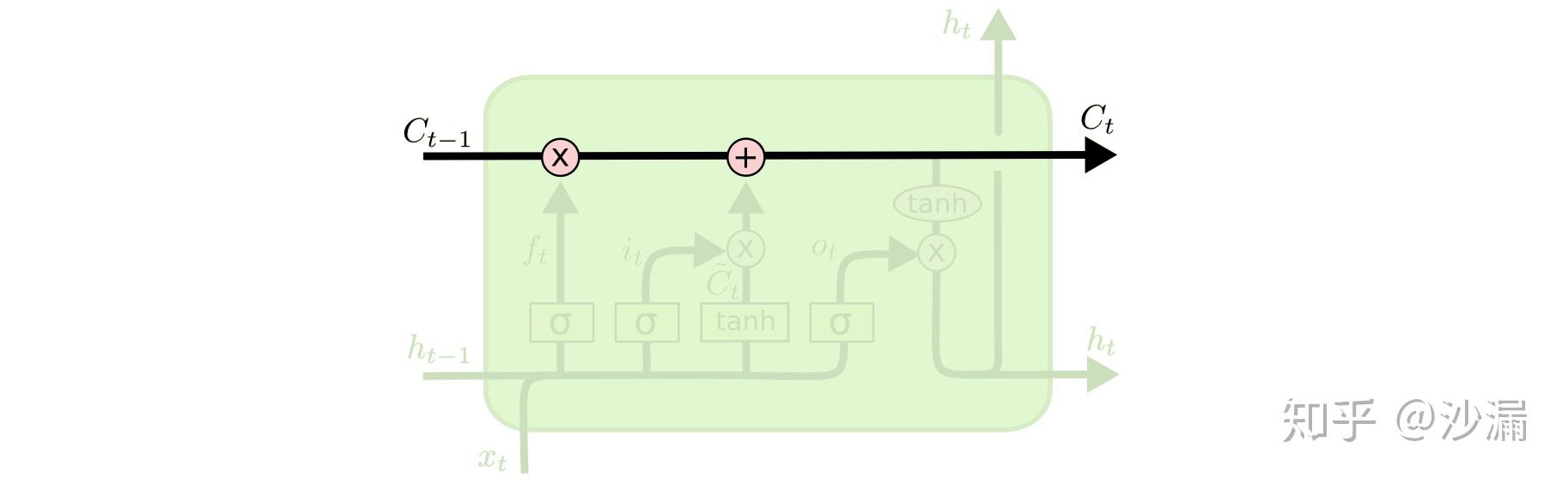
在LSTM中,采用专门设计的“门”来引入或者去除细胞状态 C_t 中的信息。门是一种让信息选择性通过的方法。有的门跟信号处理中的滤波器有点类似,允许信号部分通过或者通过时被门加工了;有的门也跟数字电路中的逻辑门类似,允许信号通过或者不通过。这里所采用的门包含一个 sigmoid 神经网络层和一个按位的乘法操作,如下图所示:
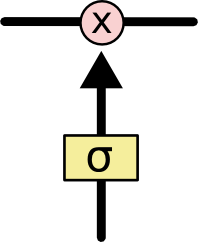
其中黄色方块表示 sigmoid 神经网络层,粉色圆圈表示按位乘法操作。 sigmoid 神经网络层可以将输入信号转换为 0 到 1 之间的数值,用来描述有多少量的输入信号可以通过。 0 表示“不允许任何量通过”, 1 表示“允许所有量通过”。 sigmoid 神经网络层起到类似下图的 sigmoid 函数所示的作用:
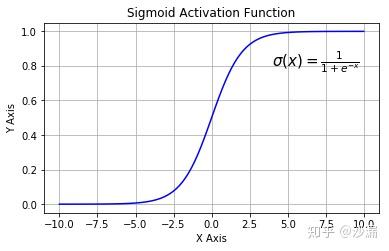
其中,横轴表示输入信号,纵轴表示经过sigmoid函数以后的输出信号。
LSTM主要包括三个不同的门结构:遗忘门、记忆门和输出门。这三个门用来控制LSTM的信息保留和传递,最终反映到细胞状态 C_t 和输出信号 h_t 。如下图所示:
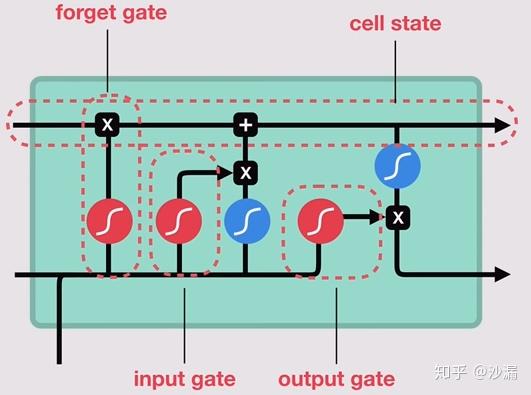
图中标示了LSTM中各个门的构成情况和相互之间的关系,其中:
- 遗忘门由一个 sigmoid 神经网络层和一个按位乘操作构成;
- 记忆门由输入门(input gate)与tanh神经网络层和一个按位乘操作构成;
- 输出门(output gate)与 tanh 函数(注意:这里不是 tanh 神经网络层)以及按位乘操作共同作用将细胞状态和输入信号传递到输出端。
3.3 遗忘门
顾名思义,遗忘门的作用就是用来“忘记”信息的。在LSTM的使用过程中,有一些信息不是必要的,因此遗忘门的作用就是用来选择这些信息并“忘记”它们。遗忘门决定了细胞状态 C_{t-1} 中的哪些信息将被遗忘。那么遗忘门的工作原理是什么呢?看下面这张图。
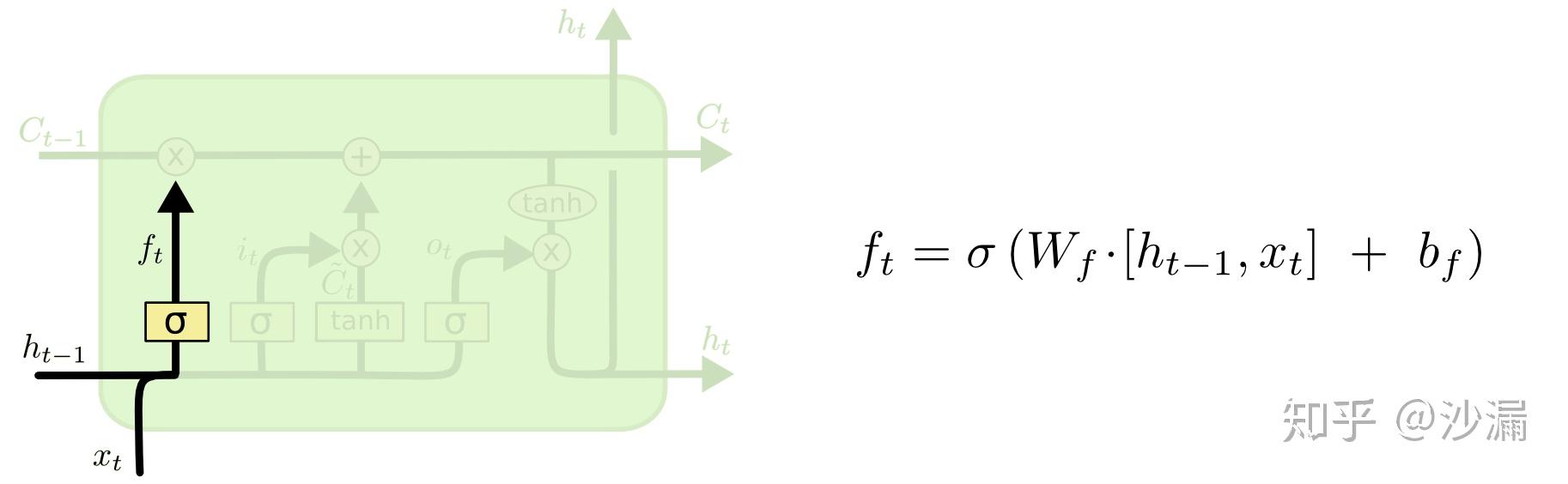
左边高亮的结构就是遗忘门了,包含一个 sigmoid 神经网络层(黄色方框,神经网络参数为 W_f, b_f ),接收 t 时刻的输入信号 x_t 和 t-1 时刻LSTM的上一个输出信号 h_{t-1} ,这两个信号进行拼接以后共同输入到 sigmoid 神经网络层中,然后输出信号 f_t , f_t 是一个 0 到 1 之间的数值,并与 C_{t-1} 相乘来决定 C_{t-1} 中的哪些信息将被保留,哪些信息将被舍弃。可能看到这里有的初学者还是不知道具体是什么意思,我们用一个简单的例子来说明。
假设 C_{t-1} = [0.5, 0.6, 0.4] , h_{t-1}=[0.3, 0.8, 0.69] , x_t=[0.2,1.3,0.7] , 那么遗忘门的输入信号就是 h_{t-1} 和 x_t 的组合,即 [h_{t-1}, x_t] = [0.3, 0.8, 0.69, 0.2, 1.3, 0.7] , 然后通过 sigmoid 神经网络层输出每一个元素都处于 0 到 1 之间的向量 f_t=[0.5, 0.1, 0.8] ,注意,此时 f_t 是一个与 c_{t-1} 维数相同的向量,此处为3维。如果看到这里还没有看懂的读者,可能会有这样的疑问:输入信号明明是6维的向量,为什么 f_t 就变成了3维呢?这里可能是将 sigmoid 神经网络层当成了 sigmoid 激活函数了,两者不是一个东西,初学者在这里很容易混淆。下文所提及的 sigmoid 神经网络层和 tanh 神经网络层而是类似的道理,他们并不是简单的 sigmoid 激活函数和 tanh 激活函数,在学习时要注意区分。
3.4 记忆门
记忆门的作用与遗忘门相反,它将决定新输入的信息 x_t 和 h_{t-1} 中哪些信息将被保留。
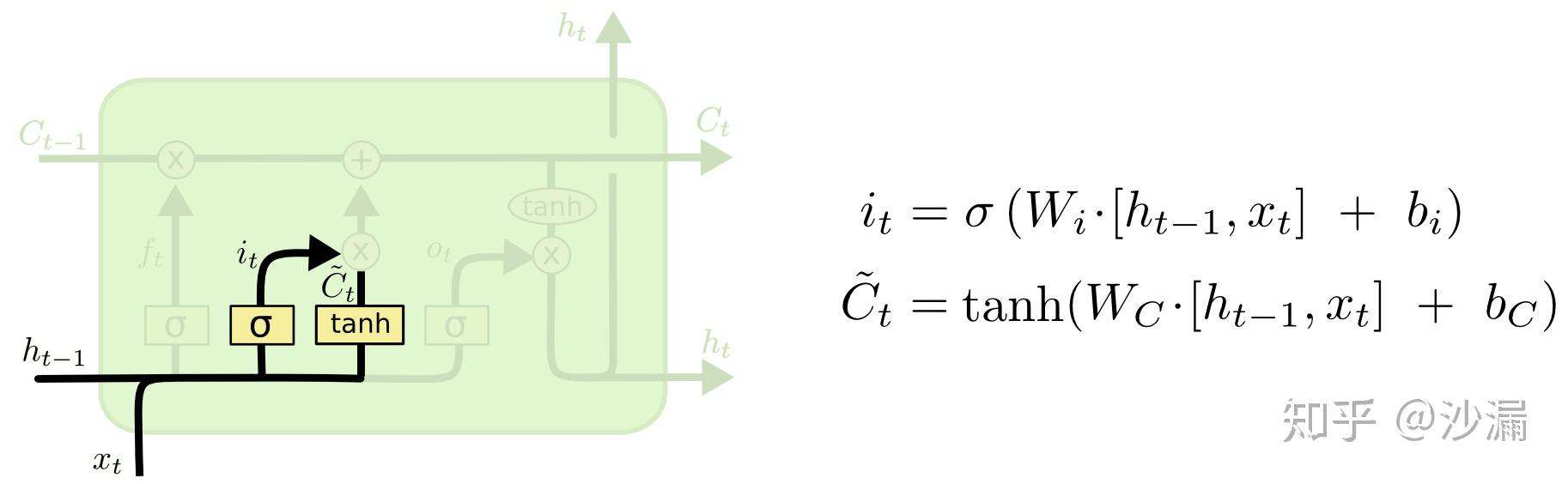
如图所示,记忆门包含2个部分。第一个是包含 sigmoid 神经网络层(输入门,神经网络网络参数为 W_i,b_i )和一个 tanh 神经网络层(神经网络参数为 W_c,b_c )。
- sigmoid 神经网络层的作用很明显,跟遗忘门一样,它接收 x_t 和 h_{t-1} 作为输入,然后输出一个 0 到 1 之间的数值 i_t 来决定哪些信息需要被更新;
- Tanh神经网络层的作用是将输入的 x_t 和 h_{t-1} 整合,然后通过一个 tanh 神经网络层来创建一个新的状态候选向量 \widetilde{C}_t , \widetilde{C}_t 的值范围在 -1 到 1 之间。
记忆门的输出由上述两个神经网络层的输出决定, i_t 与 \widetilde{C}_t 相乘来选择哪些信息将被新加入到 t 时刻的细胞状态 C_t 中。
3.5 更新细胞状态
有了遗忘门和记忆门,我们就可以更新细胞状态 C_t 了。
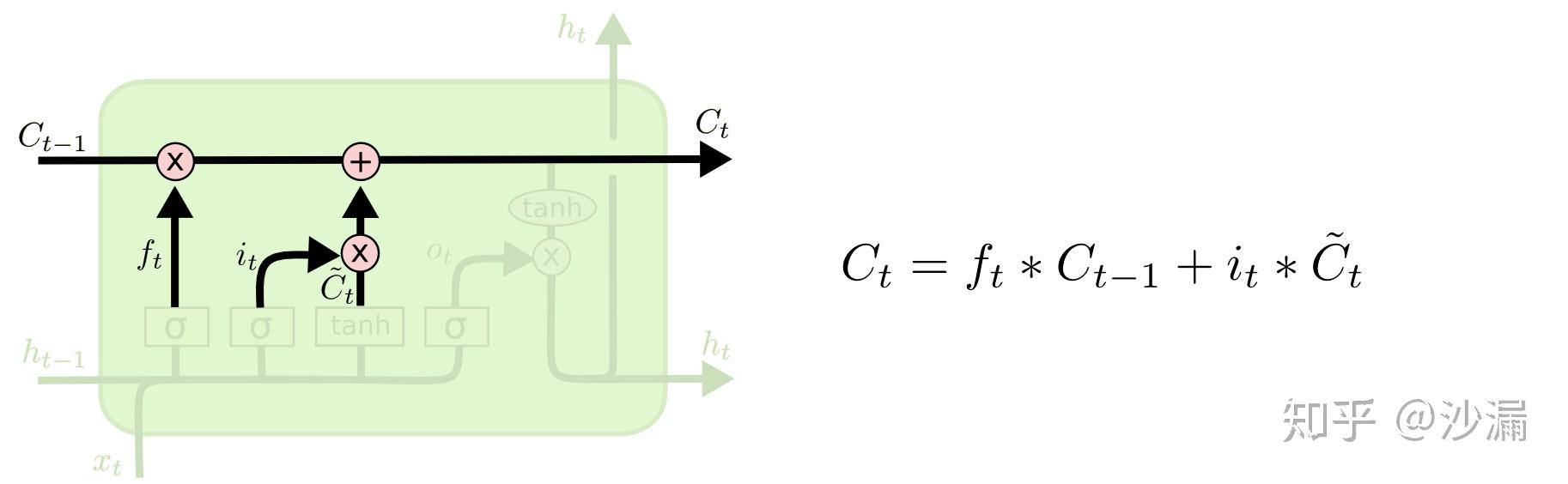
这里将遗忘门的输出 f_t 与上一时刻的细胞状态 C_{t-1} 相乘来选择遗忘和保留一些信息,将记忆门的输出与从遗忘门选择后的信息加和得到新的细胞状态 C_t 。这就表示 t 时刻的细胞状态 C_t 已经包含了此时需要丢弃的 t-1 时刻传递的信息和 t 时刻从输入信号获取的需要新加入的信息 i_t \cdot \widetilde{C}_t 。 C_t 将继续传递到 t+1 时刻的LSTM网络中,作为新的细胞状态传递下去。
3.6 输出门
前面已经讲了LSTM如何来更新细胞状态 C_t , 那么在 t 时刻我们输入信号 x_t 以后,对应的输出信号该如何计算呢?
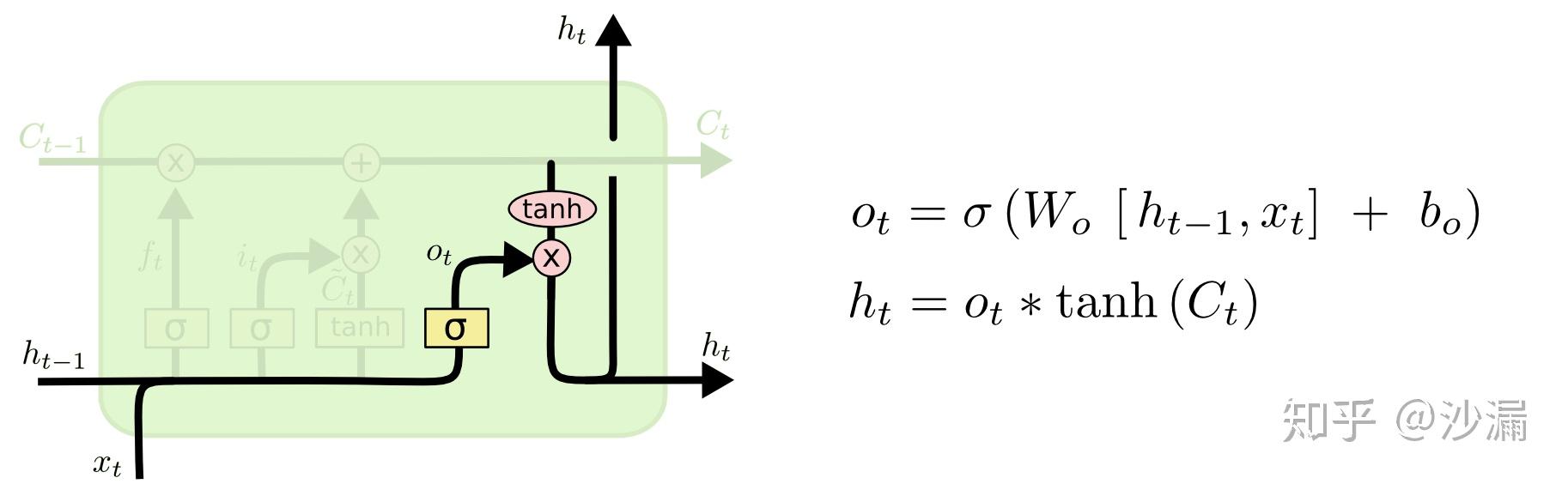
如上面左图所示,输出门就是将 t-1 时刻传递过来并经过了前面遗忘门与记忆门选择后的细胞状态 C_{t-1} , 与 t-1 时刻的输出信号 h_{t-1} 和 t 时刻的输入信号 x_t 整合到一起作为当前时刻的输出信号。整合的过程如上图所示, x_t 和 h_{t-1} 经过一个 sigmoid 神经网络层(神经网络参数为 W_o,b_o )输出一个 0 到 1 之间的数值 o_t 。 C_t 经过一个 tanh 函数(注意:这里不是 tanh 神经网络层)到一个在 -1 到 1 之间的数值,并与 o_t 相乘得到输出信号 h_t ,同时 h_t 也作为下一个时刻的输入信号传递到下一阶段。
其中, tanh 函数是激活函数的一种,函数图像为:
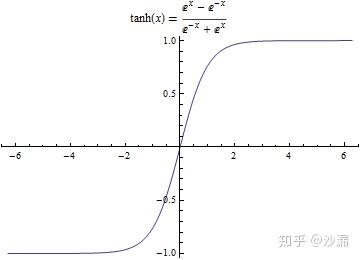
至此,基本的LSTM网络模型就介绍完了。如果对LSTM模型还没有理解到的,可以看一下 这个视频 ,作者是一个外国小哥,英文讲解的,有动图,方便理解。
3.7 LSTM的一些变体
前面已经介绍了基本的LSTM网络模型,而实际应用时,我们常常会采用LSTM的一些变体,虽然差异不大,这里不再做详细介绍,有兴趣的读者可以自行了解。
3.7.1 在门上增加窥视孔
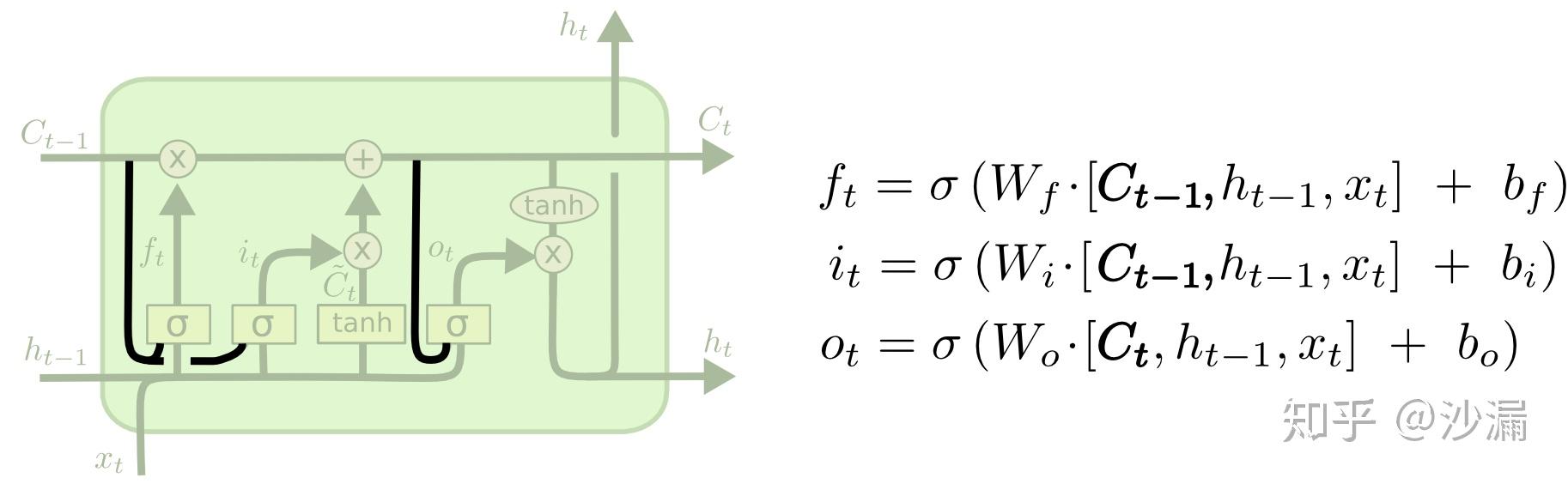
这是2000年Gers和Schemidhuber教授提出的一种LSTM变体。图中,在传统的LSTM结构基础上,每个门(遗忘门、记忆门和输出门)增加了一个“窥视孔”(Peephole),有的学者在使用时也选择只对部分门加入窥视孔。
3.7.2 整合遗忘门和输入门
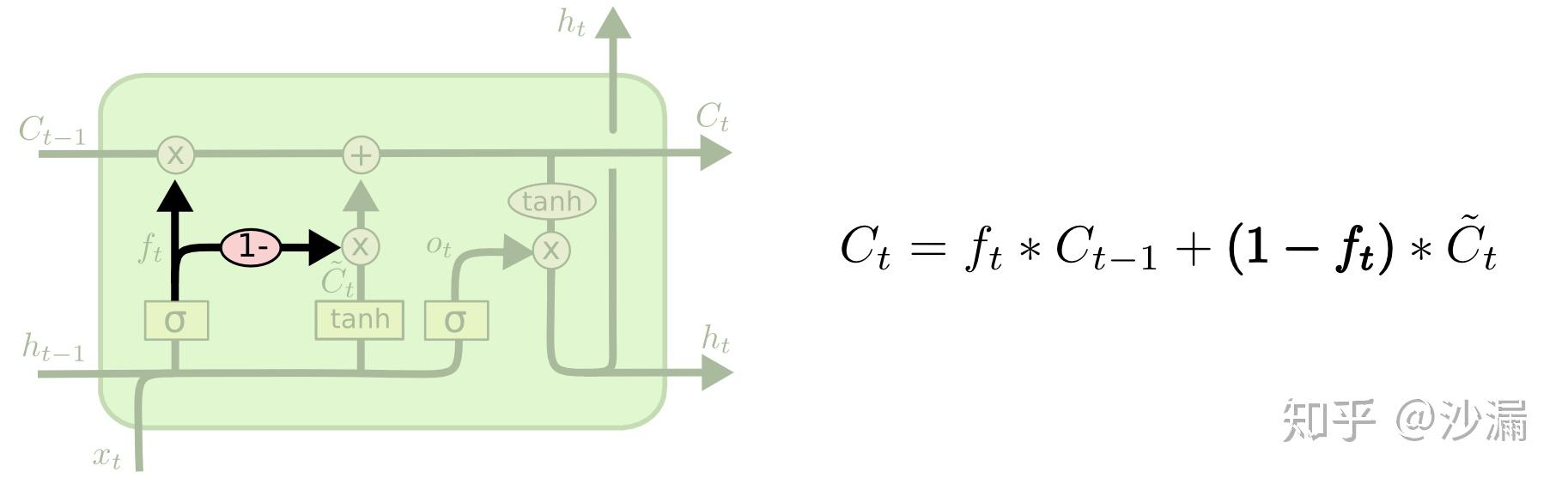
与传统的LSTM不同的是,这个变体不需要分开来确定要被遗忘和记住的信息,采用一个结构搞定。在遗忘门的输出信号值( 0 到 1 之间)上,用 1 减去该数值来作为记忆门的状态选择,表示只更新需要被遗忘的那些信息的状态。
3.7.3 GRU
改进比较大的一个LSTM变体叫Gated Recurrent Unit (GRU),目前应用较多。结构图如下
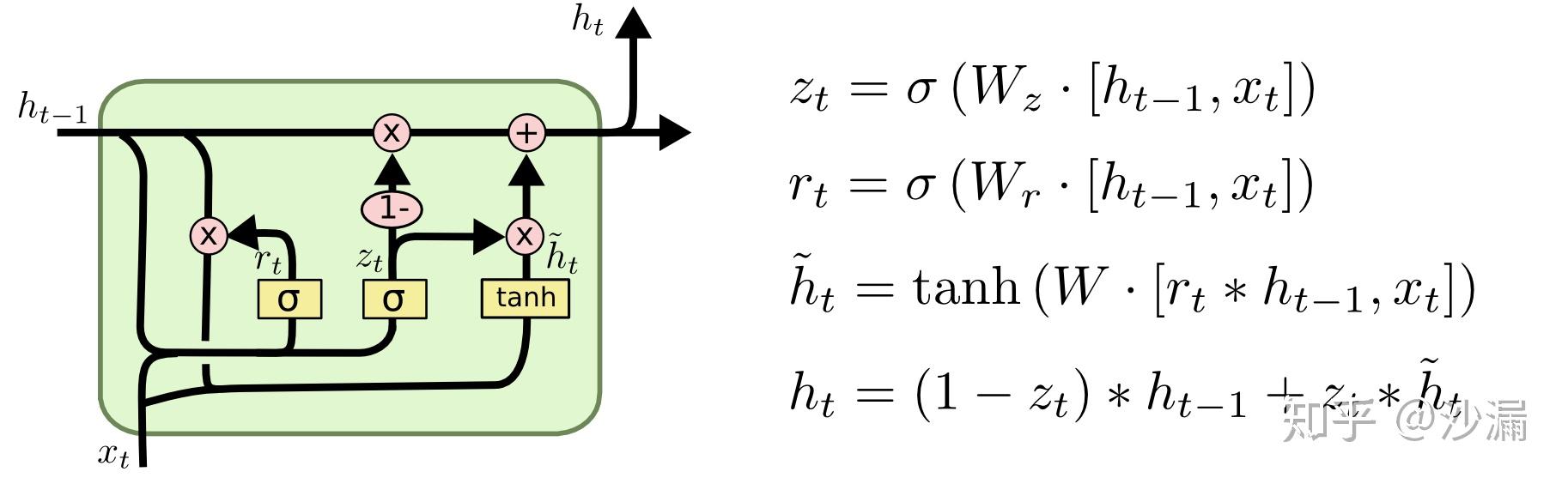
GRU主要包含2个门:重置门和更新门。GRU混合了细胞状态 C_t 和隐藏状态 h_{t-1} 为一个新的状态,使用 h_t 来表示。 该模型比传统的标准LSTM模型简单。
4. 基于Pytorch的LSTM代码实现
Pytorch 是Python的一个机器学习包,与Tensorflow类似,Pytorch非常适合用来构建神经网络模型,并且已经提供了一些常用的神经网络模型包,用户可以直接调用。下面我们就用一个简单的小例子来说明如何使用Pytorch来构建LSTM模型。
我们使用正弦函数和余弦函数来构造时间序列,而正余弦函数之间是成导数关系,所以我们可以构造模型来学习正弦函数与余弦函数之间的映射关系,通过输入正弦函数的值来预测对应的余弦函数的值。
正弦函数和余弦函数对应关系图如下图所示:
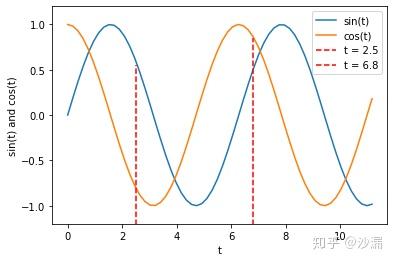
可以看到,每一个函数曲线上,每一个正弦函数的值都对应一个余弦函数值。但其实如果只关心正弦函数的值本身而不考虑当前值所在的时间,那么正弦函数值和余弦函数值不是一一对应关系。例如,当 t=2.5 和 t=6.8 时, sin(t)=0.5 ,但在这两个不同的时刻, cos(t) 的值却不一样,也就是说如果不考虑时间,同一个正弦函数值可能对应了不同的几个余弦函数值。对于传统的神经网络来说,它仅仅基于当前的输入来预测输出,对于这种同一个输入可能对应多个输出的情况不再适用。
我们取正弦函数的值作为LSTM的输入,来预测余弦函数的值。基于Pytorch来构建LSTM模型,采用1个输入神经元,1个输出神经元,16个隐藏神经元作为LSTM网络的构成参数,平均绝对误差(LMSE)作为损失误差,使用Adam优化算法来训练LSTM神经网络。基于Anaconda和Python3.6的完整代码如下:
# -*- coding:UTF-8 -*-
import numpy as np
import torch
from torch import nn
import matplotlib.pyplot as plt
# Define LSTM Neural Networks
class LstmRNN(nn.Module):
Parameters:
- input_size: feature size
- hidden_size: number of hidden units
- output_size: number of output
- num_layers: layers of LSTM to stack
def __init__(self, input_size, hidden_size=1, output_size=1, num_layers=1):
super().__init__()
self.lstm = nn.LSTM(input_size, hidden_size, num_layers) # utilize the LSTM model in torch.nn
self.forwardCalculation = nn.Linear(hidden_size, output_size)
def forward(self, _x):
x, _ = self.lstm(_x) # _x is input, size (seq_len, batch, input_size)
s, b, h = x.shape # x is output, size (seq_len, batch, hidden_size)
x = x.view(s*b, h)
x = self.forwardCalculation(x)
x = x.view(s, b, -1)
return x
if __name__ == '__main__':
# create database
data_len = 200
t = np.linspace(0, 12*np.pi, data_len)
sin_t = np.sin(t)
cos_t = np.cos(t)
dataset = np.zeros((data_len, 2))
dataset[:,0] = sin_t
dataset[:,1] = cos_t
dataset = dataset.astype('float32')
# plot part of the original dataset
plt.figure()
plt.plot(t[0:60], dataset[0:60,0], label='sin(t)')
plt.plot(t[0:60], dataset[0:60,1], label = 'cos(t)')
plt.plot([2.5, 2.5], [-1.3, 0.55], 'r--', label='t = 2.5') # t = 2.5
plt.plot([6.8, 6.8], [-1.3, 0.85], 'm--', label='t = 6.8') # t = 6.8
plt.xlabel('t')
plt.ylim(-1.2, 1.2)
plt.ylabel('sin(t) and cos(t)')
plt.legend(loc='upper right')
# choose dataset for training and testing
train_data_ratio = 0.5 # Choose 80% of the data for testing
train_data_len = int(data_len*train_data_ratio)
train_x = dataset[:train_data_len, 0]
train_y = dataset[:train_data_len, 1]
INPUT_FEATURES_NUM = 1
OUTPUT_FEATURES_NUM = 1
t_for_training = t[:train_data_len]
# test_x = train_x
# test_y = train_y
test_x = dataset[train_data_len:, 0]
test_y = dataset[train_data_len:, 1]
t_for_testing = t[train_data_len:]
# ----------------- train -------------------
train_x_tensor = train_x.reshape(-1, 5, INPUT_FEATURES_NUM) # set batch size to 5
train_y_tensor = train_y.reshape(-1, 5, OUTPUT_FEATURES_NUM) # set batch size to 5
# transfer data to pytorch tensor
train_x_tensor = torch.from_numpy(train_x_tensor)
train_y_tensor = torch.from_numpy(train_y_tensor)
# test_x_tensor = torch.from_numpy(test_x)
lstm_model = LstmRNN(INPUT_FEATURES_NUM, 16, output_size=OUTPUT_FEATURES_NUM, num_layers=1) # 16 hidden units
print('LSTM model:', lstm_model)
print('model.parameters:', lstm_model.parameters)
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(lstm_model.parameters(), lr=1e-2)
max_epochs = 10000
for epoch in range(max_epochs):
output = lstm_model(train_x_tensor)
loss = loss_function(output, train_y_tensor)
loss.backward()
optimizer.step()
optimizer.zero_grad()
if loss.item() < 1e-4:
print('Epoch [{}/{}], Loss: {:.5f}'.format(epoch+1, max_epochs, loss.item()))
print("The loss value is reached")
break
elif (epoch+1) % 100 == 0:
print('Epoch: [{}/{}], Loss:{:.5f}'.format(epoch+1, max_epochs, loss.item()))
# prediction on training dataset
predictive_y_for_training = lstm_model(train_x_tensor)
predictive_y_for_training = predictive_y_for_training.view(-1, OUTPUT_FEATURES_NUM).data.numpy()
# torch.save(lstm_model.state_dict(), 'model_params.pkl') # save model parameters to files
# ----------------- test -------------------
# lstm_model.load_state_dict(torch.load('model_params.pkl')) # load model parameters from files
lstm_model = lstm_model.eval() # switch to testing model
# prediction on test dataset
test_x_tensor = test_x.reshape(-1, 5, INPUT_FEATURES_NUM) # set batch size to 5, the same value with the training set
test_x_tensor = torch.from_numpy(test_x_tensor)
predictive_y_for_testing = lstm_model(test_x_tensor)
predictive_y_for_testing = predictive_y_for_testing.view(-1, OUTPUT_FEATURES_NUM).data.numpy()
# ----------------- plot -------------------
plt.figure()
plt.plot(t_for_training, train_x, 'g', label='sin_trn')
plt.plot(t_for_training, train_y, 'b', label='ref_cos_trn')
plt.plot(t_for_training, predictive_y_for_training, 'y--', label='pre_cos_trn')
plt.plot(t_for_testing, test_x, 'c', label='sin_tst')
plt.plot(t_for_testing, test_y, 'k', label='ref_cos_tst')
plt.plot(t_for_testing, predictive_y_for_testing, 'm--', label='pre_cos_tst')
plt.plot([t[train_data_len], t[train_data_len]], [-1.2, 4.0], 'r--', label='separation line') # separation line
plt.xlabel('t')
plt.ylabel('sin(t) and cos(t)')
plt.xlim(t[0], t[-1])
plt.ylim(-1.2, 4)

