Dowhy,一个强大的Python库,做金融量化领域的可以尝试下!

引言
在数据科学和机器学习领域, 因果推断是一个重要的课题 。旨在从数据中识别变量之间的因果关系,比如说:“如果我做了某件事,会发生什么?”这类问题,而非仅是描述“某件事与其他事情有关联”。
Dowhy
作为一个用于因果推断的Python工具包,提供了一种简单而强大的方法来进行因果推断分析。
介绍
Dowhy
是一个由微软发布的端到端的用于
因果推断(Causal Inference)
的 Python 库。

旨在简化从数据中识别因果关系的过程。
Dowhy
提供了一整套统一标准的API,支持从建模到识别,再到因果效应估计和验证的整个工作流程。
主要特点:
- • 基于一定经验假设的基础上,将问题转化为因果图,验证假设。
- • 提供因果推断的接口,整合了两种因果框架。
- • DoWhy支持对后门、前门和工具的平均因果效应的估计,自动验证结果的准确性、鲁棒性较高。
Dowhy 的整个因果推断过程可以划分为四大步骤:
-
•
「建模」(model):利用假设(先验知识)对因果推断问题建模。 -
•
「识别」(identify):在假设(模型)下识别因果效应的表达式(因果估计量)。 -
•
「估计」(estimate):使用统计方法对表达式进行估计。 -
•
「反驳」(refute):使用各种鲁棒性检查来验证估计的正确性。

安装及API使用
接下来,为大家介绍下Dowhy库的安装和基本用法。
包括如何加载数据、定义因果模型、进行因果推断分析等。
安装
Dowhy的安装同其他Python三方库一样,直接使用pip命令安装即可。
pip install dowhy如果存在依赖,需额外安装pygraphviz库
API使用步骤:
1、导入所需的库, 并加载数据(这里以加载csv文件为例)
# 导入所需的库
import pandas as pd
import dowhy
from dowhy import CausalModel
# 加载数据
data = dowhy.datasets.linear_dataset(
beta=10, # 因果效应值
num_common_causes=5, # 混杂因子,用w表示,作用于干预变量和结果变量
num_instruments=2, # 工具变量,用 Z 表示,作用于干预变量(间接影响结果)
num_samples=10000, # 样本数量
treatment_is_binary=True) # 干预为二元变量,用 v 表示
df = data["df"] # DoWhy 使用 pandas 的 dataframe 来载入数据
print(df.head(5))输出数据:
Z0 Z1 W0 W1 W2 W3 W4 v0 y
0 0.0 0.478130 0.313025 0.274645 1.794765 -1.551661 1.250724 True 17.033979
1 0.0 0.546833 -0.197845 -2.404349 1.120160 -1.011344 0.812087 True 3.074740
2 0.0 0.874135 1.047078 -0.056460 0.440413 -0.067349 0.970203 True 15.530070
3 0.0 0.913483 0.934282 -1.180582 0.498135 -1.079074 -1.659924 True 5.046809
4 0.0 0.366969 -0.364818 0.630643 -0.330043 0.572139 -0.433893 True 11.004590
2、执行因果推断,建模,生成因果关系图
model=CausalModel(
data = df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=data["gml_graph"]
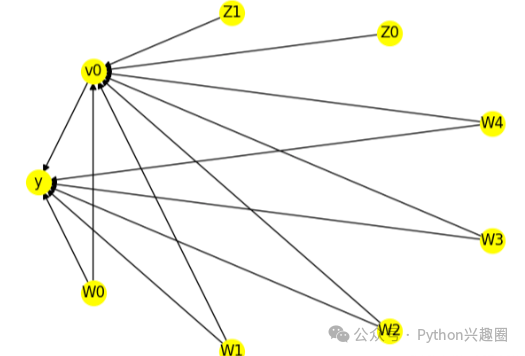
model.view_model() # 对构建的因果图可视化
from IPython.display import Image, display
display(Image(filename="causal_model.png"))利用这张图来识别因果效应(从因果估计量到概率表达式)并进行估计。
3、识别和估计因果关系
识别
可以脱离于数据,仅根据图进行识别,其给出的结果是一个用于计算的「表达式」。
identified_estimand = model.identify_effect()
print(identified_estimand)输出结果:
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
─────(E[y|W1,W0,W4,W2,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W0,W4,W2,W3,U) = P(y|v0,W1,W0,W4,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
⎡ -1⎤
⎢ d ⎛ d ⎞ ⎥
E⎢─────────(y)⋅⎜─────────([v₀])⎟ ⎥
⎣d[Z₁ Z₀] ⎝d[Z₁ Z₀] ⎠ ⎦
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0}→{v0}, then ¬({Z1,Z0}→y)
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!估计
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_stratification")
print(estimate)输出结果:
*** Causal Estimate ***
## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE
### Estimand : 1
Estimand name: backdoor
Estimand expression:
─────(E[y|W1,W0,W4,W2,W3])
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W0,W4,W2,W3,U) = P(y|v0,W1,W0,W4,W2,W3)