4.4 吸收边界

梁昊

物理学话题下的优秀答主

在数值求解薛定谔方程时，人们往往会面临这样一个情况：所关心的动力学仅仅局限在空间中一个狭小的区域中，但是波函数却会有一部分不停地向外传播和扩散。我们不希望为了跑出去的那一点点波函数而使用一个非常大的求解域（更可怕的是，这个求解域是随着求解总时长增长的），但取一个小的求解域，如何取边界条件便成了个恼人的事情。不论是自由边界条件（导数值为零）还是固定边界条件（函数值为零）亦或是混合，都会造成波函数在边界上的反射，从而反过来影响所关心区域中的动力学。为了解决这个问题，三十年余来人们发展了各种技术，一般统称为吸收边界。这里我们仅讨论由拉伸变换出发的 复标度延拓(exterior complex scaling) 技术。

我们回忆一下Balslev-Combes定理的最初版本：束缚态本征值不变，依同一形式变化；连续态本征值带虚部，本身渐进行为不变。如果我们关心的动力学完全由束缚态描述，那直接将哈密顿量做一个复旋转就够了，那些会跑出去的连续态都会带上一个指数衰减因子，跑到边界上时已经不剩多少了。此外，跑得越快的连续态( k 越大)，衰减得越快( \exp(-\frac{k^2}{2}\sin(2\beta) t) )，可以保证一个都不放过。

当然，连续态往往也会贡献动力学，尤其是在一些中间过程。这时我们就要想到之前举的那个泛函极值问题的视角了——积分轨道是可以随便取的！如果我们依下图的形式来选取变换

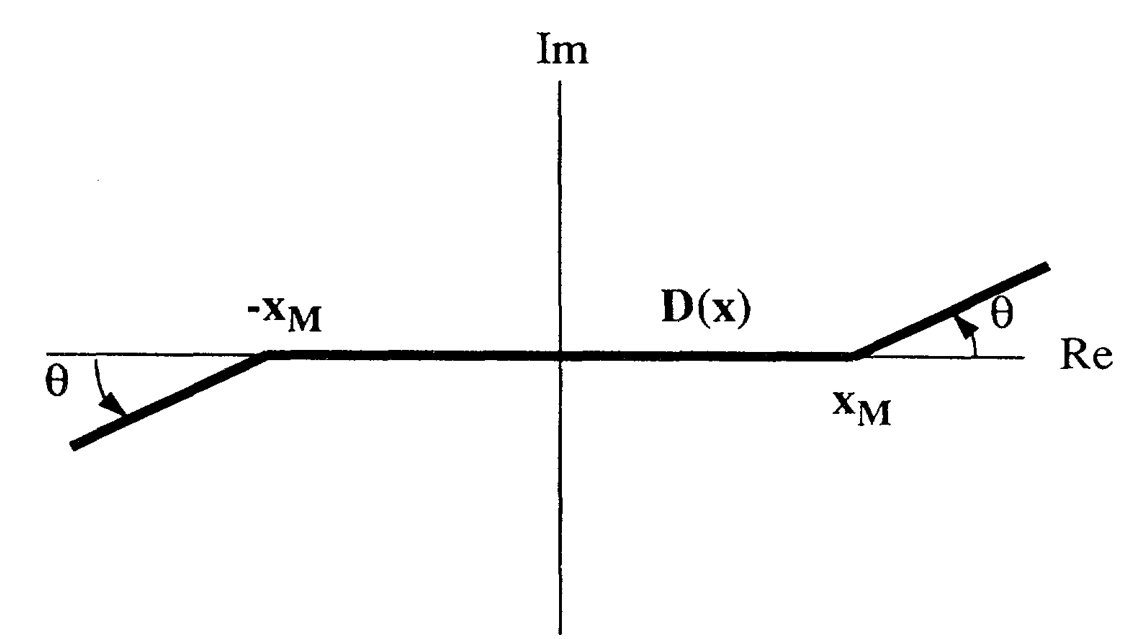
由于改变轨道对函数的影响是局域的，从而在中间实轴上那段区域，任何动力学都和没改变时相同。而在两侧，复旋转能够衰减掉跑出去的连续态波函数，从而实现一个理想的吸收。

此时我们仍需要辨析一下概念：

1. 有明确动量的连续态是分布在整个空间中的

2. 当我们谈论空间某处的连续态时，谈论的是一个波包，对应有一个动量分布

3. 之前讨论能谱问题时，将波函数限定在 L^2 之中，但是在数值离散化之后，会出现那些本征值为实数的非 L^2 的成分

4. 这些成分并不可怕，因为从中心往外传播的波包始终满足 k\cdot x>0 ，对应衰减过程。而在恰当的初态下不存在发散的从外向内传播的波包

5. 它们在内部表现为平稳传播，在复旋转后的网格上呈现空间上 \exp(-kx\sin\beta ) 的衰减，算上波包群速度 \mathrm dE/\mathrm dk_p = k/\cos\beta 传播后，表现为波包在时间上以 \exp(-\frac{k_p^2t}{2}\sin2\beta ) 的衰减，即两类连续态的行为实际上是一样的。

---

光说不练假把式，我们来看个算例

考虑零势场下的一维问题。由于坐标变换后的问题是积分格式，故我们采取基函数的办法来导出离散后的方程。即

\[ \psi(x,t) \approx \sum_n c_n(t)f_n(x), \]

取基函数为分段线性插值函数 f_n(x) :

\[ f_n(x) = \begin{cases} \frac{x-x_{n-1}}{x_n-x_{n-1}},&x_{n-1}<x<x_n,\\ \frac{x_{n+1}-x}{x_{n+1}-x_n},&x_n<x<x_{n+1},\\ 0,&\text{else}. \end{cases} \]

由于现在是在复坐标上研究问题，从而坐标格点也在复路径上分划，具体而言

complexco = 
  Join[Array[zmin + Exp[I \[Beta]] # &, 
    Round[absorb/dx], {-absorb, -dx}], 
   Array[# &, Round[(zmax - zmin)/dx] + 1, {zmin, zmax}], 
   Array[zmax + Exp[I \[Beta]] # &, Round[absorb/dx], {dx, absorb}]];

其中的参数取值为

absorb = 15;
zmin = -15.;
zmax = 15.;
dx = 0.1;
\[Beta] = 45 Degree;

通过计算积分可以得到交叠矩阵 S 和动能矩阵 T :

\[ S_{ij} = \int f_i(z)f_j(z)\,\mathrm dz,\quad T_{ij}=\frac{1}{2}\int f_i'(z)f_j'(z)\,\mathrm dz. \]

即

overlap = (DiagonalMatrix[#[[3 ;;]] - #[[;; -3]]]/3 + 
      DiagonalMatrix[#[[3 ;; -2]] - #[[2 ;; -3]], 1]/6 + 
      DiagonalMatrix[#[[3 ;; -2]] - #[[2 ;; -3]], -1]/6) &@complexco;
kinetic = (DiagonalMatrix[
        1/(#[[2 ;; -2]] - #[[;; -3]]) + 1/(#[[3 ;;]] - #[[2 ;; -2]])]/
       2 + DiagonalMatrix[-1/(#[[3 ;; -2]] - #[[2 ;; -3]]), 1]/2 + 
      DiagonalMatrix[-1/(#[[3 ;; -2]] - #[[2 ;; -3]]), -1]/2) &@
   complexco;

之后，我们可以使用Crank-Nicolson传播子进行含时传播

\[ \bm c(t+\Delta t) = \frac{S-\mathrm i T\Delta t/2}{S+\mathrm iT\Delta t/2}\bm c(t), \]

我们考虑最简单的高斯波包的解，即

\[ \psi(x,t) = \frac{1}{\sqrt{1+2\mathrm i\alpha (t-t_0)}}\exp\left\{-\frac{\alpha}{1+2\mathrm i\alpha(t-t_0)}[x-x_0-p_0(t-t_0)]^2+\mathrm ip_0(t-t_0)\right\}, \]

计算中我们考虑中心动量为零，和有一个明显的非零值两种情况。示例代码如下

dt = 0.01;
total = 4.5;
mop = 10.;
analytic =