[Python] 二维曲线拟合 ( 含有笔记、代码、注释 )


多项式拟合一次函数
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from numpy import polyfit, poly1d
%matplotlib inline
x = np.linspace(-5, 5, 100) # 产生[-5,5]的100个等间隔的数组
y = 4 * x + 1.5 # y是关于x的一次函数
noise_y = y + np.random.randn(y.shape[-1]) * 2.5 # y添加噪声后的函数值。
print(y.shape[-1]) # 100个元素运行结果:
100
p = plt.plot(x, noise_y, 'rx') # 画红色叉叉就是rx,画红色叉叉虚线图就是rx--
p = plt.plot(x, y, 'b:') # 画蓝色点图,"b" 表示蓝色,":"表示点图。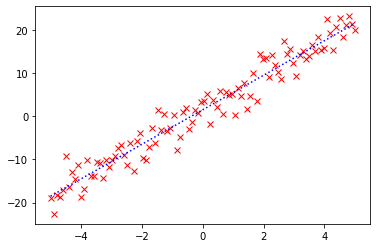
coeff = polyfit(x, noise_y, 1)
print(coeff)运行结果:
[4.00355516 1.55927961]
p = plt.plot(x, noise_y, 'rx')
p = plt.plot(x, coeff[0] * x + coeff[1], 'k-') # 画黑色实线图,"k" 表示实线,"-"表示实线。
p = plt.plot(x, y, 'b--') # 这里可看出拟合出一阶函数与原函数重合了,课通过注释该语句看出。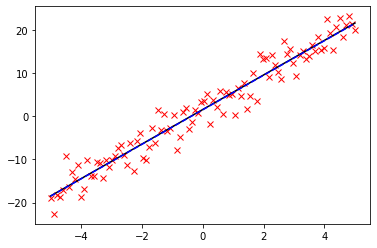
# 还可以用 poly1d 生成一个以传入的 coeff 为参数的多项式函数:
f = poly1d(coeff)
p = plt.plot(x, noise_y, 'rx') # 绘制红色叉叉散点图
p = plt.plot(x, f(x)) # 带入x点,画出f函数。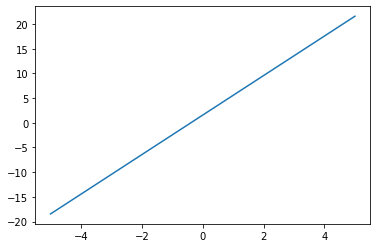
多项式拟合正弦函数
x = np.linspace(-np.pi,np.pi,100)
y = np.sin(x)
# 用一阶到九阶多项式拟合,类似泰勒展开:
y1 = poly1d(polyfit(x,y,1))
y3 = poly1d(polyfit(x,y,3))
y5 = poly1d(polyfit(x,y,5))
y7 = poly1d(polyfit(x,y,
7))
y9 = poly1d(polyfit(x,y,9))
x = np.linspace(-3 * np.pi,3 * np.pi,100)
p = plt.plot(x, np.sin(x), 'k') # 黑色为原始的图形,
p = plt.plot(x, y1(x))
p = plt.plot(x, y3(x))
p = plt.plot(x, y5(x))
p = plt.plot(x, y7(x))
p = plt.plot(x, y9(x)) # 可以看到,随着多项式拟合的阶数的增加,曲线与拟合数据的吻合程度在逐渐增大。
a = plt.axis([-3 * np.pi, 3 * np.pi, -1.25, 1.25])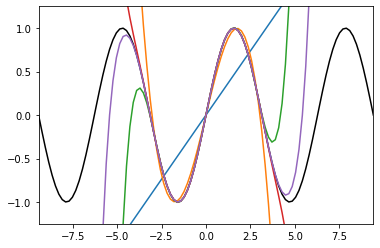
最小二乘拟合
from scipy.linalg import lstsq
x = np.linspace(0,5,100)
y = 0.5 * x + np.random.randn(x.shape[-1]) * 0.35
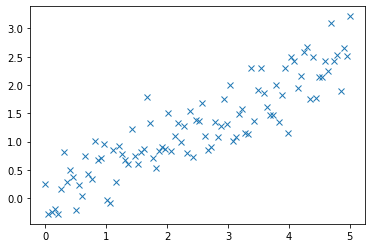
plt.plot(x,y,'x') # 产生含有一定线性关系的散点图,含有噪音。运行结果:
[<matplotlib.lines.Line2D at 0x251c6b60970>]
X = np.hstack((x[:,np.newaxis], np.ones((x.shape[-1],1)))) # 这里将x扩展成X了,这里N=2。
X[1:5]运行结果:
array([[0.05050505, 1. ],
[0.1010101 , 1. ],
[0.15151515, 1. ],
[0.2020202 , 1. ]])
C, resid, rank, s = lstsq(X, y)
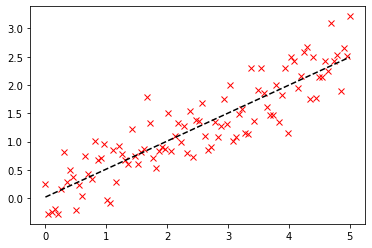
p = plt.plot(x, y, 'rx')
p = plt.plot(x, C[0] * x + C[1], 'k--')
print("sum squared residual = {:.3f}".format(resid)) # 平方和残差
print("rank of the X matrix = {}".format(rank)) # 秩
print("singular values of X = {}".format(s)) # X的奇异值运行结果:
sum squared residual = 12.986
rank of the X matrix = 2
singular values of X = [30.23732043 4.82146667]
线性回归拟合
from scipy.stats import linregress
slope, intercept, r_value, p_value, stderr = linregress(x, y)
slope, intercept运行结果:
(0.5028457518511993, 0.024071946424871093)
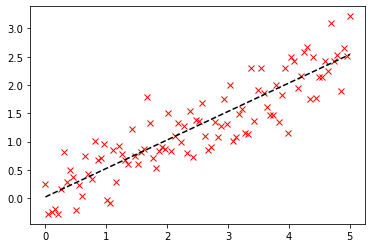
p = plt.plot(x, y, 'rx')
p = plt.plot(x, slope * x + intercept, 'k--') # 由图可以看出两者(线性回归、最小二乘)求解的结果是一致的,但是出发的角度是不同的。
print("R-value = {:.3f}".format(r_value))
print("p-value (probability there is no correlation) = {:.3e}".format(p_value))
print("Root mean squared error of the fit = {:.3f}".format(np.sqrt(stderr)))运行结果:
R-value = 0.912
p-value (probability there is no correlation) = 1.254e-39
Root mean squared error of the fit = 0.151
更高级的拟合
from scipy.optimize import leastsq
def function(x, a , b, f, phi): # 定义非线性函数
"""a function of x with four parameters"""
result = a * np.exp(-b * np.sin(f * x + phi))
return result
x = np.linspace(0, 2 * np.pi, 50)
actual_parameters = [3, 2, 1.25, np.pi / 4] # 实际参数
y = function(x, *actual_parameters)
p = plt.plot(x,y) # 画出实际的x、y函数。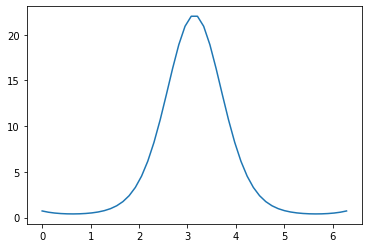
from scipy.stats import norm
y_noisy = y + 0.8 * norm.rvs(size=len(x)) # 加入噪声
p = plt.plot(x, y, 'k-')
p = plt.plot(x, y_noisy, 'rx')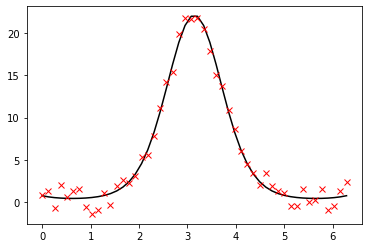
# 定义误差函数,将要优化的参数放在前面:
def f_err(p, y, x):
return y - function(x, *p)
# 将这个函数作为参数传入 leastsq 函数,第二个参数为初始值:
c, ret_val = leastsq(f_err, [1, 1, 1, 1], args=(y_noisy, x))
print(c)
print(ret_val) # ret_val是 1~4 时,表示成功找到最小二乘解:
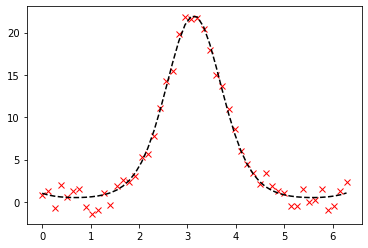
p = plt.plot(x, y_noisy, 'rx')
p = plt.plot(x, function(x, *c), 'k--')运行结果:
[3.32130888 1.89218577 1.28617493 0.68515905]
1
# 更高级的做法:不需要定义误差函数,直接传入function作为参数。
from scipy.optimize import curve_fit