图解卡尔曼滤波器,无需深厚的数学知识也易懂(第四部分:一维卡尔曼滤波器【下】)
一维卡尔曼滤波器的完整模型
现在,我们将使用过程噪音变量更新协方差外推方程。
- 过程噪音(PROCESS NOISE)
现实世界中的系统动态模型具有很多的不确定性。例如,当我们想估计电阻器的阻力时,我们假设电阻器是一个恒定动态系统,即,阻力在两次测量之间没有发生变化。然而,如果环境温度发生变化,那么阻力也会有轻微的改变。当使用雷达追踪弹道导弹时,动态模型的不确定度包活目标加速度的随机变化。对于飞行器,由于可能的飞机尾迹,不确定性要大得多。(飞机尾迹是啥啊???别急,特地给大家找了一个图片,聪明如我啊,哈哈哈)

另一方面,如果我们使用GPS接收器估计估计一个静态物体的位置,由于静态物体不会移动,因此,这个静态物体的动态模型就是0.动态模型的不确定度被称为 过程噪声Process Noise 。在文献中,它还称为工厂噪声plant noise,驱动噪声riving noise,动态噪声dynamics noise,模型噪声model noise和系统噪声system noise。 过程噪声会产生估计误差。(在此特地说明一下,看前面这句话你就会发现,一些英文名词要翻译成中文时,其实是有很多争议的,也就是说,并没有一个“最合适”的词语,甚至不同的行业叫法也不一样,为了不混淆概念,大家配合英文名称一起看,更直观也更容易理解)。
在上一个案例中我们估计建筑物的高度。建筑物的高度是不会改变的,因此,我们并不会将过程噪声考虑在内。
过程噪声方差Process Noise Variance 的字母表示:q
协方差外推方程Covariance Extrapolation Equation 将会包含 过程噪声方差Process Noise Variance 。
恒定动态模型(指的是静态模型)的协方差外推方程是:
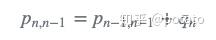
这是更新的一维卡尔曼滤波方程:
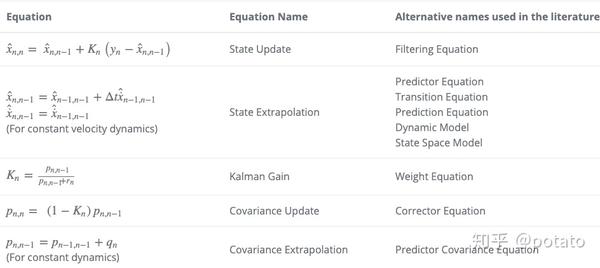
注意1:状态外推方程和协方差外推方程依赖于系统动力学。(每个系统的运动方程方式)
注意2: 上表展示了针对特定情况定制的卡尔曼滤波方程的特殊形式。方程的一般形式将在后面的矩阵表示法中给出。现在,我们的目标是理解卡尔曼滤波器的概念。
案例6: 估计罐中液体的温度
我们将估计罐中液体的温度。

我们假设在稳定状态下,液体温度是恒定的。然而,真实液体温度的一些波动是可能存在的。我们可以用以下方程描述系统动力学:
x_{n}=T+w_{n}
在此方程中:
T表示恒定温度。
w_{n} 是方差q的随机过程噪声。
- 数值案例
— 假设真实温度为50摄氏度。
— 我们认为我们有一个精确的模型,因此我们将过程噪声方差(q)设置为0.0001。
— 测量误差(标准差)为0.1摄氏度。
— 每5秒测量一次。
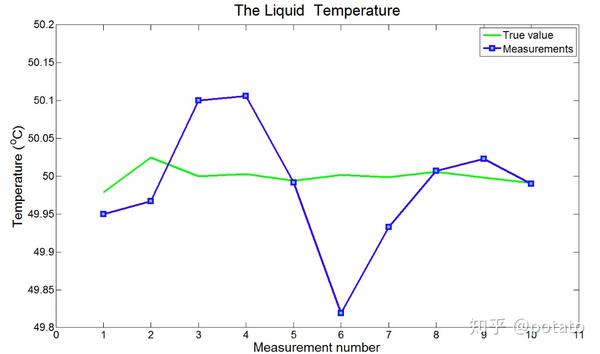
— 液体实际温度为:49.979℃, 50.025℃, 50℃, 50.003℃, 49.994℃, 50.002℃, 49.999℃, 50.006℃, 49.998℃, 49.991℃.
— 测量数据:49.95℃, 49.967℃, 50.1℃, 50.106℃, 49.992℃, 49.819℃, 49.933℃, 50.007℃, 50.023℃, 49.99℃.
下图比较了真实温度与测量温度:
- 第0此迭代:
在第一次迭代之前,我们必须初始化卡尔曼滤波器并预测下一个状态(即第一个状态)。
- 初始化
我们不知道罐里液体的温度是多少,我们初始猜测是10摄氏度。
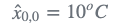
我们的初始猜测非常不准确。我们设置初始估计误差 \sigma=100 。初始 估计不确定度Estimate Uncertainty 是误差方差 \sigma^{2} 。
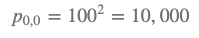
方差非常大。如果我们用一个更有意义的值初始化,我们会更快的得到卡尔曼滤波器收敛。
- 预测
现在,我们将基于初始化值预测下一个状态。
由于我们的模型是恒定动态的,因此预测估计等于当前估计:
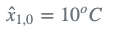
外推估计不确定度(方差):
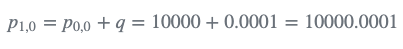
2. 第一次迭代:
- step 1 - 测量
1)测量值是:
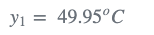
2)由于测量误差为0.1(σ),方差( \sigma^{2} )为0.01,因此测量不确定度为:
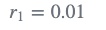
- step 2 - 更新
1)计算卡尔曼增益Kalman Gain:
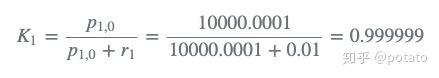
卡尔曼增益Kalman Gain趋近于1,即我们的估计误差远大于测量误差。因此当策略权重趋近于1时,估计权重几乎可以忽略不计。
2)估计当前状态:
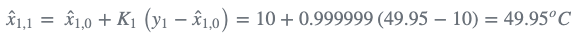
3)更新当前估计不确定度:

- step 3 - 预测
由于使用系统的动态模型是恒定的,即液体温度不变,那么:
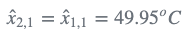
外推估计不确定度(方差)是:

3. 第二次迭代
- step 1 - 测量
1)测量值:
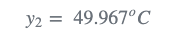
2) 由于测量误差为0.1(σ),方差( \sigma^{2} )为0.01,因此测量不确定度为:
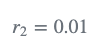
- step 2-更新
1)计算卡尔曼增益Kalman Gain:
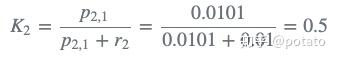
卡尔曼增益为0.5,即估计权重和测量权重相等。
2)估计当前状态:

3)更新当前估计不确定度:
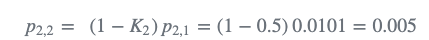
- step 3-预测
由于使用系统的动态模型是恒定的,即液体温度不变,那么:
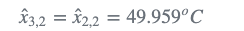
外推估计不确定度(方差)是:

4. 第3-10次迭代:
下表总结了下一次迭代的计算:

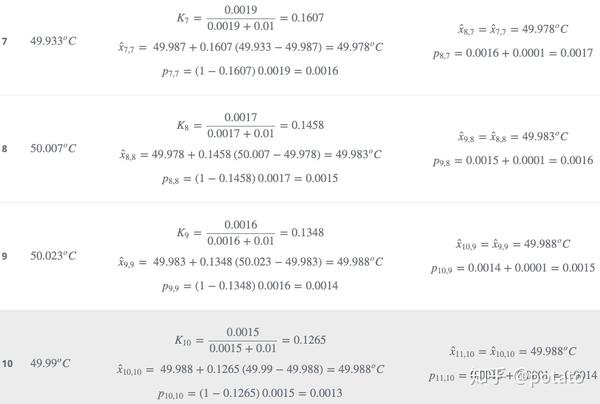
下表比较了真实值、测量值及估计值。
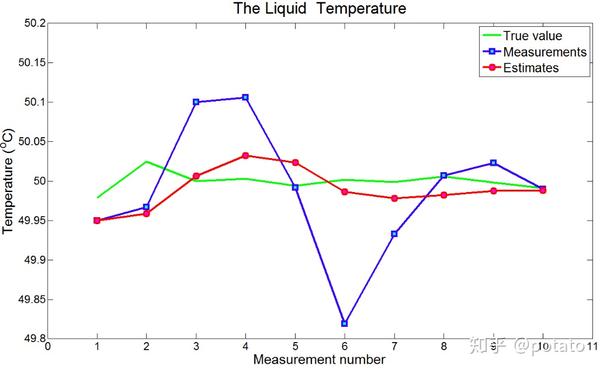
正如你看到的,估计值向真实值收敛。
下图展示了估计不确定度:
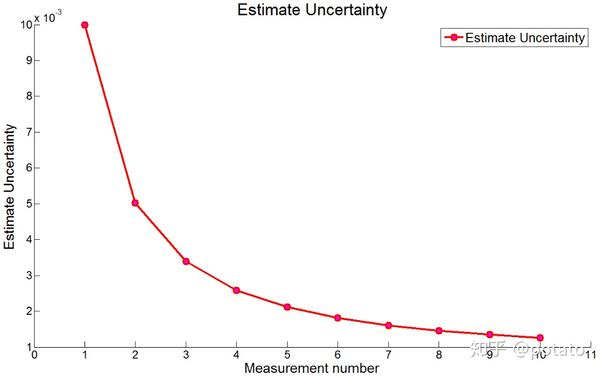
估计不确定度快速下降。10次测量后估计不确定度 \sigma^{2}=0.0013 ,即,估计误差标准差 \sigma=\sqrt{0.0023}=0.036 ℃(注意区分估计不确定度与估计误差)
所以我们可以说液体温度的估计值是: 49.998\pm0.036 ℃
下图展示了卡尔曼增益Kalman Gain:
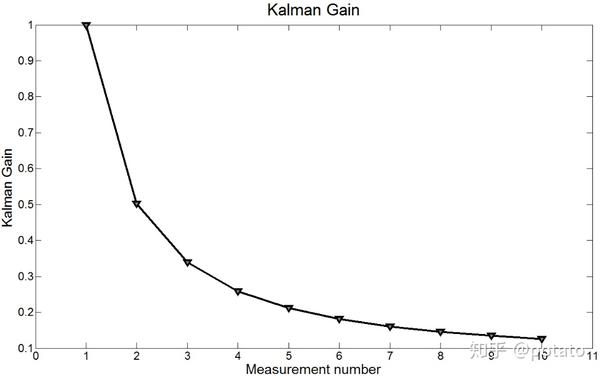
如你所及,卡尔曼增益Kalman Gain快速下降,使得测量权重越来越小。
5. 案例总结
在这个案例中我们使用一维卡尔曼滤波器测量液体温度。尽管系统动力模型伴随随机过程噪声,卡尔曼滤波器依然可以提供一个良好的估计。
案例7:估计正在加热的液体温度
如上一个案例一样,我们将估计罐中的液体温度。这个系统动力模型system dynamics不是恒定的,液体以0.1℃/S的速率加热。
卡尔曼滤波器的参数与上一个案例的参数相似:
- 我们认为我们有一个精确的模型,因此我们将过程噪声方差(q)设置为0.0001。
- 测量误差(标准差)为0.1℃.
- 每5s进行一次测量。
- 系统动力模型是恒定的。
注意,尽管真实的系统模型不是恒定的(液体温度持续上升),我们认为这个系统就是恒定的(温度不会发生改变)。
- 在测量点的真实温度是:50.479℃, 51.025℃, 51.5℃, 52.003℃, 52.494℃, 53.002℃, 53.499℃, 54.006℃, 54.498℃, and 54.991℃.
- 测量数据:50.45℃, 50.967℃, 51.6℃, 52.106℃, 52.492℃, 52.819℃, 53.433℃, 54.007℃, 54.523℃, and 54.99℃。
下图比较了液体真实温度与测量温度:
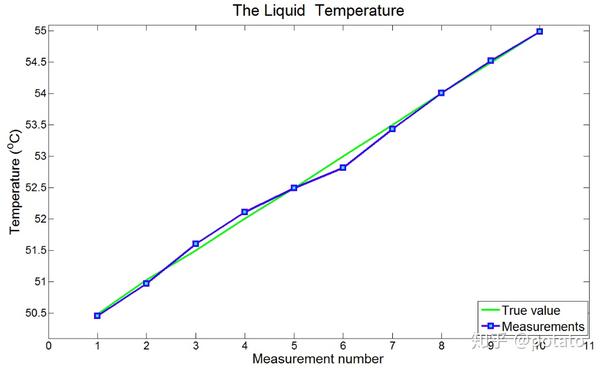
- 第0次迭代
第0次迭代与之前的例子相似。
在第一次迭代之前,我们必须初始化卡尔曼滤波器并预测下一个状态(即第一个状态)。
- 初始化
我们不知道罐里液体的温度是多少,我们初始猜测是10摄氏度。
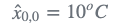
我们的初始猜测非常不准确。我们设置初始估计误差 \sigma=100 。初始 估计不确定度Estimate Uncertainty 是误差方差 \sigma^{2} 。
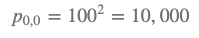
方差非常大。如果我们用一个更有意义的值初始化,我们会更快的得到卡尔曼滤波器收敛。
- 预测
现在,我们将基于初始化值预测下一个状态。
由于我们的模型是恒定动态的,因此预测估计等于当前估计:
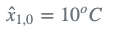
外推估计不确定度(方差):
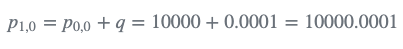
2. 第1-10次迭代:


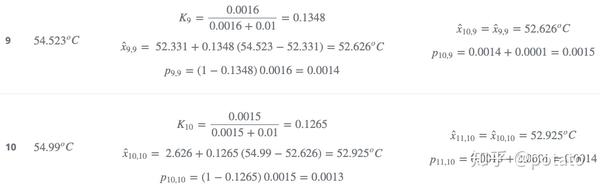
下图比较了真实值、测量值及估计值:
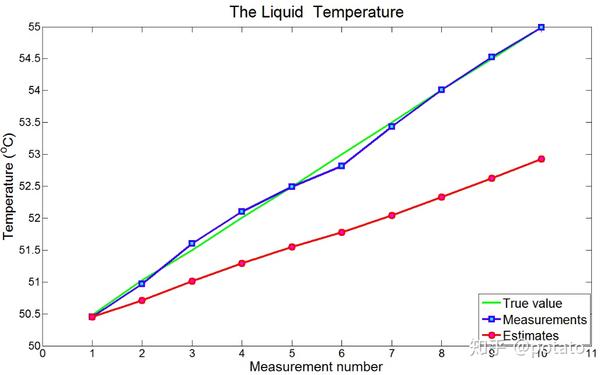
如你所见,卡尔曼增益并没有提供值得信赖的估计值。在卡尔曼增益中存在 滞后误差lag error 。我们在案例3中遇到过滞后误差,在那个案例中我们使用假设飞行器是匀速飞行的α−β滤波器估计加速飞行器的位置。我们在案例4中解决了滞后误差的问题,在案例4中,我们使用假设加速运动的α−β−γ滤波器替换了假设匀速飞行的α−β滤波器。
在我们的卡尔曼滤波器案例中引起滞后误差的原因有两个:
- 系统动力模型与实际不符。
- 过程模型的可靠性。我们选择了非常低的过程噪声(q=0.0001),而实际温度波动要大得多。
注意:滞后误差应为常数,因此估计曲线应与真值曲线具有相同的斜率。上面的图只显示了前10个测量值,不足以收敛。下图显示了前100个具有恒定滞后误差的测量。
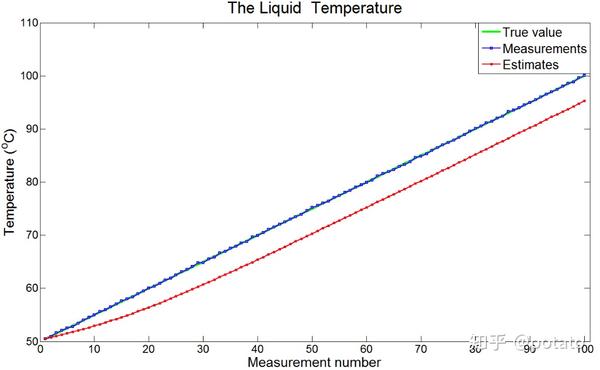
有两种可能的方法解决滞后误差问题:
- 如果我们知道液体温度是线性变化的,我们可以定义一个将温度可能的线性变化考虑进去的新模型。在案例4中我们就是这么做的。这个一个好方法。然而,如果温度改变不能被建模,这个方法也不足以提升卡尔曼增益的性能。
- 另一方面,由于我们的模型并没有被很好的定义,因此我们可以同感增加过程噪声(q)来提高模型可靠度。细节见下一个案例。
3. 案例总结
在这个案例中,我们使用了一个恒定系统动力模型的一维卡尔曼滤波器来测量温度变化的液体温度。我们在卡尔曼滤波器估计中观察了滞后误差。这个滞后误差是由错误的系统动力模型与错误的过程模型导致的。
滞后误差可以通过合理的定义系统动力模型与过程模型得到解决。
案例8:估计正在加热的液体温度
除了一些细微的变化以外,这个案例与上一个案例很相似。由于我们的过程不确定度并没有被很好的定义,因此,我们将过程不确定度q由0.0001增加到0.15。
- 第0次迭代
在第一次迭代之前,我们必须初始化卡尔曼滤波器并预测下一个状态(即第一个状态)。
- 初始化
第0次迭代与上一个案例相似。
我们不知道罐里液体的温度是多少,我们初始猜测是10摄氏度。
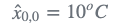
我们的初始猜测非常不准确。我们设置初始估计误差 \sigma=100 。初始 估计不确定度Estimate Uncertainty 是误差方差 \sigma^{2} 。
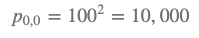
方差非常大。如果我们用一个更有意义的值初始化,我们会更快的得使卡尔曼滤波器收敛。
- 预测
现在,我们将基于初始化值预测下一个状态。
由于我们的模型是恒定动态的,因此预测估计等于当前估计:
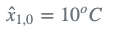
外推估计不确定度(方差):
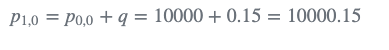
2. 第1-10次迭代



下图比较了真实值、测量值及估计值:
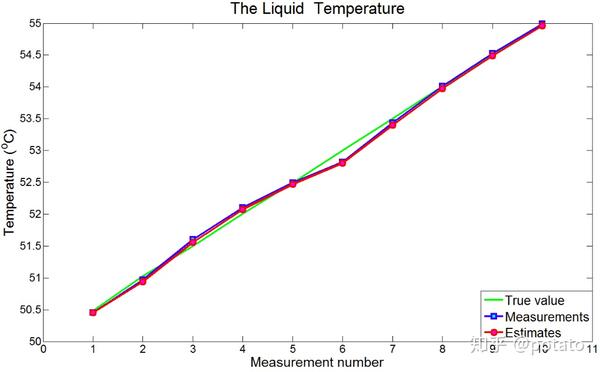
如你所见,估计值与测量值基本一致,无滞后误差。
下图展示了卡尔曼增益:
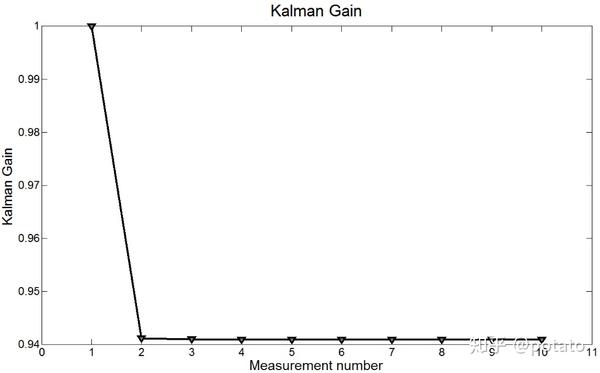
由于过程不确定度较高,测量权重远高于估计权重,因此卡尔曼增益很高,收敛到0.94。
3. 案例总结:
我们通过设置高的过程不确定度解决了滞后误差问题。然后,由于我们的模型依然没有更好的被定义,我们的估计误差几乎与测量误差一样高,卡尔曼滤波器是失效的。
最好的卡尔曼滤波器实现应该是模型与现实情况高度一致,几乎不会存在过程噪声。然而,精确的模型并不总有,例如,飞行员可以决定执行一个突然的动作(如大转弯、紧急刹车等等)从而改变预测的飞行轨迹,在这种情况下,过程噪音将会增加。
一些话:
关于卡尔曼滤波器的第一大部分就此结束,接下来将开始第二大部分,多维空间中的卡尔曼滤波器multidimensional Kalman Filter (Kalman Filter in matrix notation)。

