深蓝学院多传感器融合课程第一期课程1

2 年前 · 来自专栏其他文章

杨熙

胡同里的技术土著。善良，专注

深蓝学院多传感器融合课程第一期课程1 学习记录

代码放在github: yandld/shenlan_multi_sensor_fusion

第一课内容：

ICP 算法推导
NDT算法推导
LOAM/LEGO LOAM代码分析

ICP算法推导

主要参考:Least-Squares Rigid Motion Using SVD .自己理解，翻译得来。主要是推导最基础的点点ICP的原理：

摘要：这篇笔记总结了激光SLAM中如何计算最基础的点点ICP的数学推导过程。

问题的定义

定义 \mathcal{P}=\left\{\mathbf{p}_{1}, \mathbf{p}_{2}, \ldots, \mathbf{p}_{n}\right\} 和 \mathcal{Q}=\left\{\mathrm{q}_{1}, \mathrm{q}_{2}, \ldots, \mathrm{q}_{n}\right\} ， \mathcal{P} 和 \mathcal{Q} 是两个二维空间或者三维空间中的点集合(激光SLAM数据)。我们要寻找一个"最可能的"位姿变换 R , t 使得代价函数最小，数学表达如下：

其中 w_{i}>0 是每一个数据点的权重。

求解平移向量t

先假设 R 已经被求出来了，记 F(\mathbf{t})=\sum_{i=1}^{n} w_{i}\left\|\left(R \mathbf{p}_{i}+\mathbf{t}\right)-\mathbf{q}_{i}\right\|^{2} 。我们可以通过 F(t) 对 t 求导的放出求出最优的 t :

轻松可得：

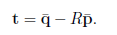
也就是说：最优的 t 实际上就是把 \mathcal{P} 的几何中心(平均值)平移到 \mathcal{Q} 的几何中心上。下面的问题就是求解旋转矩阵 R ，使得 R 满足：

其中 X_{i}, Y{_i} 为两个点集的几何中心：

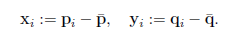
求解旋转矩阵R

展开公式8，得到：

注意到 \mathbf{x}_{i}^{\top} R^{\top} \mathbf{y}_{i} 是一个标量，有： \mathbf{x}_{i}^{\top} R^{\top} \mathbf{y}_{i}=\left(\mathbf{x}_{i}^{\top} R^{\top} \mathbf{y}_{i}\right)^{\top}=\mathbf{y}_{i}^{\top} R \mathbf{x}_{i}

于是得到：

于是乎：这里来了最精彩的部分：

最小话和最大化转换一下：

最终得到：

其中

W=\operatorname{diag}\left(w_{1}, \ldots, w_{n}\right) 是一个 n \times n 对角矩阵，包含了 i 上每一个点的权重 w_{i}
Y 是一个 d \times n (d是维数，比如2或者3)的矩阵，每一个激光点 y_{i} 作为一列
X 是一个 d \times n (d是维数，比如2或者3)的矩阵，每一个激光点 x_{i} 作为一列

问题现在转换为：寻找一个旋转矩阵 R 是的最大化 \operatorname{tr}\left(W Y^{\top} R X\right) 。注意到矩阵的迹有性质： \operatorname{tr}(A B)=\operatorname{tr}(B A) .所以有：

定义 d \times d 协方差矩阵为 S=X W Y^{\top} ，然后将 S 进行SVD分解： S=U \Sigma V^{\top} ，将SVD分解的结果带入16：

注意到 V,R,U 都是正交矩阵，所以 M=V^{\top} R U 必然也是一个正交矩阵。等价于 M 的每一列相互正交切长度的为1的向量，所以有 \mathrm{m}_{j}^{\top} \mathrm{m}_{j}=1 ，对于 M 中的任意元素 m_{i j} 都有 m_{i j}<1

下面是神奇的部分!!!

那么 \operatorname{tr}(\Sigma M) 的最大值多低怎么求呢？不要忘记 \Sigma 是对角矩阵，所以对于任意非负对角线元素： \sigma_{1}, \sigma_{2}, \ldots, \sigma_{d} \geq 0 有：

如果说当 M 矩阵的每一个对角线元素 m_{ii}=1 的时候， \operatorname{tr}(\Sigma M) 有最大值，但是 M 是一个正交矩阵呀！所以只有当 M 是单位阵的时候才能有 m_{ii}=1 !!!

所以 最终结论 ： R=V U^{\top}

总结

1. 问题的定义：代价函数：

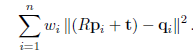
2. 计算两个点集合的几何中心：

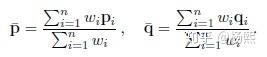
3. 得到中心化的点集(均值平移到0上)：

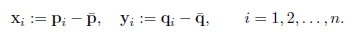
4. 计算两个点集写方差矩阵：

5. SVD分解协方差矩阵，得到R:

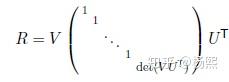
6. 求得平移向量：

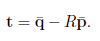
第一课作业

对于搞嵌入式开发的我做这第一个作业有点头疼，ubantu系统，装ROS，速成ROS，配套库安装就折腾了半天，虚拟机还经常死机。。只是把第一题做出来了。。(虚拟机实在是太卡了，这课要继续上下去估计要买电脑了。。)

1. 了解 KITTI 数据集,完成相关依赖库的安装,运行作业代码,提供程序运行成功的截图(参考 PPT 基于数据集实现的 1, 2 项)

第一题，不需要任何编程，环境搭起来，KITTI数据集跑起来就可以了。中间遇到的一些磕磕碰碰没啥说的，都是非算法问题。需要运行命令为：rviz -d display_bag.rviz

2. 在作业代码中,仿照写好的基于 NDT 的匹配,重新建立一个基于 ICP 的里程计(可以
使用 PCL),要求可在配置文件中切换两种方法。之后使用 evo 评估两种算法得到的轨迹
精度(参考 PPT 基于数据集实现的 3, 4 项);

照猫画虎把ICP hpp,cpp 添加上了，并且网上搜了一个ICP IterativeClosestPoint 的demo，照着套上了：

hpp里内容如下：

/*
 * @Description: icp 匹配模块
 * @Author: Ren Qian
 * @Date: 2020-02-08 21:46:57
#ifndef LIDAR_LOCALIZATION_MODELS_REGISTRATION_ICP_REGISTRATION_HPP_
#define LIDAR_LOCALIZATION_MODELS_REGISTRATION_ICP_REGISTRATION_HPP_
#include <pcl/registration/icp.h>
#include "lidar_localization/models/registration/registration_interface.hpp"
namespace lidar_localization {
class ICPRegistration: public RegistrationInterface {
  public:
    ICPRegistration(const YAML::Node& node);
    ICPRegistration(float res, float step_size, float trans_eps, int max_iter);
    bool SetInputTarget(const CloudData::CLOUD_PTR& input_target) override;
    bool ScanMatch(const CloudData::CLOUD_PTR& input_source, 
                   const Eigen::Matrix4f& predict_pose, 
                   CloudData::CLOUD_PTR& result_cloud_ptr,
                   Eigen::Matrix4f& result_pose) override;
  private:
    bool SetRegistrationParam(float res, float step_size, float trans_eps, int max_iter);
  private:
    pcl::IterativeClosestPoint<CloudData::POINT, CloudData::POINT>::Ptr ndt_ptr_;
#endif

cpp里内容如下，参数直接写死了先试试：

/*
 * @Description: NDT 匹配模块
 * @Author: Ren Qian
 * @Date: 2020-02-08 21:46:45
#include "lidar_localization/models/registration/icp_registration.hpp"
#include "glog/logging.h"
namespace lidar_localization {
ICPRegistration::ICPRegistration(const YAML::Node& node)
    :ndt_ptr_(new pcl::IterativeClosestPoint<CloudData::POINT, CloudData::POINT>()) {
    // float res = node["res"].as<float>();
    // float step_size = node["step_size"].as<float>();
    // float trans_eps = node["trans_eps"].as<float>();
    // int max_iter = node["max_iter"].as<int>();
    float res = 1;
    float step_size = 1;
    float trans_eps = 1e-6;
    int max_iter = 50;
    SetRegistrationParam(res, step_size, trans_eps, max_iter);
ICPRegistration::ICPRegistration(float res, float step_size, float trans_eps, int max_iter)
    :ndt_ptr_(new pcl::IterativeClosestPoint<CloudData::POINT, CloudData::POINT>()) {
    SetRegistrationParam(res, step_size, trans_eps, max_iter);
bool ICPRegistration::SetRegistrationParam(float res, float step_size, float trans_eps, int max_iter) {
  //  ndt_ptr_->setResolution(res);
  //  ndt_ptr_->setStepSize(step_size);
    ndt_ptr_->setMaxCorrespondenceDistance(1);
    ndt_ptr_->setEuclideanFitnessEpsilon(1);
    ndt_ptr_->setTransformationEpsilon(1e-4);
    ndt_ptr_->setMaximumIterations(30);
    LOG(INFO) << "NDT 的匹配参数为：" << std::endl
              << "res: " << res << ", "
              << "step_size: " << step_size << ", "
              << "trans_eps: " << trans_eps << ", "
              << "max_iter: " << max_iter 
              << std::endl << std::endl;
    return true;
bool ICPRegistration::SetInputTarget(const CloudData::CLOUD_PTR& input_target) {
    ndt_ptr_->setInputTarget(input_target);
    return true;
bool ICPRegistration::ScanMatch(const CloudData::CLOUD_PTR& input_source, 
                                const Eigen::Matrix4f& predict_pose, 
                                CloudData::CLOUD_PTR& result_cloud_ptr,
                                Eigen::Matrix4f& result_pose) {
    ndt_ptr_->setInputSource(input_source);
    ndt_ptr_->align(*result_cloud_ptr, predict_pose);