03.平均磁链法的证明


引题:在《新概念物理教程——电磁学》中有这样一道题:电流在内柱横截面上均匀分布,从外侧回流,已知内外半径分别是 R_{1}和R_{2} (R_{1}>R_{2}) ,其间介质的磁导率为 \mu 。
欢迎大家对不足之处提出指正。
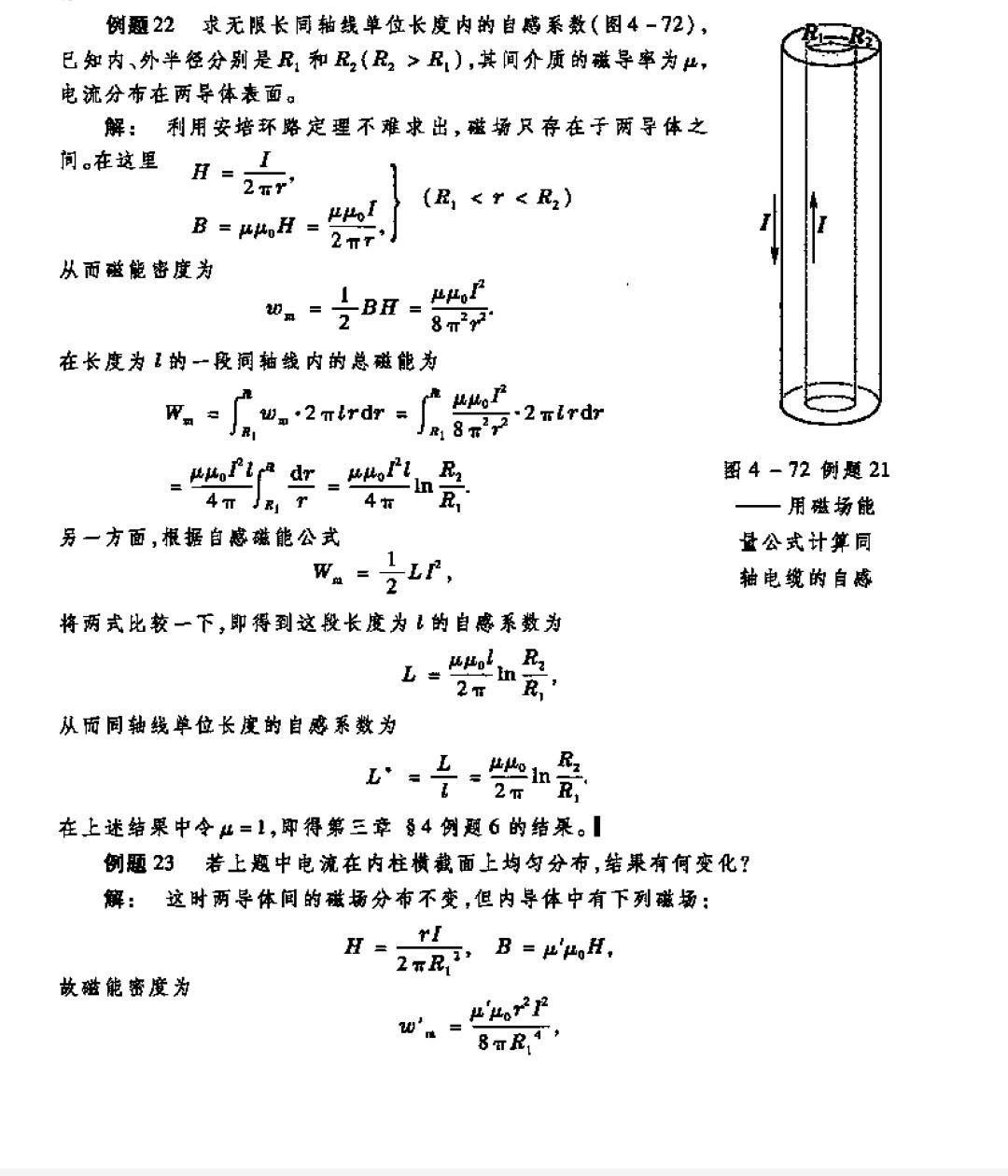

原答案采用了计算单位长度内电感器的能量的方法,代入 E=\frac{1}{2}LI^{2} 得到 L 的值。接着原书在下面介绍了计算有横截面积的导体回路的自感系数的三种方法:分别是磁能法、平均磁链法一和二:
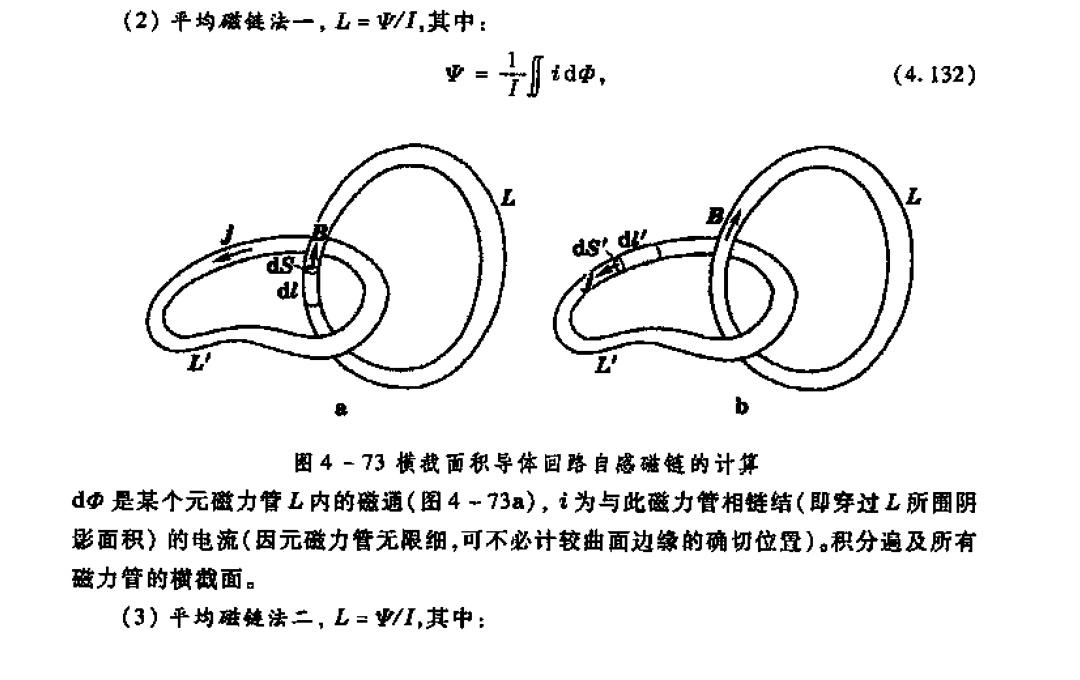

这两个式子赵凯华教授在自己的文章里证明过: 也谈“三维导体”的自感系数 。赵凯华教授给出了很严谨简洁的证明,下面我想分享一下我不太严谨的方法:
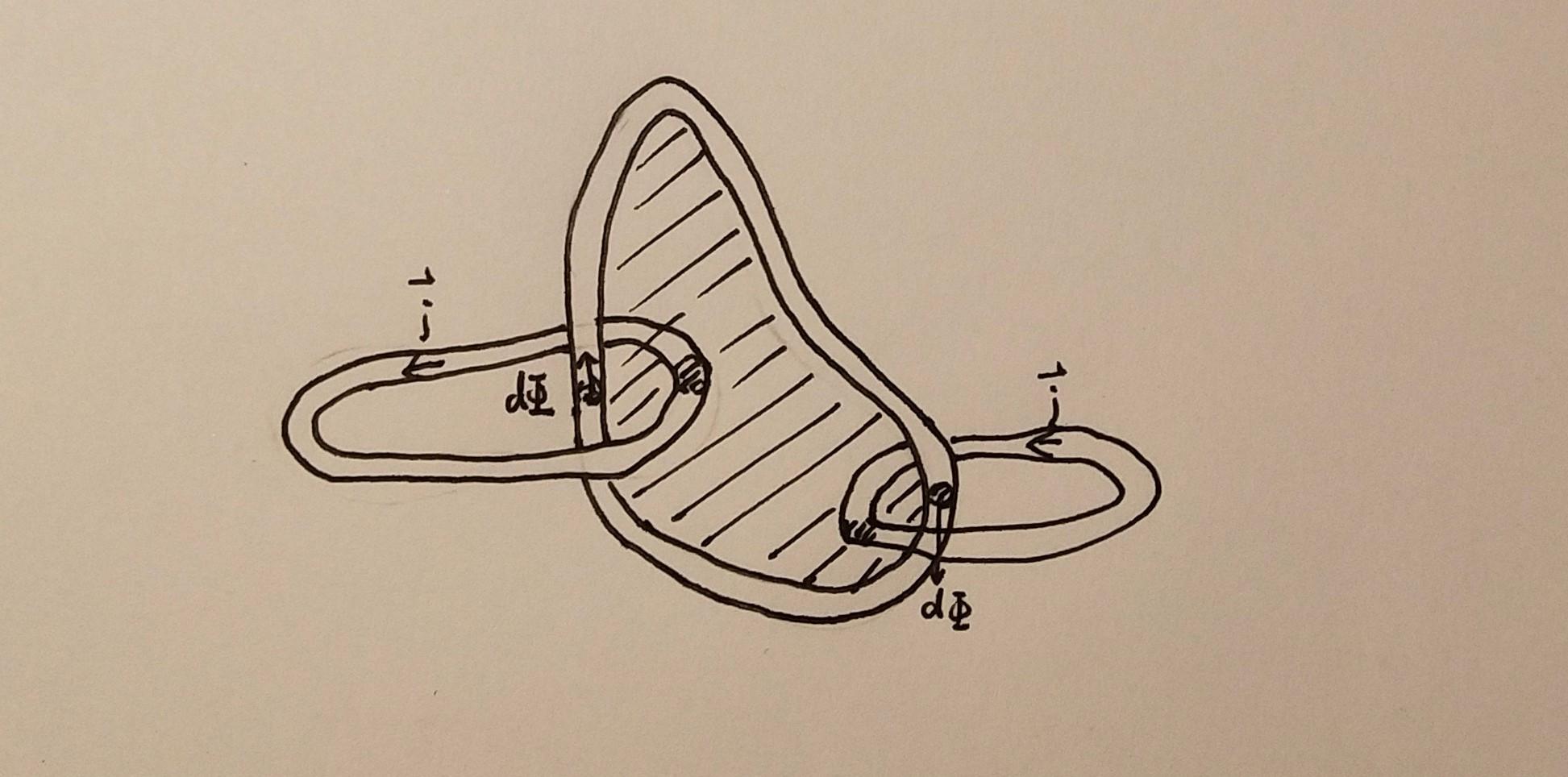
如图所示,在取的磁通量微元管围成的区域内会有电流通过,不妨规定:穿过该区域的电流管电流以在阴影面上向纸面里为正方向,d \Phi 的正方向如图所示
构造如下过程:从0开始逐渐增加电流,在此过程中保持电流的分布形式不变,根据叠加原理,d \Phi 可以看成是无数个小微元电流管叠加产生的,其大小取决于两者的相对位置和电流管内电流大小,于是记
d \Phi = d S \cdot\int_{}^{}\int_{}^{}\alpha\left(r\right) d i \left( 1 \right)
在电流形式不变的前提下, \alpha\left( r \right) 不变,于是可以证明d \Phi 正比于 I ,记
d \Phi = \beta\left( r \right)IdS \left( 2 \right)
\beta\left( r \right) 是一个只和要计算磁通量的微元位置有关的函数。
在电流增加时,磁通量也会增加,并产生感应电动势。沿小电流管积分:
\oint_{}^{}E\cdot dl=-\frac{\partial d\Phi}{\partial t} \left( 3 \right)
电源克服电动势做功为:
dW=di\cdot dt \frac{\partial d\Phi}{\partial t}=di\cdot d\Phi _{r=r_{a}} \left( 4 \right)
d\Phi _{r=r_{a}} 是 r_{a} 处微元磁通量管只对时间的增量,穿过阴影区域的电流管有很多个,对该区域积分有:
dW=id\Phi_{r=r_{a}}=id\left[ \beta\left( r_{a} \right)idS\right] \left( 5 \right)
这只是微元磁通量管对穿入其中的电流产生的做功,对所有磁通量管积分:
dW=\int_{}^{}\int_{}^{}id\Phi=\int_{}^{}\int_{}^{}id\left[ \beta\left( r\right) idS\right] \left( 6 \right)
从 i=0 开始积分:
W=\frac{1}{2}I^{2}\int_{}^{}\int_{}^{}\beta\left( r \right)dS \left(7 \right)
又
W=\frac{1}{2}LI^{2} \left( 8 \right)
如果定义 \Psi=LI ,可以得到:
\Psi=I\int_{}^{}\int_{}^{}\beta\left( r \right)dS \left(9 \right)
把 I 放进去:
\Psi=\frac{1}{I}\int_{}^{}\int_{}^{}Id\left[ \beta\left( r \right) IdS\right]=\frac{1}{I}\int_{}^{}\int_{}^{}Id\Phi \left( 10 \right)
当然也可以在 \left( 4\right) 式到 \left( 5\right) 式上做个手脚,改变积分顺序,可以先算穿过 j 电流环的所有磁通量环对该电流环产生的功:
dW=di\Phi_j=di\int_{}^{}\int_{j}^{} \left[ \beta\left( r_{a} \right)idS\right] \left( 11 \right)
同上可以得到:
\Psi=\frac{1}{I}\int_{}^{}\int_{}^{} \beta\left( r \right) IdSdI=\frac{1}{I}\int_{}^{}\int_{}^{}\Phi dI \left( 12 \right)
证毕 。
参考文献:
- 赵凯华. 也谈“三维导体”的自感系数[J]. 大学物理.
- 1985, 1(3).赵凯华, 陈熙谋. 新概念物理教程.电磁学[M]. 高等教育出版社, 2003.
