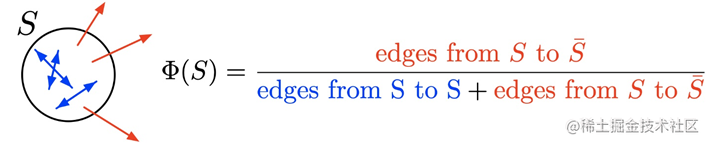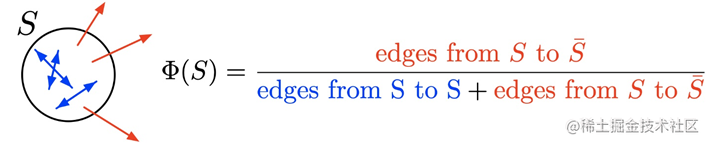1/什么是networkx

有一个关于图论和网络建模的工具叫 NetworkX，
它是用 Python 语言开发的扩展包，内置了常用的图与网络分析算法，可以方便我们进行网络数据分析。
2/社交网络图的增删改查
初始化（构建）一张社交网络图
   # 图的形式有很多种，比如有向图，无向图，多重有向图，多重无向图
   import networkx as nx  
   # 初始化社交网络图，图中没有节点和边关系
   G = nx.Graph() # 无向图，节点之间的边没有方向，且2个节点之间只有一条边
   G = nx.DiGraph() # 有向图，节点之间的边有方向，且2个节点之间只有一条边
   G = nx.MultiGraph() # 多重无向图，边没有方向，两节点之间可以有多条边，不同的边代表不同的意思
   G = nx.MultiDigraph() # 多重有向图，边有方向，两节点之间可以有多条边，不同的边代表不同的意思
   # 添加单个节点
   G.add_node("node_name") 
   # 一次性添加多个节点，这样没有边关系，则图中只是散落的几个点而已
   G.add_nodes_from( ['b','c','d','e'] )
   # 加环，add_cycle()函数意味着同时添加了节点和边关系
   G.add_cycle(['f','g','h','j'])   
   # 添加节点的同时，还可以添加节点的属性，
   # 一个节点可以有一个或者任意多个属性
   # 节点的属性名称和属性值之间的关系，类似字典dict。属性名称不能重复。
   G.add_node(1,weight=2)    # 增加节点1，节点1权重属性值为2
   G.nodes[1]["age"] = 30    # 给节点1增加age属性
   G.add_node(2,weight=3)    # 增加节点2，同时给节点2添加权重属性为3
   G.nodes[0]["foo"] = "bar" # 添加节点0的同时，也添加了foo属性
   list(G.nodes(data=True))  # 查看节点值及其属性,data=True是返回属性
   # 输出结果：
   [(0, {'foo': 'bar'}), (1, {'weight':2, 'time': '5pm'}), (2, {'weight':3})]
# 每次添加一条边
G.add_edge(2,3)  # 添加一条边2-3，同时也添加了节点
G.add_edge(3,2)  # 如果G是无向图，边3-2与边2-3则是同一条边，只会保留一条边(保留后添加的)
# 一次性添加多条边
# 一次性添加多条边，用add_edges_from()函数，添加边，同时就会把节点添加进去
G.add_edges_from( [(1,2),(1,3),(2,4),(2,5),(3,6),(4,8),(5,8),(3,7)] )   
# 因为是无向图，所以如果边已经存在，则后添加的边会覆盖之前添加的边
# add_edge()和add_edges_from()函数只是添加了边，并没有添加边的属性。
添加边的属性，一条边可以有任意多个属性
给这三条边设置属性score，边的属性单独放在一个字典中dict
G.add_edges_from( [(‘小红’, ‘小黄’, {‘score’:70}),
                   (‘小红’, ‘小青’, {‘score’:80}),
                   (‘小黄’, ‘小青’, {‘score’:90})
单独给一条边添加属性：
   G[node][node]['属性名'] = '属性值'
查看边的所有属性
for (u,v,w) in g.edges(data=True): # data=True是返回属性，若是False则只返回节点
   u 是节点
   v 是节点
   w 是连接uv两个节点的边上的所有属性，是一个字典结构。
添加带有权重的边
批量添加带权重的边(以下三种形式都可以实现)：
G.add_weighted_edges_from([ (‘小红’, ‘小黄’, 7.0), 
                            (‘小红’, ‘小青’, 10),
                            (‘小黄’, ‘小青’, 3)] ) 
#元组中的第三个参数默认为weight属性值
G.add_edges_from([(‘小红’, ‘小黄’, {‘weight’:7.0}),
                  (‘小红’, ‘小青’, {‘weight’:10}),
                  (‘小黄’, ‘小青’, {‘weight’:3})] )
获取节点和边，以及节点和边的数量
G.nodes()
G.edges()            
G.number_of_nodes()   
G.number_of_edges()  
清空网络图
   # 清空网络图
   # 把网络图中的节点和边关系全部删除，网络图还是存在的，是一张空的网络图
   G.clear() 
修改节点的属性，修改边的属性
修改节点的属性：
   G.nodes[0]["foo"] = "bar" 
修改边的属性：
   G.edges[‘小红’,‘小黄’][‘weight’] =10
获得边的属性
如果想读取权重，可以使用get_edge_data方法，它接受两个参数u和v，即边的起止点。
G.get_edge_data(0,1)   
# 输出{'weight': 3.0}，这是一个字典结构
删除节点，删除边
# 删除节点
G.remove_node(node)  
G.remove_nodes_from(['b','c','d','e']) 
# 删除边（注意：真是把边删除了，节点还是存在的）
G.remove_edge(node1,node2)  # 一次删除一条边
G.remove_edges_from([])  # 批量删除多条边
保存社交网络图
nx.write_gml(G,"path_where_graph_should_be_saved.gml")   
# 以.gml作为后缀，
G = nx.read_gml("path_to_graph_graph.gml") 
有向图和无向图之间是可以相互转化的
G1 = G.to_undirected()  # 有向图-->无向图
G1 = G.to_directed()    # 无向图-->有向图
在社交网络图中，给图添加属性
 上图中的例子：
 首先创建一个了含有3个节点的社交网络图
 然后计算图中各个节点的中介中心性，得到的是一个字典格式
 然后通过set_node_attrbutes()函数给社交网络图添加属性
 set_node_attrbutes(g,attr_name,attr_value)"
 该函数有3个参数：
    社交网络g，属性名称，属性值
G.subgraph(nodes) 获得子图
# 从一张总的社交网络图中，指定节点，获得一张子图。
g = nx.path_graph(50) # 创建一张含有50个节点的图
nodes = ['A', 'C', 'B']
subgraph = g.subgraph(nodes)
图于图之间的合并
有2种方式
<1>G3=nx.disjoint_union(G1,G2)
  下图中，虽然把2张社交网络图放在了一站图中，但是公共节点(0,1,2)并没有合并在一起，
  所以这个函数不好
<2>g3 = nx.compose(g1,g2)
  下图中，公共节点已经合并了
nx.path_graph()
G=nx.path_graph(8)
该函数的作用是创建一个含有8个节点的社交网络图，形状类似于单链表的形式
下图只看左边即可
nx.has_path(G,source,target)
# 判断2节点是否连通
import networkx as nx
nx.has_path(G,source,target)
nx.complete_graph()
g=nx.complete_graph(3)
该函数是创建两两相连的社交网络图
下图只看中间即可
通过nx.bfs_successors(g,source=node,depth_limit=depth)
bfs_successors()函数是得到指定节点的所有层次的相邻节点
通过一定的函数改造，可以得到指定节点的指定层次的相邻节点。    
获取结点i的邻居节点
G.neighbors(i)
3/社交网络图的特征
 构建完社交网络图之后，我们可以进行挖掘。
 比如可以挖掘社交网络的直径，coheison，apl，
 针对图中的节点，我们可以挖掘中介中心性，特征向量中心性，紧密中心性，pr值，ppr值等
网络图的直径
diameter_value = nx.diameter(G)
# 网络直径,前提是网络图是联通的(及不能有孤立的节点)
网络直径并不能很好的去刻画网络的特征，一般用有效直径来衡量。
有效直径指的是；
   在该直径d下，90%以上的节点都是连通的
    import networkx as nx
    G = nx.DiGraph()
    G.add_nodes_from( nodes )
    G.add_edges_from( edges )
    diameter_value = nx.diameter(G) 
度中心性(不经过归一化处理)：
dict( G.degree ) 
该指标是针对网络中的节点来说的，就是其一度连接点。
如果是有向图的话，还分为出度和入度（由自己指向别人的，和由别人指向自己的）
一个节点的度: 就是其一度连接点的数量，dict( G.degree )该函数没有经过归一化处理
设想一下，你的微信账号，是不是意味着微信好友数量越多，那么你的社交圈子越广？
比如我有20个好友，那么意味着20个节点与我相连。
如果你有50个好友，那么意味着你的度中心性比我高，社交圈子比我广。
这个就是度中心性的概念。
当然，刚才这个情况是无向图的情形，如果是有向图，需要考虑的出度和入度的问题。
import networkx as nx
G = nx.Graph()
G.add_nodes_from(nodes)
G.add_edges_from(edges)
result = dict( G.degree )  # 得到一个字典,里面是每一个节点的度中心性
G.degree(node_name)这样得到的是单个节点的度中心性
这样得到的也是网络中每个节点的度中心性，只是没有进行归一化的处理
度中心性(经过归一化处理)：
nx.degree_centrality(G)  
# 该函数经过了归一化处理，就是度中心性/(n-1),如果没有循环的话，度中心性的取值范围就是[0,1]
通过节点的度表示节点在图中的重要性，默认情况下会进行归一化处理，其值表达为节点度d(u)除以n-1
其中n是网络中节点的数量，n-1就是归一化使用的常量
这里由于可能存在循环(这里的循环指的是节点指向自身)，所以该值可能大于1.
中介中心性：betweenness_centrality
比如社交达人，我们认识的不少朋友可能都是通过他/她认识的，这个人起到了中介(桥梁)的作用，
中介中心性指的是：在一个网络中，一个节点在其他2个节点的最短路径上的次数，次数越多，中介中心性越大。
如果这个节点的中介中心性高，那么它对整个网络图的转移会有很大的影响，
如果中介中心性大的节点从网络中移除，则可能会出现结构洞。
考察的是某个节点对网络中其他节点信息传播的控制能力，
换句话说：就是这个节点相当于一个闸，和它相连的节点想要连接其他节点，都必须经过它。
衡量的公式：
如果要考虑标准化/归一化的问题，可以用一个节点承担最短路桥梁的次数除以所有的最短路径数量。
在无向图中，该值表示为节点作占最短路径的个数除以(n-1)*(n-2)/2
在有向图中，该值表达为节点作占最短路径个数除以(n-1)*(n-2)
import networkx as nx
G = nx.DiGraph()
G.add_nodes_from([])
G.add_edges_from([[],[],[]...])
dict1 = nx.betweenness_centrality(G)  
# 得到一个字典结构，字典中是每一个节点的中介中心性的值。
特征向量中心性: eigenvector_centrality
一个节点的特征向量中心性与其临近节点的中心性得分的总和成正比。
与重要的节点连接的节点更重要，有少量有影响的联系人的节点其中心性可能超过拥有大量平庸的联系人的节点。
也就是说：朋友不在于数量多，而在于朋友的质量
import networkx as nx
G = nx.Graph()
G.add_nodes_from(node_names)
G.add_edges_from(edges)
result = nx.eigenvector_centrality(G)  # 得到一个字典格式
# 得到某个节点的该指标值
result.get(node,None)
紧密中心性：closeness_centrality
紧密中心性反映在网络中某一节点与其他节点之间的接近程度，
衡量公式：
   将一个节点到网络中其他所有节点的最短距离累加起来，其倒数表示接近中心性。
对于一个节点，它距离其他节点越近，那么它的紧密中心性越大。
紧密中心性需要考量每个节点到其他节点的最短路径的平均长度，
也就是说，对于一个节点而言，它距离其他节点越近，那么它的中心度越高。
针对节点，通过距离来表示节点在图中的重要性，一般是指节点到其他节点的平均路径的倒数，
这里还乘以了n-1（n是网络中节点的数量）。该值越大表示节点到其他节点的距离越近，即中心性越高。
nx.closeness_centrality(G)    # 得到一个字典格式
沟通充分程度:cohesion
 计算公式： 网络中实际存在的边数量 / 网络中可能存在的边数量
 一个网络最多可能存在边数量是： 节点数量 * (节点数量-1) / 2
 网络中的各个节点之间的沟通充分程度，取值范围[0,1],越是接近1，说明这个网络的沟通越充分
 用的是无向网络
 cohesion_value = nx.density(G)
网络的传递性： nx.transitivity(G)
 该指标是针对网络的
 网络传递性表示的是：
     一个图形中节点聚集程度的系数，一个网络有一个值，可以衡量网络的关联性，
     该值越大，表示交互关系越大，网络越复杂。
 即在社交网络中，认识同一个节点的两个节点也可能互相认识双方
 计算公式为：3*图中三角形的个数/三元组个数（该三元组个数是有公共顶点的边对数，这样就好数了）。
average_shortest_path_length()  # 平均途径长度指标
 是针对网络的
 平均途径长度指标：是对一个网络中各个节点之间关联程度的测量，反映了整个网络中各个节点之间的整合程度
 先计算网络中任意2个节点的最短距离，然后计算平均值，作为整个网络的平均途径长度
 取值范围：最小值是1，如果是1，则说明网络中任意2个节点之间都有连接
  G = nx.Graph()
  G.add_nodes_from(node_names)
  G.add_edges_from(edges)
  # 计算average_path_length指标
  average_path_length_value = nx.average_shortest_path_length(G)  # 得到的是一个数值，整个网络的平均最短路径长度
集聚系数：Clustering coefficient
 集聚系数分为整体与局部两种。
 整体集聚系数给出一个图中整体的集聚程度，而局部集聚系数则可以测量图中每一个节点附近的集聚程度。
 也就是说：全局是面向网络的，局部是面向网络中过的节点的
 如何计算全局集聚系数：
    先计算网络中各个节点的集聚系数，然后计算平均值，把这个平均值作为整个网络的全局集聚系数。
    triplet是一个三元组，就是三个节点：
       如果三个节点之间有2条边，就是open triplet，
       如果三个节点之间有3条边，就是closed triplet
 全局集聚系数 = closed triplet /（open triplet + closed triplet）
 局部集聚系数是面向节点的，指的是一个节点的聚聚系数。
      计算当前节点的所有邻居（其一度连接点）之间的实际连边数/可能有的所有连接数   
      对于节点v，找出其一度连接点，计算这N个一度连接点构成的网络中的边数K，
      除以这N个一度连接点一共可能存在的边数量 N *（N-1）/ 2
      1节点的邻居节点（2,3），他们之间构成的边有1条，可能构成的边1条，因此1/1=1
      2节点的邻居节点（1,3），他们之间构成的边有1条，可能构成的边1条，因此1/1=1
      3节点的邻居节点（1,2,4,5），他们之间构成的边有1条，可能构成的边(43)/2条，因此1/6=1/6
      4节点的邻居节点（3），他们之间构成的边有0条，可能构成的边0条，因此0
      5节点的邻居节点（3），他们之间构成的边有0条，可能构成的边0条，因此0
      则，5个节点平均local Clustering coefficient = (1+1+1/6)/5=13/30=0.4333
 虽然，求网络的集聚系数定义为网络中存在的三角形个数 * 3 再除以三元组个数，但是实际中大多采用所有节点聚类系数的平均值来计算。
 local_clustering_dict = nx.clustering(G)  
  # 得到一个字典，格式{"node1":value,"node2":value,,,,} 是网络中每一个节点的局部集聚系数
集聚系数: Clustering coefficient
   集聚系数分为整体与局部两种。
   整体集聚系数给出的是整个网络的集聚程度，而局部集聚系数则可以衡量图中每一个结点附近的集聚程度。
   也就是说：全局集聚系数是面向整个网络的，，局部集聚系数是面向网络中的节点
   当计算全局集聚系数的时候，一般是先计算网络中各个节点的集聚系数，
   然后计算平均值，把这个平均值作为整个网络的全局集聚系数。
   triplet是一个三元组，就是三个节点，
   如果这三个节点之间有2条边，就是open triplet，
   如果三个节点之间有3条边，就是closed triplet
   # 全局集聚系数的计算方法：
   全局集聚系数 = closed triplet /（open triplet + closed triplet）  
  # 局部集聚系数的计算方法：
  如果要计算某个节点的集聚系数(也就是局部集聚系数)
  先找到该节点的所有一度连接点，
  然后计算所有一度连接点之间的实际连边数/可能有的所有连接数   
  对于节点v，找出其直接邻居节点集合N（有N个一度连接点），
  计算这N个一度连接点构成的网络中的边数K，除以这N个一度连接点一共可能存在的边数量N *（N-1）/ 2
      1节点的邻居节点（2,3），他们之间构成的边有1条，可能构成的边1条，因此1/1=1
      2节点的邻居节点（1,3），他们之间构成的边有1条，可能构成的边1条，因此1/1=1
      3节点的邻居节点（1,2,4,5），他们之间构成的边有1条，可能构成的边(43)/2条，因此1/6=1/6
      4节点的邻居节点（3），他们之间构成的边有0条，可能构成的边0条，因此0
      5节点的邻居节点（3），他们之间构成的边有0条，可能构成的边0条，因此0
      则，5个节点平均local Clustering coefficient = (1+1+1/6)/5=13/30=0.4333
  虽然，计算网络的集聚系数定义为网络中存在的三角形个数 * 3 再除以三元组个数，但是实际中大多采用所有节点聚类系数的平均值来当作整个网络的全局集聚系数。
  local_clustering_dict = nx.clustering(G)  #得到一个字典，各个节点的局部集聚系数
  global_clustering_value = nx.average_clustering(G)  # 该公式计算的是平均集聚系数
4/pandas数据结构和networkx时间的关系
 pandas数据对象可以直接转化为networkx社交网络图，
 networkx社交网络图也可以转换为pandas数据结构。
 我不知道这个是否和networkx是python编写的有关系。
pandas与networkx之间的关系
<1>pandas数据类型直接转化为图
   pandas数据中应该至少包含两列节点名称和零列或更多列边缘属性，每一行是一个边缘实例进
   import networkx as nx
   G = nx.convert_matrix.from_pandas_edgelist(df,
                                              source="",
                                              target="",
                                              edge_attr=str或者列表,
                                              create_using=)
   参数如下：
   df: 图的边列表表示法，至少有2列数据(2个节点)
   source: 源节点的有效列名称（字符串或整数）
   target: 目标节点的有效列名称（字符串或整数）
   edge_attr: 边的属性，string或者是列表。如果为True，将添加其余所有列作为属性加入。
              如果None，图中不添加任何边属性。
   create_using: 该函数是用来指定创建什么类型的图，比如有向图，无向图，是可选参数，
                 默认是无向图，default=nx.Graph()   
   demo如下所示：
<2>图转换为pandas
   import networkx as nx
   data_df = nx.to_pandas_edgelist(G, 
                                   source='source', 
                                   target='target', 
                                   nodelist=None, 
                                   dtype=None, 
                                   order=None)
   demo如下所示：
5/nx.pagerank(G)
构建完一张社交网络之后，通过nx.pagerank()方法可以计算网络中每个节点的重要性，即PR值，
所有节点的pr值加起来为1(当然也可以换算成其他的值)，
正如下图所示（节点的pr值与节点的大小成正相关）：
import matplotlib.pyplot as plt
import networkx as nx
G=nx.binomial_graph(10, 0.3, directed=True)
layout = nx.spring_layout(G)
plt.figure(1)
nx.draw(G, pos=layout, node_color='y')
pr=nx.pagerank(G,alpha=0.85) # 阻尼系数，默认是0.85，及从一个节点跳转到另一个节点的概率是0.85
print(pr)
for node, pageRankValue in pr.items():
    print("%d,%.4f" %(node,pageRankValue))
plt.figure(2)
nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color='m',with_labels=True)
plt.show()
上面的是随机生成的一张图，下面的图中节点大小是与其pagerank值成比例的，具体每个节点的pagerank值为：
0,0.1164
1,0.1006
2,0.1251
3,0.1541
4,0.0835
5,0.0835
6,0.0913
7,0.1171
8,0.0746
9,0.0538
nx.pagerank(g, personalization={node: 1})
import networkx as nx
# g是局部网络，node是需要求PPR的节点
# 计算其他节点对1这个节点的重要性
PPR = nx.pagerank(g, personalization={node: 1})
基于PPR的局部社区发现
绕了一大圈终于到正题了，我们可以对PPR局部社区发现过程整理出以下几个要点：
1.  既然PPR能够表示网络中的其他节点对某个节点n的重要性，那么我们就可以按照重要性从高到低的顺序，依次尝试将其他节点拉入n所在的局部社区。
1.  在此过程中如果某个节点的加入使得局部社区被"**强化**"了，我们就将它正式拉进局部社区。
1.  上述过程达到**结束条件**后，局部社区划分完成。
还记得社区发现的主要思路：**使得社区内部连接紧密，社区之间连接稀疏。
那么对于局部社区而言，我们就可以用**电导率**(conductance)来描述局部社区被"强化"的程度，即**当局部社区的conductance减小，局部社区就被认为是"强化"了**，conductance可以描述为：