【翻译搬运】SciPy-Python科学算法库
SciPy库提供了大量有用的函数和类,用来解决各种专业领域的问题。本文翻译自Jupyter nbviewer中的第三讲。首先,介绍了一些特殊函数,如贝塞尔函数,这对物理学问题的计算提供了方便;之后是各种数值积分问题,常微分方程求解问题以及傅里叶变换,这些也可以描述并求解一些诸如复摆运动、阻尼震荡等复杂的物理过程;同时,该库还可以高效处理线性代数问题,如矩阵的运算、特征值和特征向量以及稀疏矩阵的存储和运算;最优化问题,即寻找函数极值和零点的问题,和插值问题,即用多项式拟合曲线的问题,在SciPy库中也可以找到相应的函数;最后介绍了统计上的应用,包括各种分布的密度函数、分布函数及其图像绘制,以及一些统计检验问题。
作者:J.R. Johansson (邮箱:jrjohansson@gmail.com)
译者:一路向上
最新版本的用法介绍见网站 http://github.com/jrjohansson/scientific-python-lectures. 其他相关介绍见 http://jrjohansson.github.io.

简介
SciPy框架建立于低一级的NumPy框架的多维数组之上,并且提供了大量的高级的科学算法。一些SciPy的应用如下:
- 特殊函数 (scipy.special)
- 积分 (scipy.integrate)
- 优化 (scipy.optimize)
- 插值 (scipy.interpolate)
- 傅里叶变换 (scipy.fftpack)
- 信号处理 (scipy.signal)
- 线型代数 (scipy.linalg)
- 稀疏特征值问题 (scipy.sparse)
- 统计 (scipy.stats)
- 多维图像处理 (scipy.ndimage)
- 文件输入输出 ( http:// scipy.io )
这些模块提供了大量的函数和类,可以用来解决各自领域的问题。 在本节中我们将看到如何使用这些子函数包。 我们首先导入scipy程序包:

如果我们只需要用scipy框架中的一部分,我们也可以选择性的导入。例如,只导入线性代数函数包la,我们可以:

特殊函数
大量的数学函数对许多物理问题的计算是非常重要的。SciPy提供了一系列非常广泛的特殊函数。详见 http://docs.scipy.org/doc/scipy/reference/special.html#module-scipy.special.
为了说明指定的特殊函数的用法,我们先看一下贝塞尔函数的使用细节:
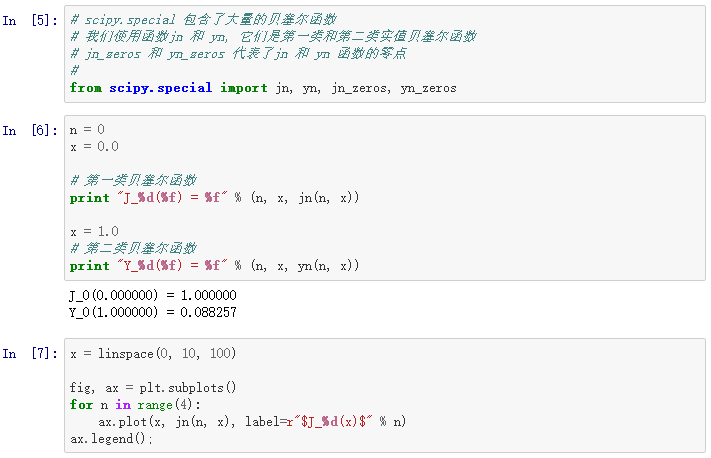
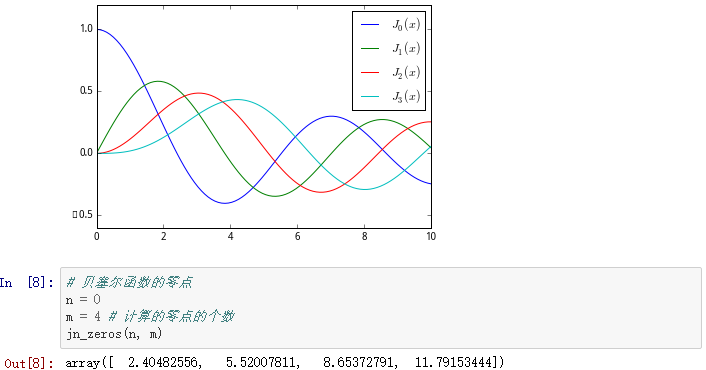
积分
数值积分:求积公式
对f(x)从a到b的积分叫做数值积分,也叫简单积分。SciPy提供了一系列计算不同数值积分的函数,包括quad,dblquad和tplquad,分别包含二重和三重积分。

quad有一系列的可供选择的参数,可以用来调节函数的各种行为(输入help(quad)获取更多信息)。
其基本用途如下:
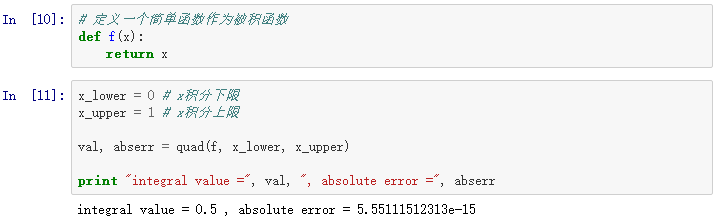
如果我们需要添加更多对于被积函数的参数,可以使用args关键字参数:

对于简单函数而言,对于被积函数,我们可以用λ函数(无名称的函数)来代替清晰定义的函数:
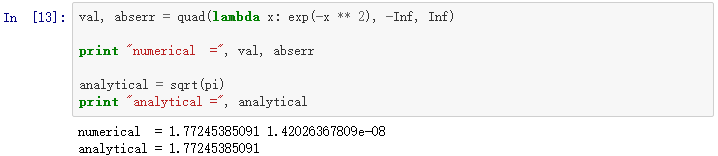
如上所示,我们可以用'Inf'或者'-Inf'作为积分上下限。高维积分用法相同:

注意,我们需要用λ函数对于y积分的极限,因为它们可以看做是x的函数。
常微分方程(ODE)
SciPy提供了两种不同的方法来解决常微分方程:函数odeint的API,和函数类ode面向对象的API。通常odeint比较容易上手,但是ode函数类能够更好的控制函数。
这里我们使用odeint函数,如需了解更多ode函数类的信息,请输入help(ode)。它和odeint很像,但却是面向对象的函数。
使用odeint之前,首先从scipy.integrate中调用它:

常微分方程系通常写作其一般形式:
y' = f(y, t)
其中
y = [y1(t), y2(t), ..., yn(t)]
f的微分是 yi(t) 。为了解决常微分方程,我们需要知道函数 f 和初始条件 y(0) .
高阶微分方程可以通过引进新的变量作为中间变量。
当我们定义了Python函数 f 和数组 y_0 ( f 和 y(0) 都是数学函数),我们调用odeint函数:
y_t = odeint(f, y_0, t)
t是解决ODE问题需要的时间坐标数组,y_t是对于给定点在时间t的一行数组,每一列代表在给定时间t所对应的一个解y_i(t)。我们下面将会看到如何设置f和y_0.
例:复摆
我们考虑一个物理问题:复摆。定义详见 http://en.wikipedia.org/wiki/Double_pendulum.

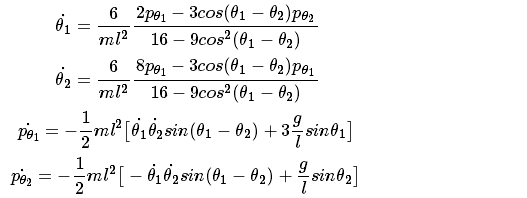
为了让Python代码看起来更简洁,我们引进新的变量,并规定:
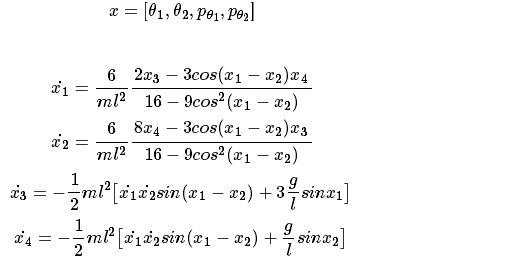

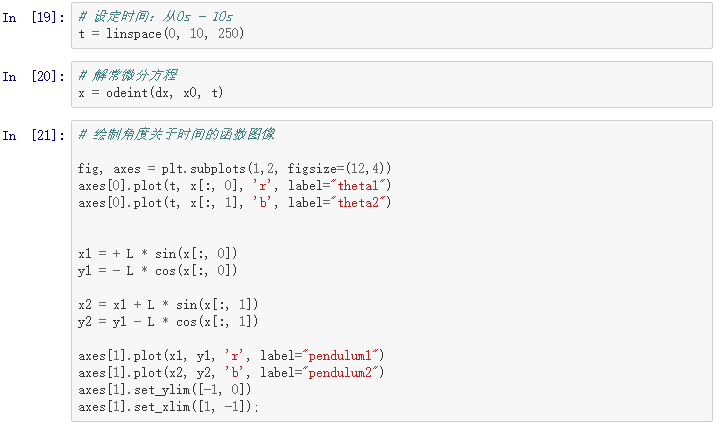
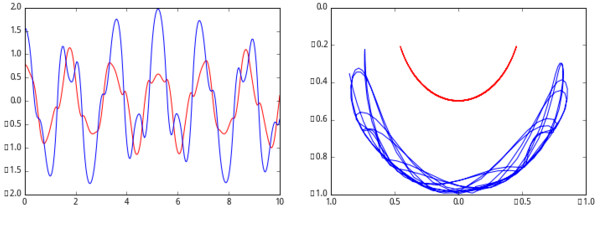
在matplotlib函数的应用中,会介绍如何绘制复摆运动的动图。
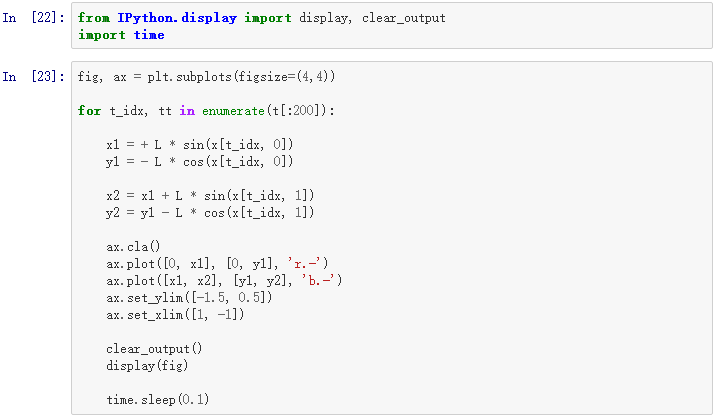

在matplotlib函数的应用中,会介绍如何绘制复摆运动的动图。

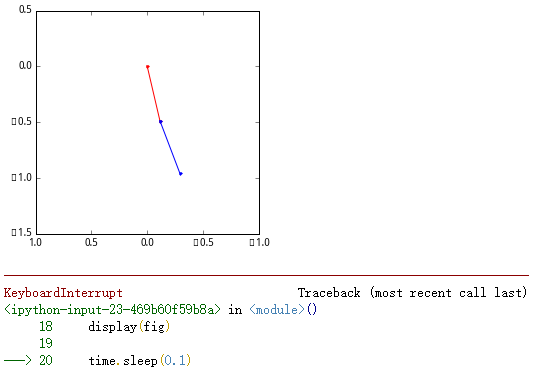
ps:这里的结果不是报错,是因为最后一行代码是每0.1s更新一次状态,为了后面的函数能够正常运行,我把它停掉了。
例: 阻尼谐波振荡器
常微分方程问题对计算物理非常重要,下面我们来看另一个例子:阻尼谐波振荡器。关于概念的解释详见 http://en.wikipedia.org/wiki/Damping.
阻尼谐波振荡器的方程为:
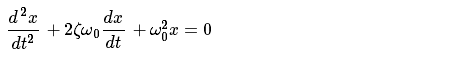
x是振荡器的位置, \omega_{0} 是频率, \zeta 是阻尼比。为了写出标准形式的二阶常微分方程,我们引入 p=\frac{dx}{dt} :
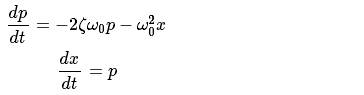
在这个例子中,我们将为常微分方程等号右边的函数添加额外的参数,而不是像前面的例子那样使用全局变量。作为等号右边函数的额外参数的结果,我们需要将一个关键字参数args传递给odeint函数:


傅里叶变换
傅里叶变换是计算物理中的一种通用工具,它在不同文章中都会反复出现。SciPy提供能够从NetLib中接入经典FFTPACK库的函数,它是由FORTRAN语言编写的一个行之有效的FFT库。SciPy API有一些额外的便利功能,但总的来说,API和原来的FORTRAN库密切相关。
为了调用fftpack,请输入:

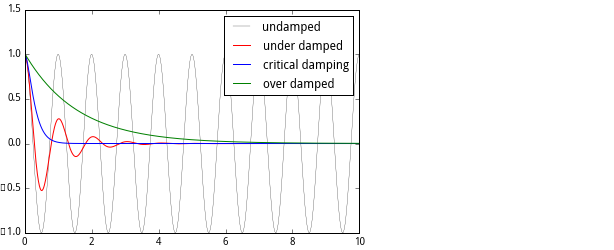
为演示如何用SciPy做一个快速傅里叶变换,让我们来看看用FFT如何解决之前讨论的阻尼震荡问题:
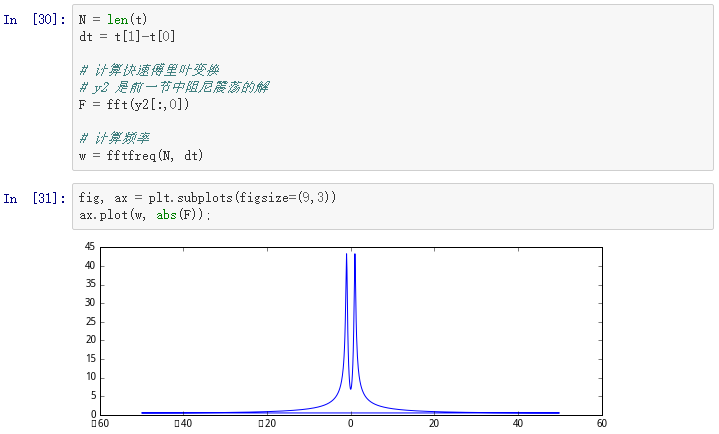
由于信号是实数,所以谱线图是对称的。我们因此只需要画出对应正频率的部分。为了提取w和F的部分,我们可以运用NumPy库:
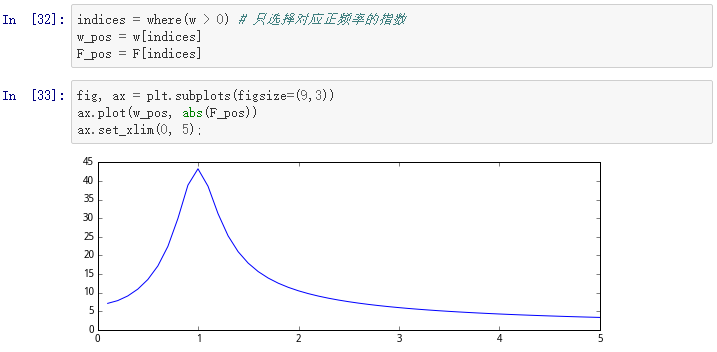
和预期一样,我们看到谱线图在1处达到最高点,这正是在阻尼震荡这个例子中所采用的频率。
线性代数
线性代数部分包含了许多矩阵函数,包括线性方程的解,特征值的解,矩阵函数(例如矩阵指数函数),许多不同的分解(SVD,LU,cholesky)等等。详见: http://docs.scipy.org/doc/scipy/reference/linalg.html.
下面我们看看如何使用这些函数:
1、线性方程组
线性方程组的矩阵形式:

A是矩阵,x,b是向量。可以求解如下:
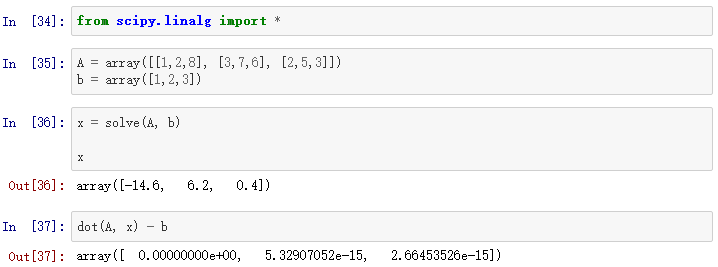
我们也可以:

这里A,B,X都是矩阵:
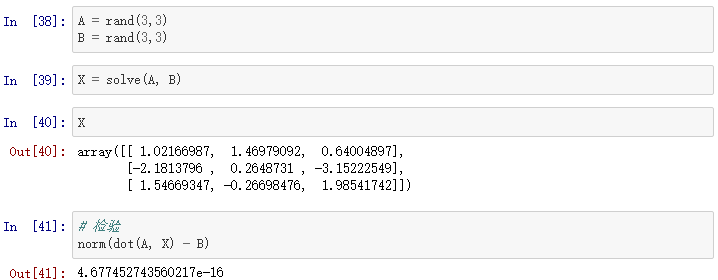
2、特征值和特征向量
矩阵A的特征值问题是:

这里 v_{n} 是第n个特征向量, \lambda_{n} 是第n个特征值:
用eigvals计算矩阵的特征值,用eig计算特征值和特征向量:
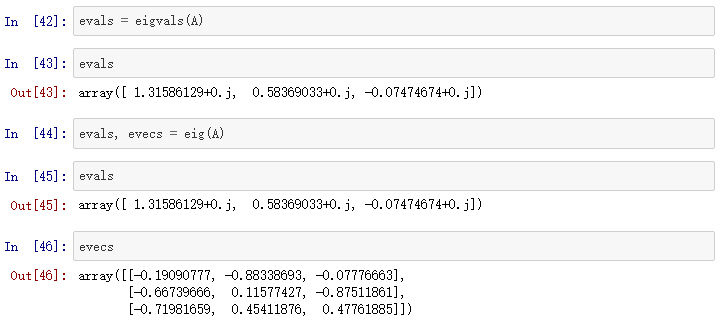
第n个特征值(储存在evals[n]中)对应的特征向量是evecs的第n列,也就是evecs[:,n]. 为了验证它,我们尝试把矩阵和特征向量相乘,并与特征向量和特征值的乘积做比较:

还有许多其他的特殊的本征解,如埃尔米特矩阵(用eigh实现)
3、矩阵运算
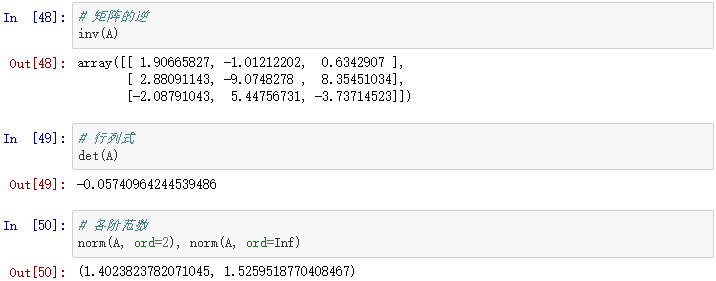
4、稀疏矩阵
稀疏矩阵在处理巨型系统的数值模拟时非常有用,如果描述该问题的矩阵或向量大部分的元素为0。Scipy对于稀疏矩阵有很多处理方法,包括基础的线性代数处理(包括解方程,计算特征值等等)
许多方法都能有效存储稀疏矩阵,一些常用的方法包括坐标形式(COO),列表的列表形式(LIL),压缩稀疏列(CSC)和压缩稀疏行(CSR)。每种方法都有优势和不足。大多数的计算算法(解方程,矩阵和矩阵相乘等等)都能用CSR或者CSC形式处理,但是它们并不直观,也不太容易进行初始化。所以通常来说,稀疏矩阵采用COO或者LIL进行初始化(我们可以在稀疏矩阵中有效添加元素),然后再转换为CSC或者CSR并进行计算。
更多关于稀疏矩阵的信息,详见: http://en.wikipedia.org/wiki/Sparse_matrix.
当我们创建了一个稀疏矩阵,我们要选择其存储形式,如:
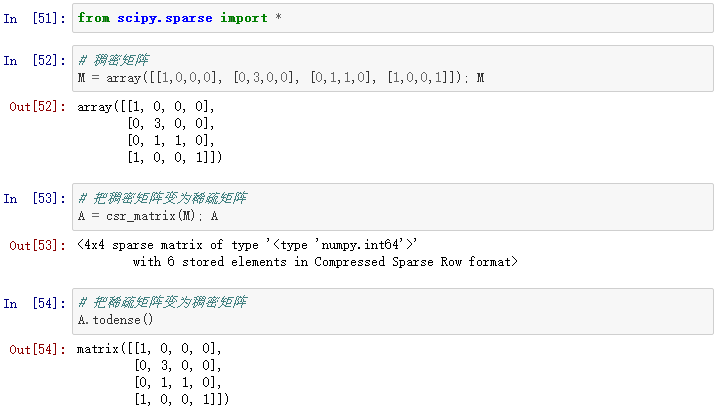
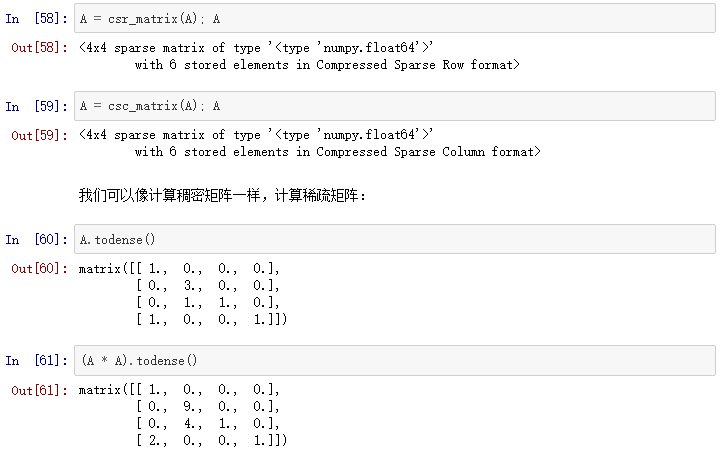
创建稀疏矩阵更有效的方法是,建立一个空矩阵,并用所在矩阵的位置填充(避免创建大的稠密矩阵):

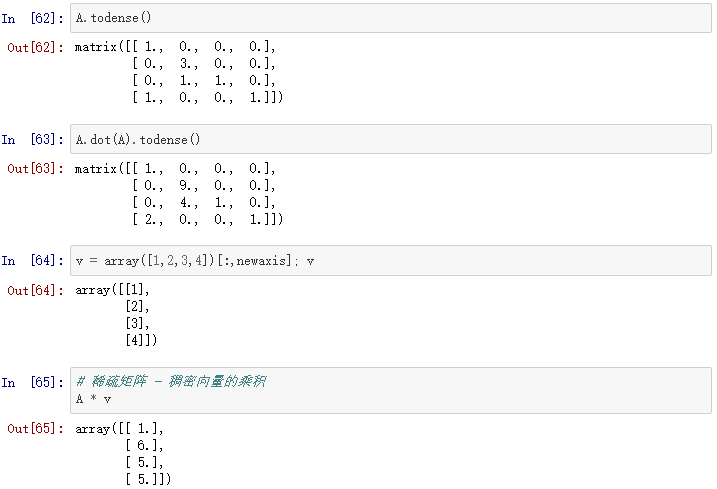

最优化
最优化问题(寻找函数的最大值或者最小值)是数学的一大领域,复杂函数的最优化问题,或者多变量的最优化问题可能会非常复杂。下面我们看一些很简单的例子,更多详细的对于使用SciPy处理最优化问题的介绍,请见: http://scipy-lectures.github.com/advanced/mathematical_optimization/index.html.
首先调用optimize:

寻找最小值
首先我们看如何寻找单变量的简单函数的最小值:

我们可以用fmin_bfgs寻找函数的最小值:
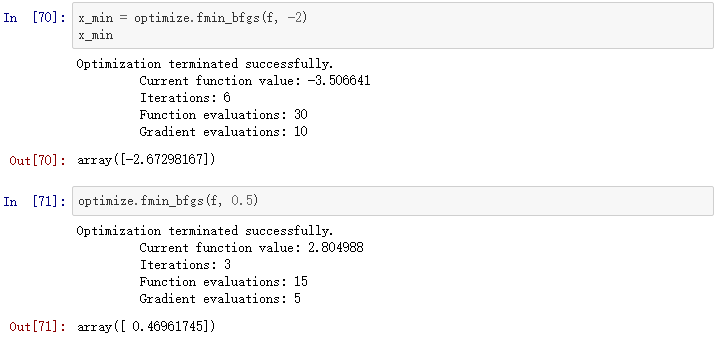
我们还可以用brent或者fminbound函数,它们采用了不太一样的语法和算法。

寻找函数的解
为了寻找函数f(x) = 0 的解,我们可以用fsolve函数,它需要一个初始的猜测值:

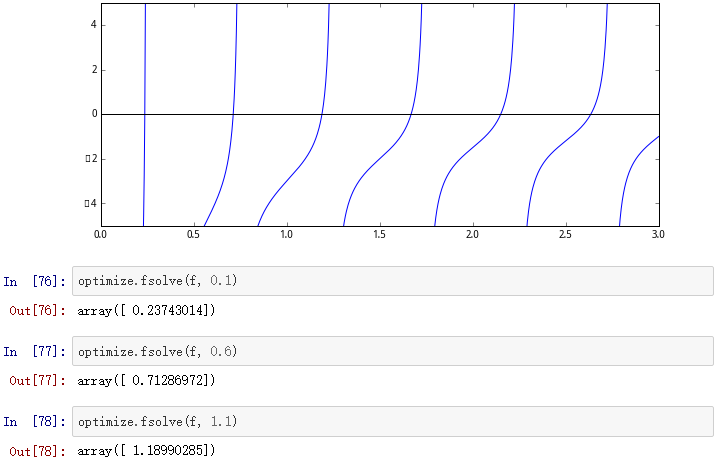
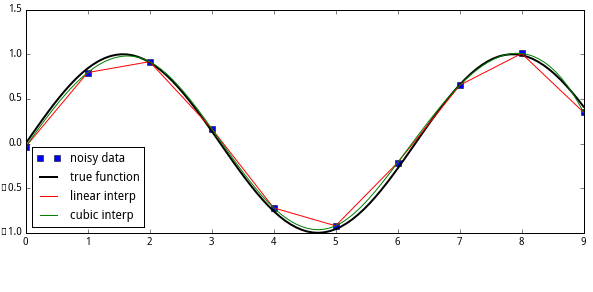
插值
插值在SciPy中能够很容易和方便的实现:interpid函数,当描述X和Y的数据时,返回值是被称之为x的任意值(X的范围)的函数,同时返回相应的插值y:

统计
scipy.stats包含了许多统计分布,统计函数和检验。完整的功能请见: http://docs.scipy.org/doc/scipy/reference/stats.html.
还有一个非常强大的统计模型的包叫做statsmodels,详见: http://statsmodels.sourceforge.net.

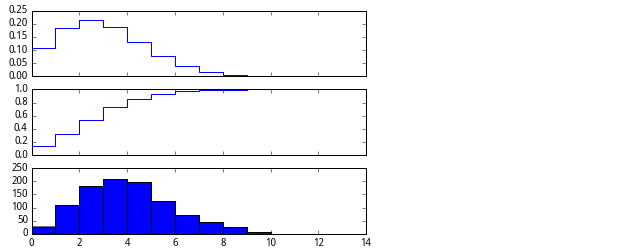
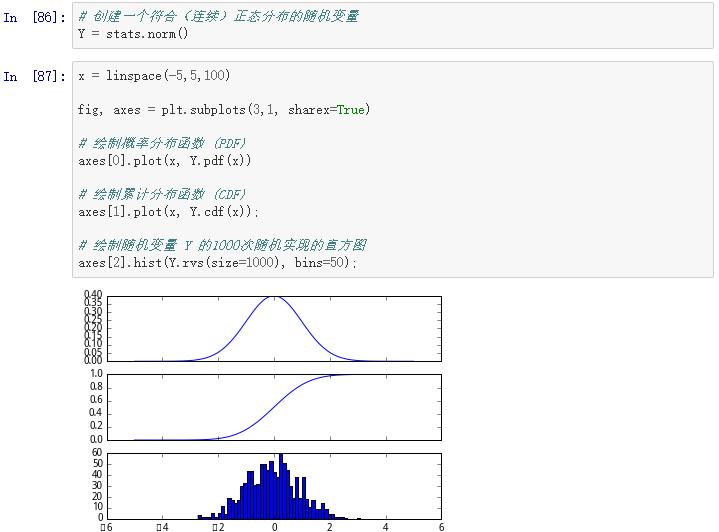
统计结果:

统计检验
检验两组(独立)随机数据是否来自同一个分布:

因为p值很大,我们不能拒绝原假设(两组随机数据有相同的均值)。
为了检验单个样本的数据是否均值为0.1(实际均值为0.0):

p值很小,意味着我们可以拒绝原假设(Y的均值为0.1)。

延伸阅读
http://www. scipy.org - SciPy的官方网页
http:// docs.scipy.org/doc/scip y/reference/tutorial/index.html - SciPy的一个教程
https:// github.com/scipy/scipy/ - SciPy源代码.
版本

到JoinQuant查看原文并参与讨论: 【翻译搬运】SciPy-Python科学算法库

