两个极简的卡尔曼滤波例子
一、概述
卡尔曼滤波,一个很神奇的存在,本人刚接触,理解有限,拿两个书上的例子共享一下。
“卡尔曼滤波器是一个获得估计estimate的计算机算法”。
首先给出卡尔曼滤波的计算过程,其是一个迭代计算的过程。其输入是测量值measurement,输出是估计estimate。卡尔曼滤波器包括两个过程,一个是预测prediction,另外一个是估计estimation。
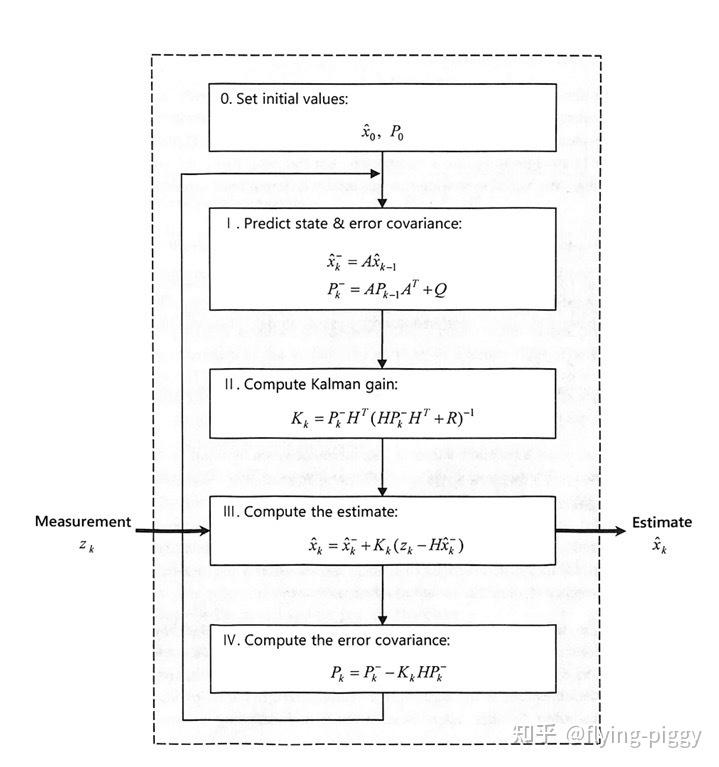
再给出各个变量的含义,其中上标“-”表示预测值prediction(先验priori),这也是其与估计estimate(后验posteri)的区别。
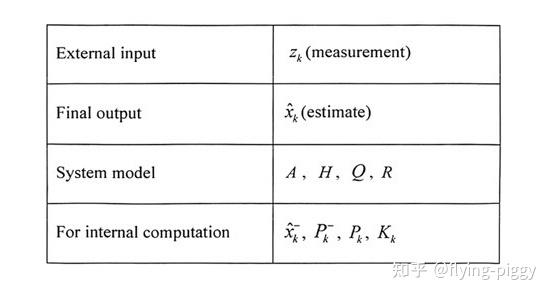
其中,系统模型
- A——决定系统随时间如何变化;
- H——表示测量值与系统状态之间的关系;
- Q和R分别代表对角的协方差矩阵。
- 如果性能不满意,这四个矩阵是唯一的可以调整的因素。

接下来给出概括性的卡尔曼滤波步骤:

二、一个极简例子
接下来就举一个例子,来源于一个测量电压的问题,存在较大噪声。
本例子的目的是移除测量噪声。

系统模型如下,其中噪声符合正态分布。
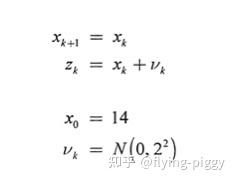
进而得到计算所用矩阵:
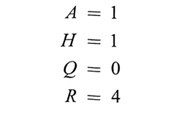
设置初值:

接下来给出卡尔曼滤波的m文件:

进一步对其中主要代码进行解释:

编写测试文件:

假设原始测得的电压如下:

最后,得到滤波后的结果:
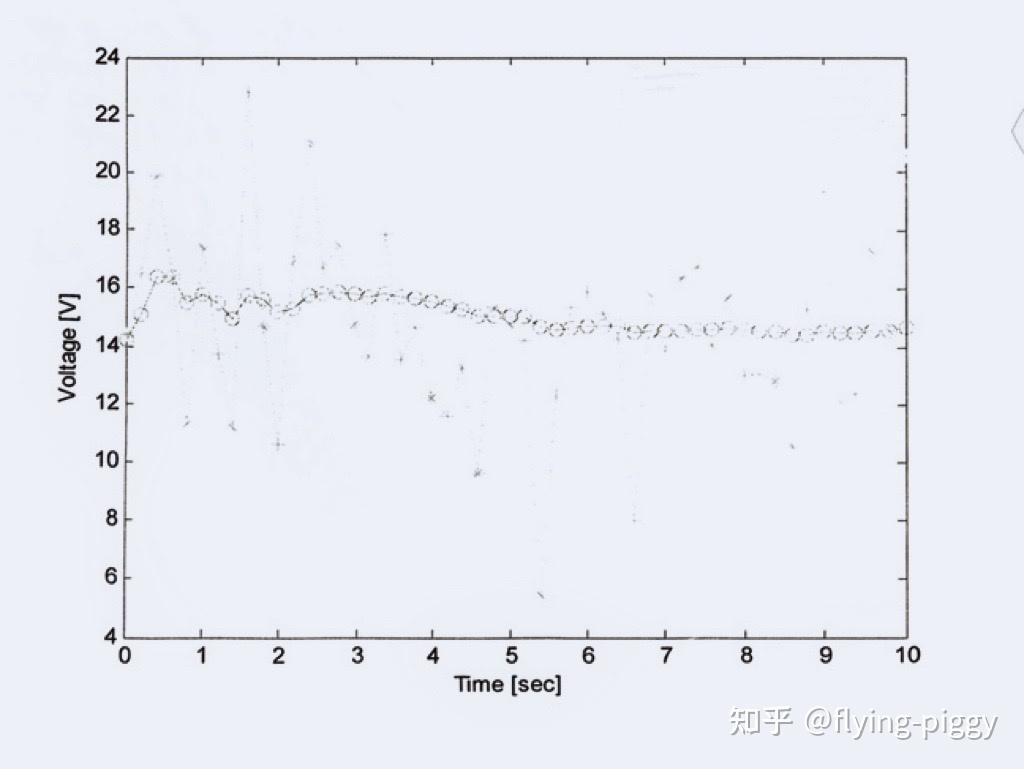
是不是很神奇?
作者其实先介绍的一阶滤波器,有兴趣的参考一下。
三、另外一个例子
上面的例子其实相当于对简单信号的滤波,用一阶滤波器也可以实现,接下来举一个一阶滤波器无法实现的例子。
本例子的目的是使用位置信息估计速度,之所以不用位移除以时间是因为存在噪声,位移存在锯齿。如果采用取多个点的平均,这样的算法复杂且不简洁。

系统模型如下:

协方差矩阵如下:
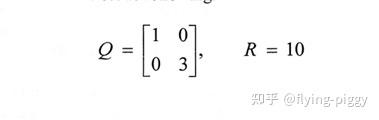
卡尔曼滤波主程序如下:

测试程序如下:

获得原始位置信号程序如下:

结果如下:
位置的估计由于去掉了噪声变得更加光滑。
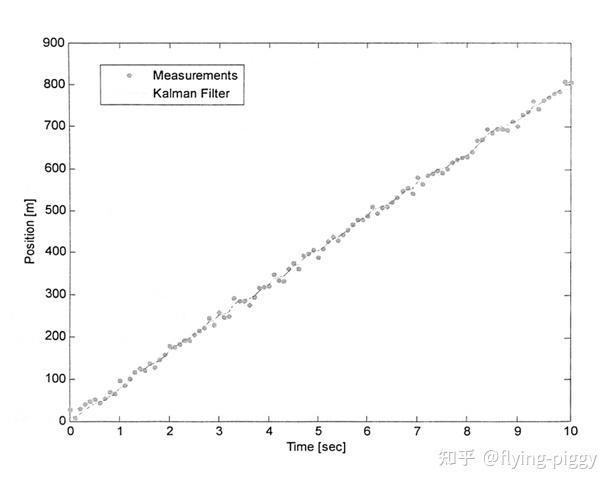
以下是速度的估计,应该是和带有噪声的速度做对比吧?初始速度20是我们人为设置的。
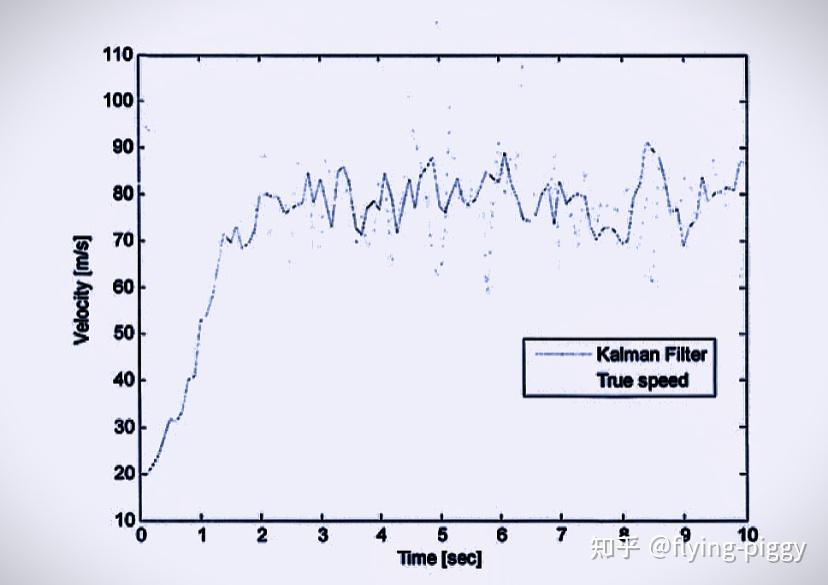
Isn’t this amazing?
光用位置和卡尔曼滤波算法就得到了相当准确的速度,这也是和一阶滤波器不同的地方!
四、多说几句
- 卡尔曼增益K的下标k表示第k次的增益,每次不一样。
- 协方差表示真实值(不可能知道)与估计之间的关系。
- A和Q是预测的关键,如果他们与实际系统不一样,预测的结果会不准确,进而之后的估计也不对。卡尔曼滤波器的性能由系统决定。
- 如果你想让测量值影响小,让估计的结果变化小,那么增加R,减小Q,同时卡尔曼增益也变小了。
- 最难和最重要的是系统模型的推导。
五、参考文献
PHIL KIM.
Kalman Filter for Beginners: With MATLAB Examples
PS.第一次编辑,太烂了,不是我的风格,手边没电脑,不好意思。
刚刚看了B站也有讲解,可以去看看:
【从放弃到精通!卡尔曼滤波从理论到实践~-哔哩哔哩】 https:// b23.tv/MrPR3Xl
