图神经网络GNN的表达能力【斯坦福CS224W】

Cold

神经网络的表达能力

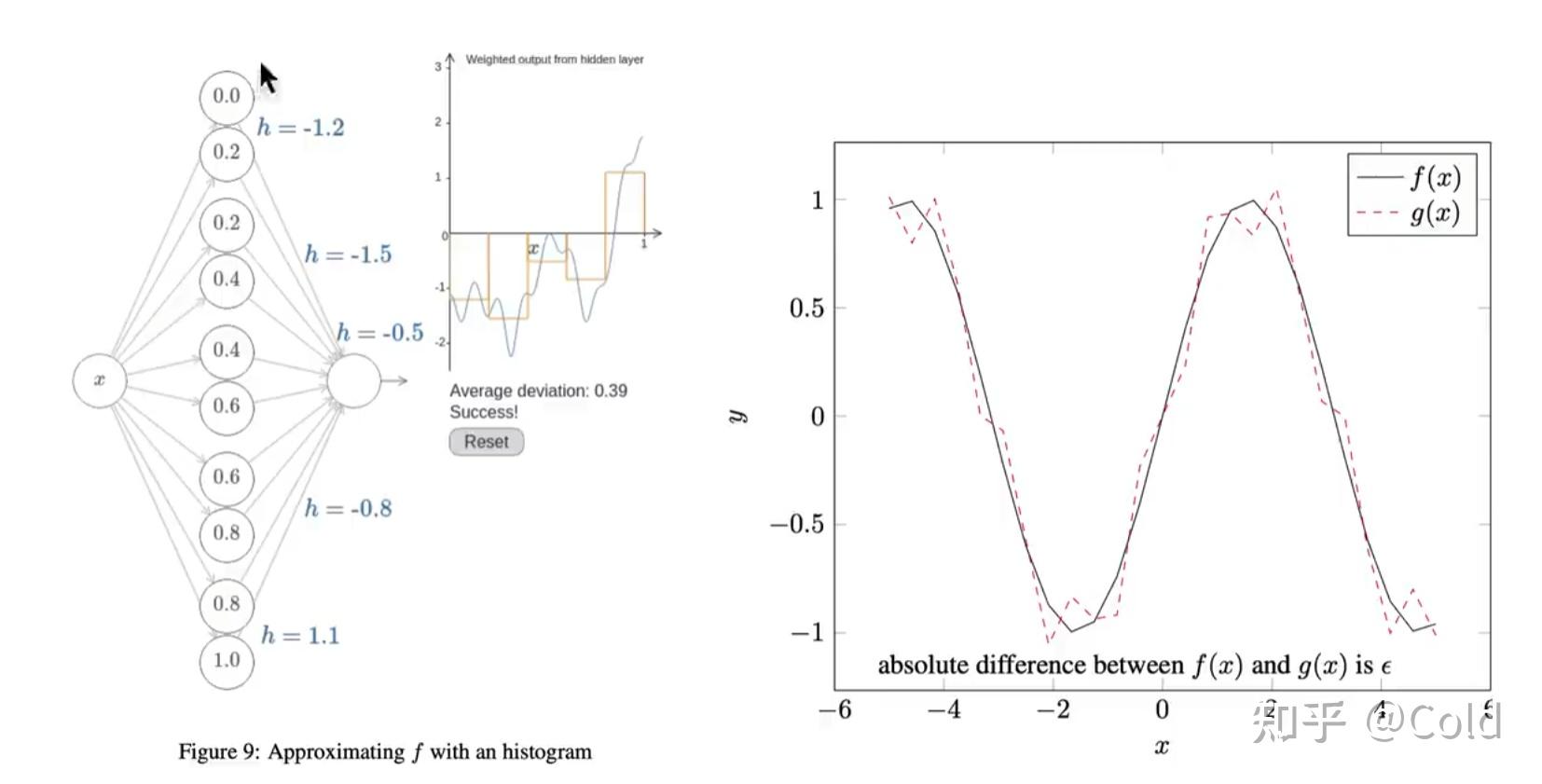
根据万能近似定理，从理论上来说一层隐含层，就可以无限逼近任何一个连续函数。

如下图所示，我们可以发现其可以拟合很多复杂的函数。当然我们深度神经网络，不只是用单一的层来实现，因为仅用一层表示复杂的情况所需的参数量过大，更深的网络可以以更少的参数来表征。

对于图像分类问题，可以将图像表示为向量，嵌入到 D 维空间中去，找到可分的决策边界。

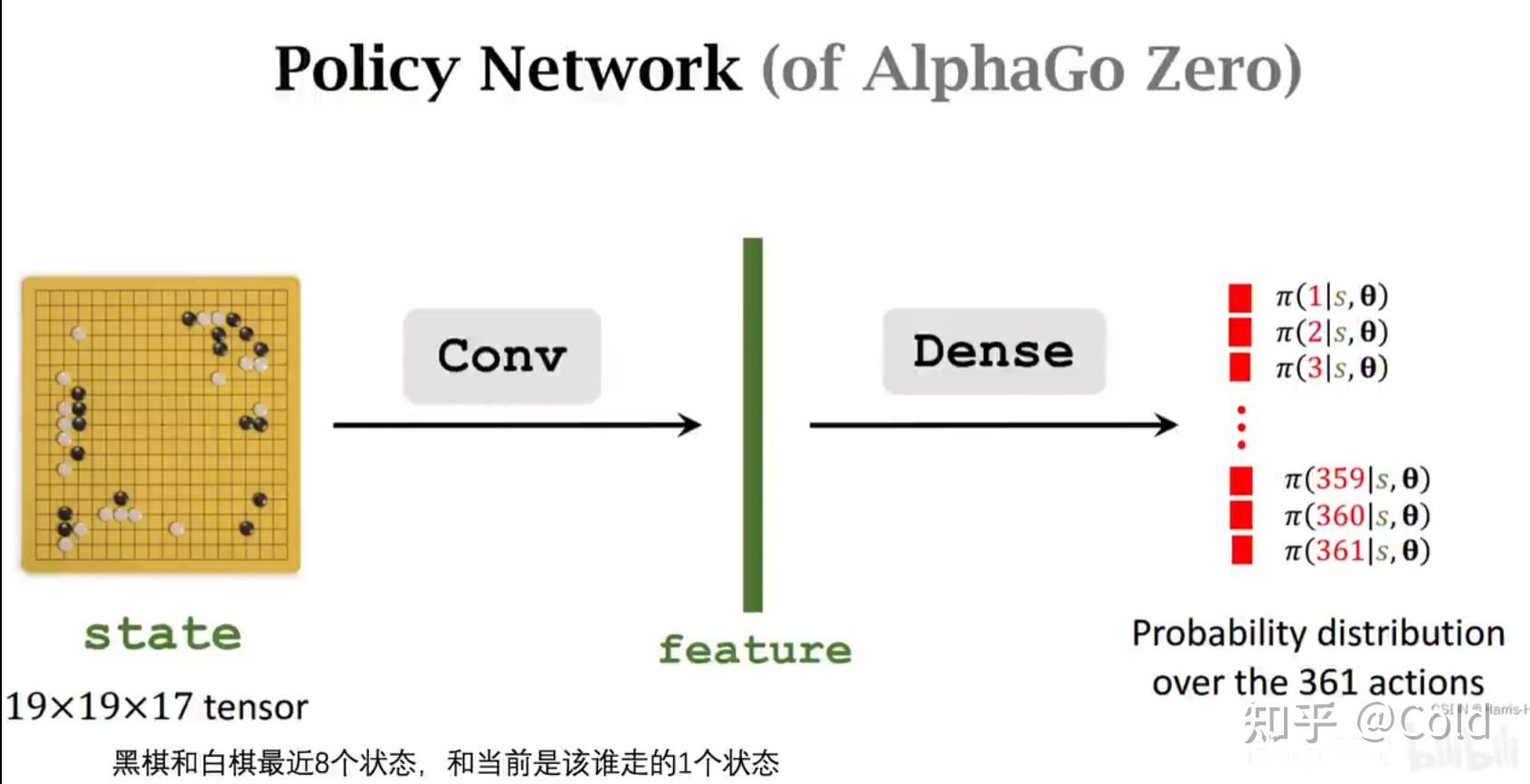
对于强化学习来说，神经网络仍然可以对海量的决策空间，进行搜索。

图神经网络GNN的表达能力

什么是图神经网络的表达能力？能够区分不同的图结构的能力

首先回顾一下，消息传递图神经网络的通用框架，首先在邻域范围内进行消息传递，然后对消息进行聚合（聚合中消息的顺序是无关的）

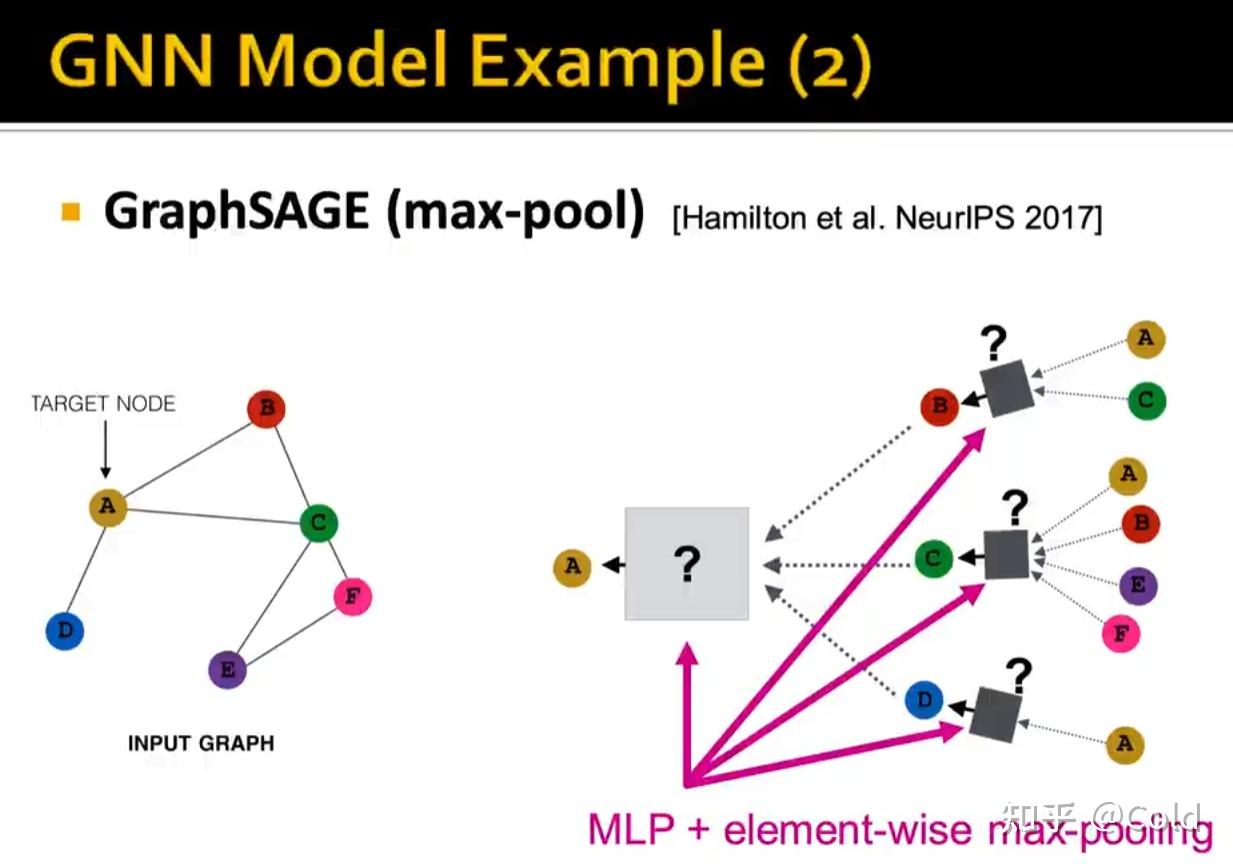
不同模型的消息传递函数，聚合函数都是有所区别的，特别是聚合函数。对于GraphSAGE来说，聚合函数采用的对逐元素做最大池化。

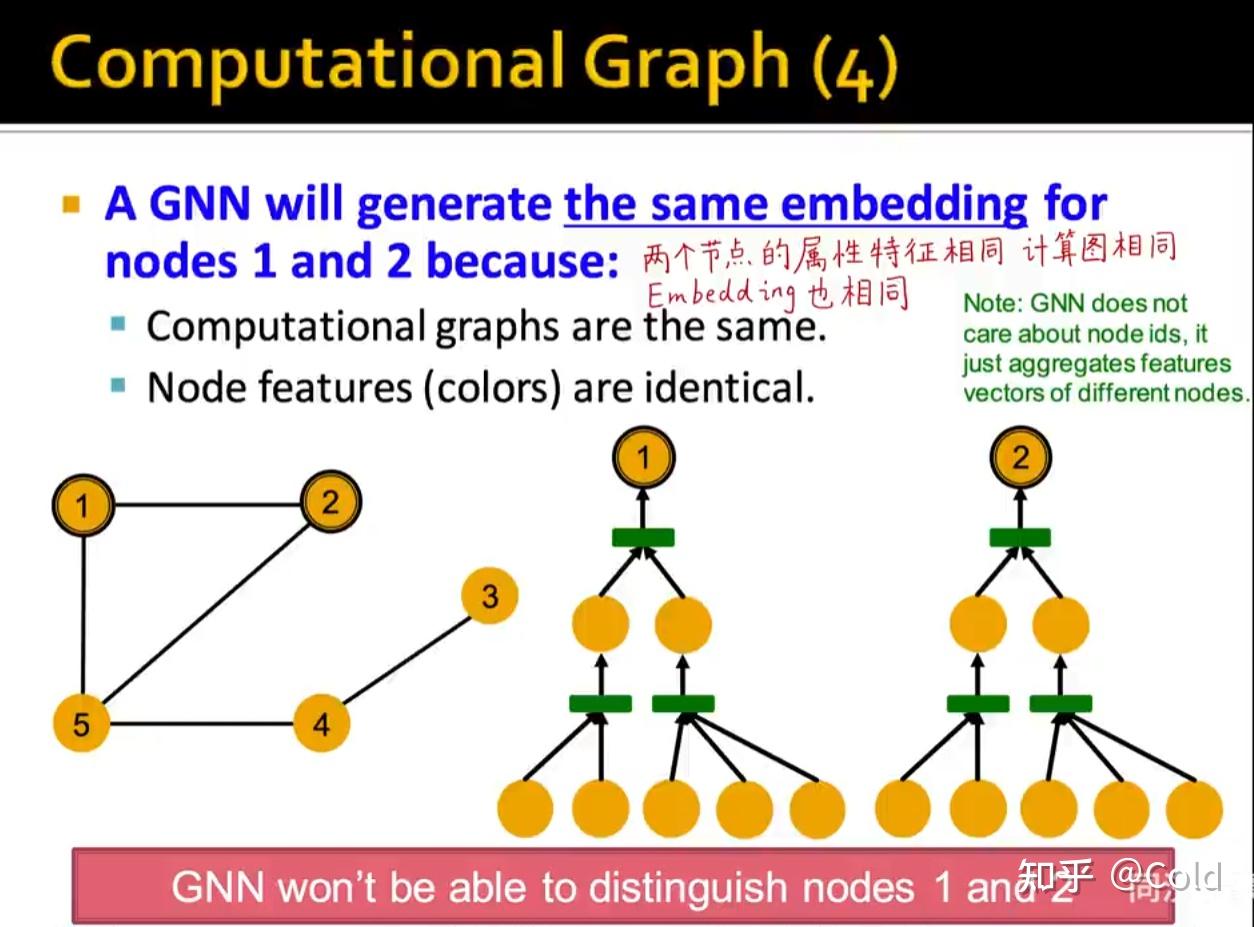
我们用不同的颜色来表示Embedding，初始化阶段，我们将所有的节点初始化为同样的Embedding，我们希望构建计算图，让GNN仅通过连接结构来区分不同的节点（从而展现其表达能力）

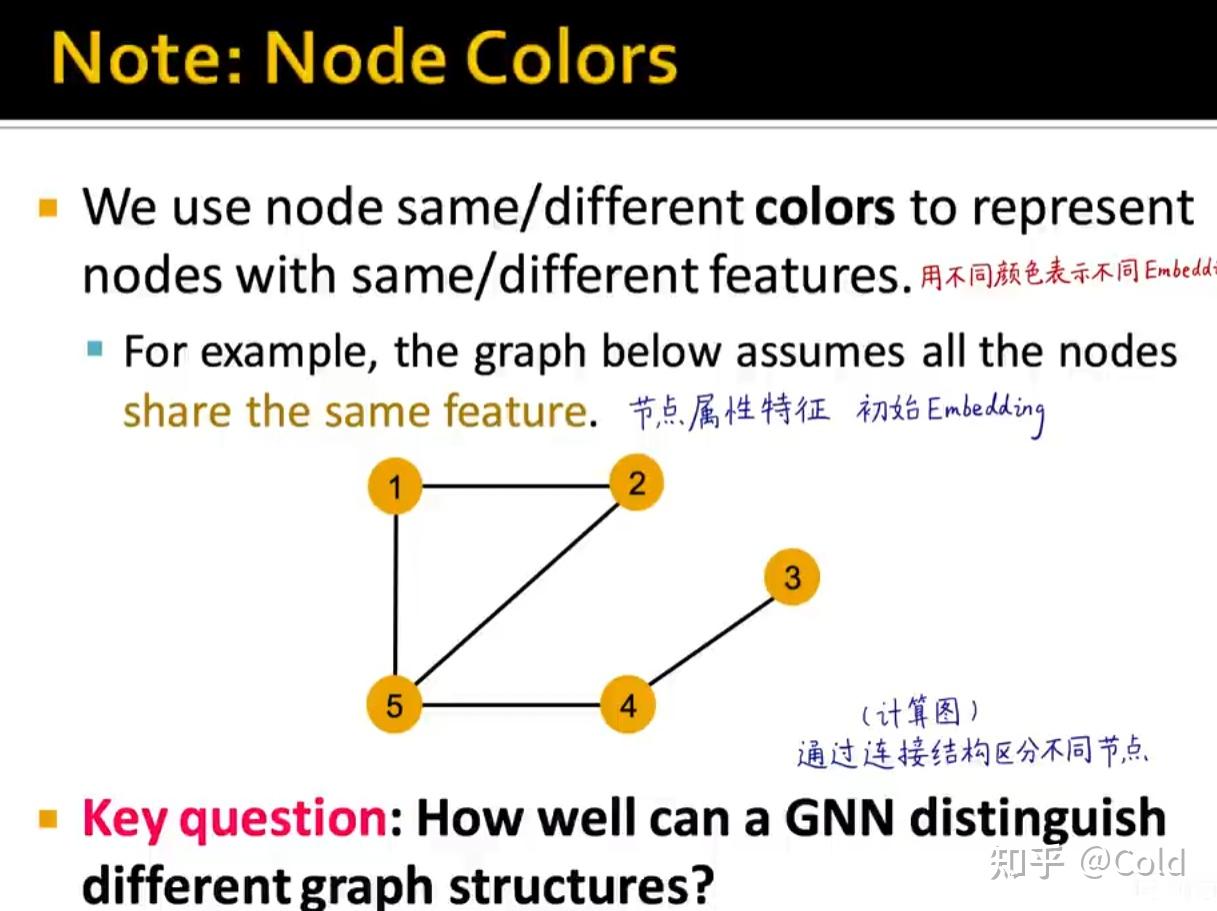
我们可以看到其表示能力是非常强的，构建计算图的时候可以捕获到各类信息，哪怕只利用连接数信息，也可以对节点进行区分。

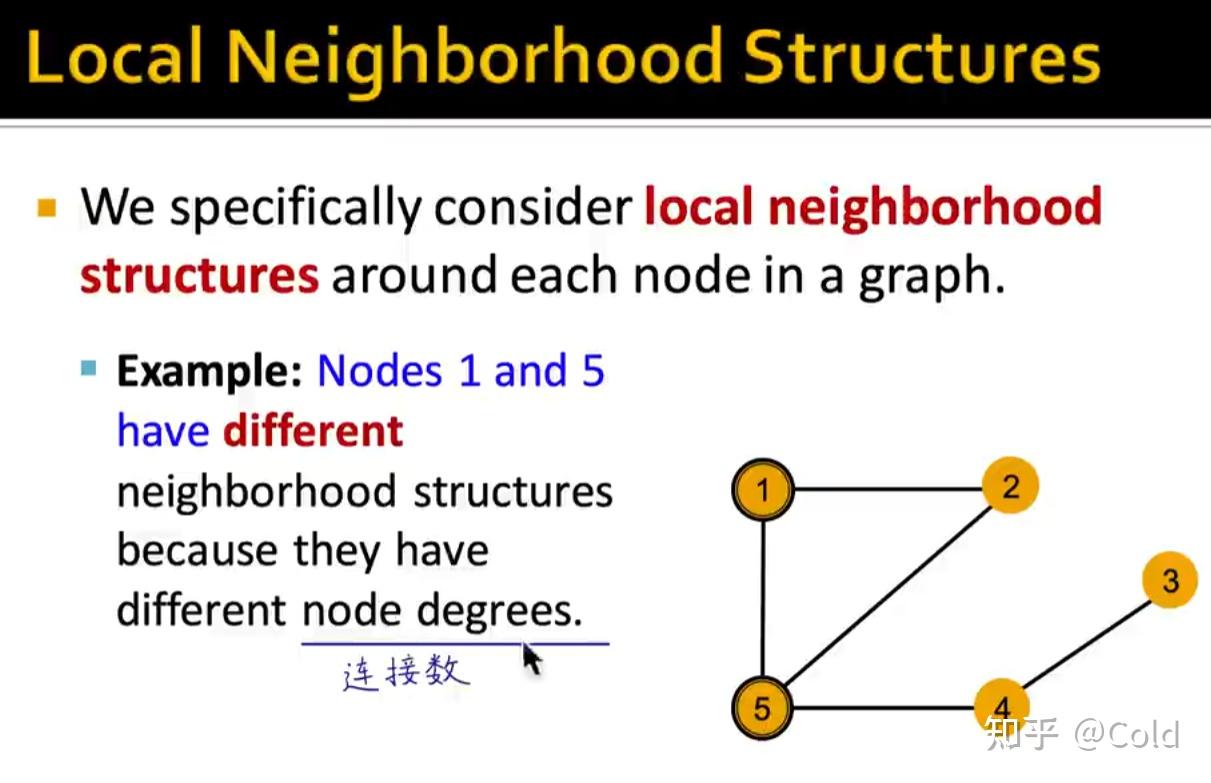
邻居的连接数

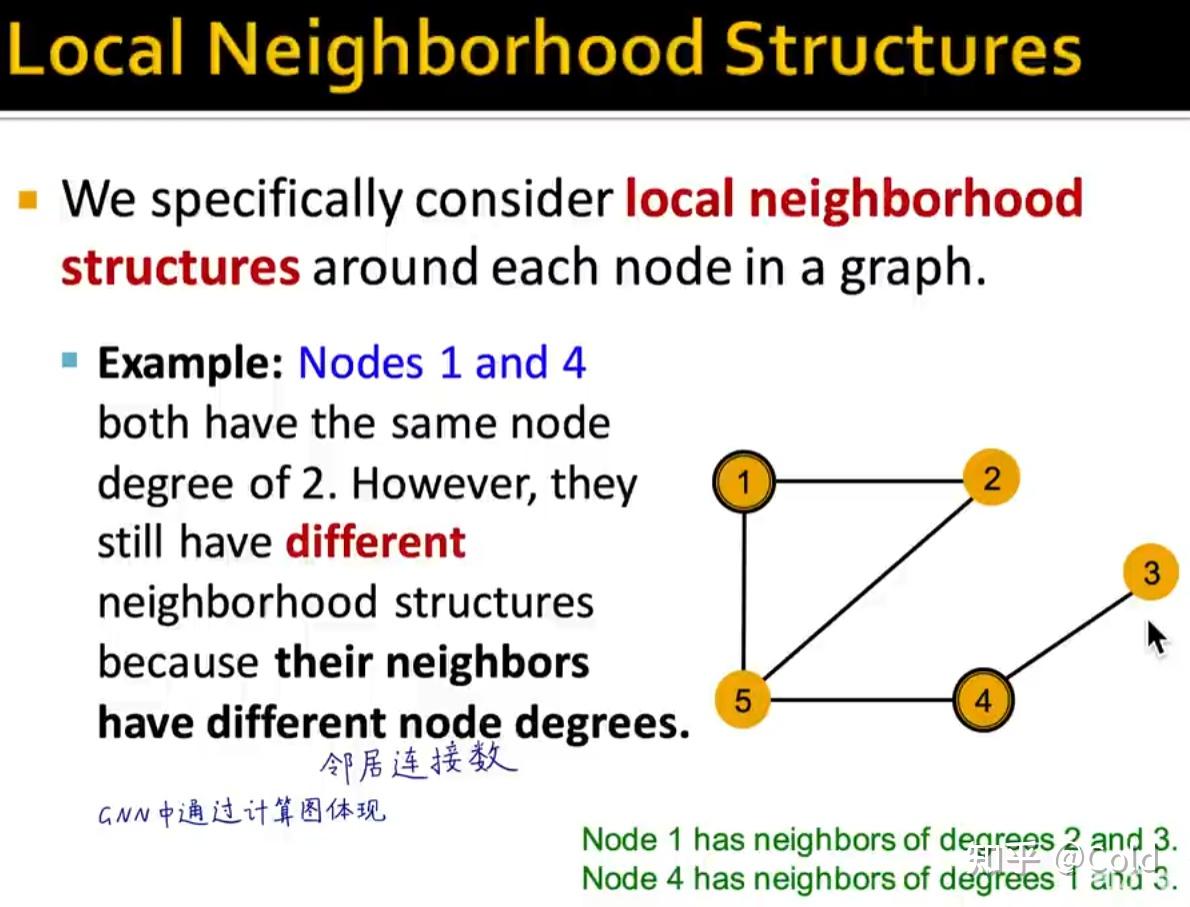
当然仅通过图的连接信息，没有办法区分同形的结构

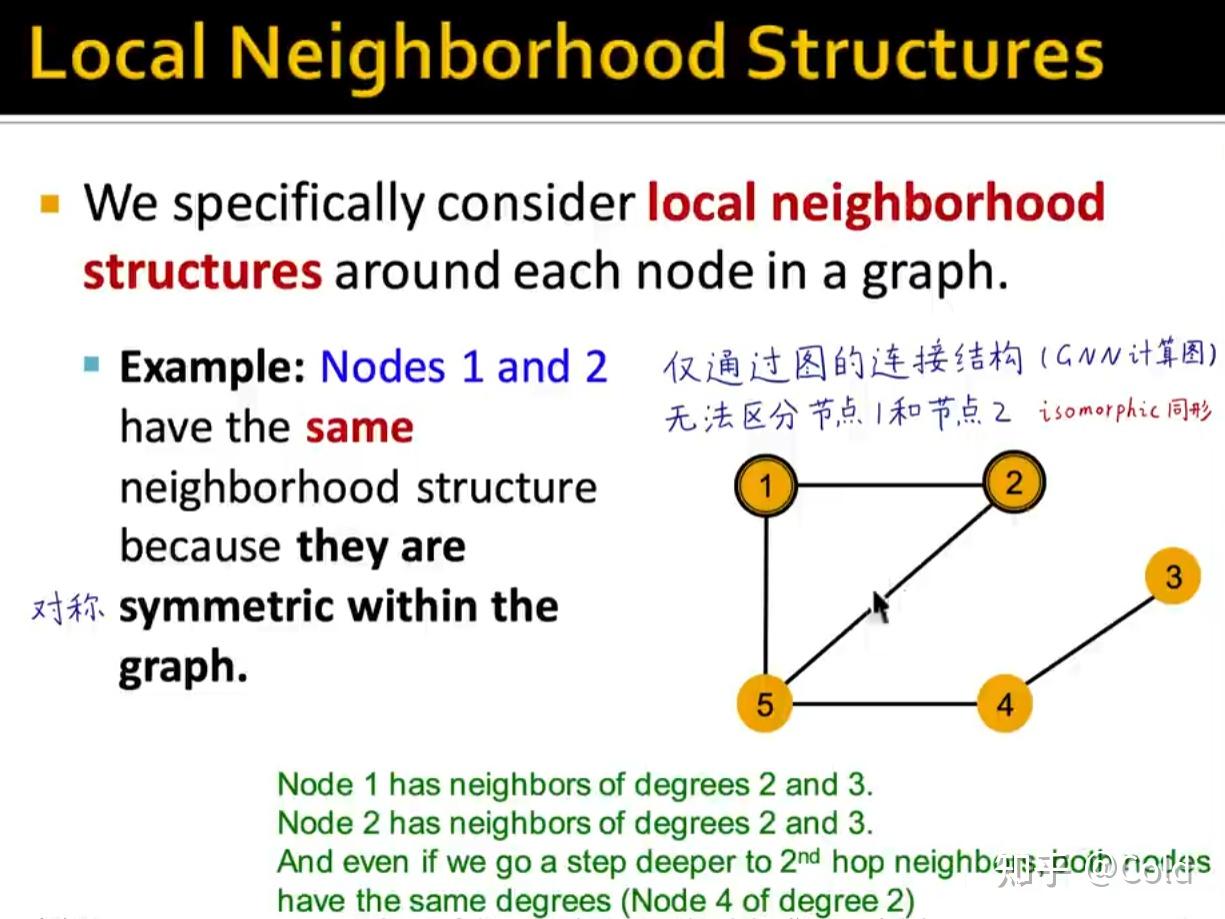
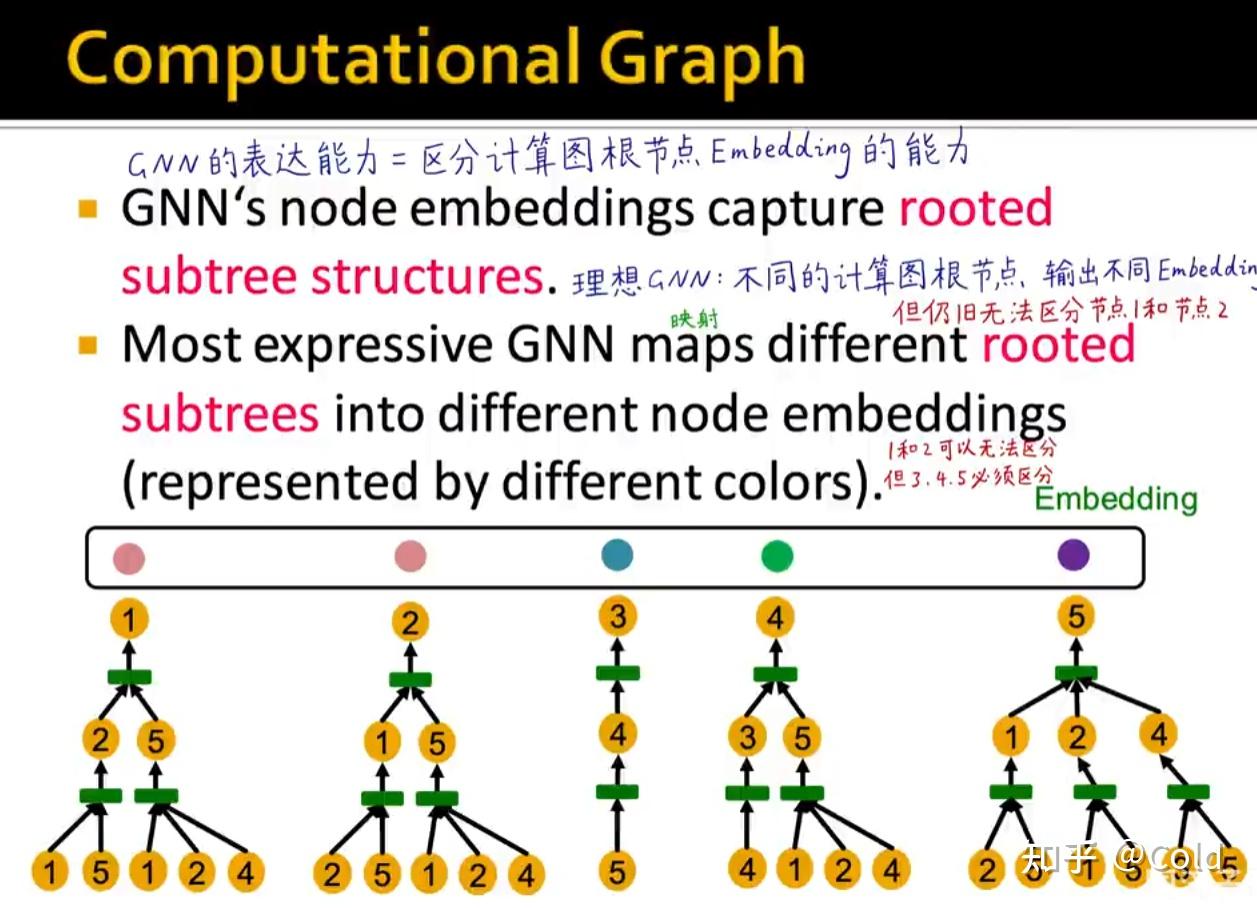
所以总的来说，区分GNN的表示能力的关键在于，不同的节点是否能够学到不同的Embedding，所以GNN的表达能力 = 区分计算图根节点的Embedding的能力

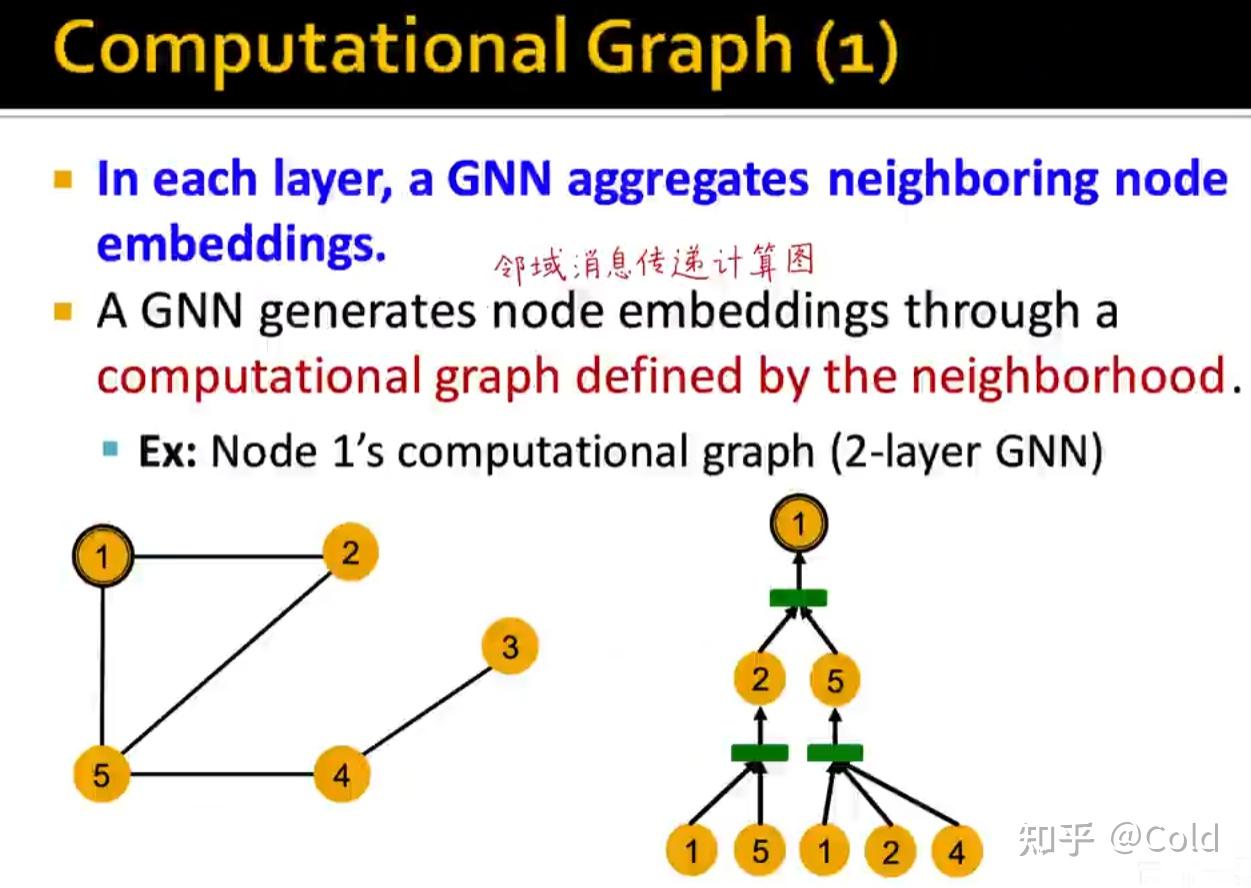
GNN的聚合函数具有顺序不变性，编号这些信息都是无意义的

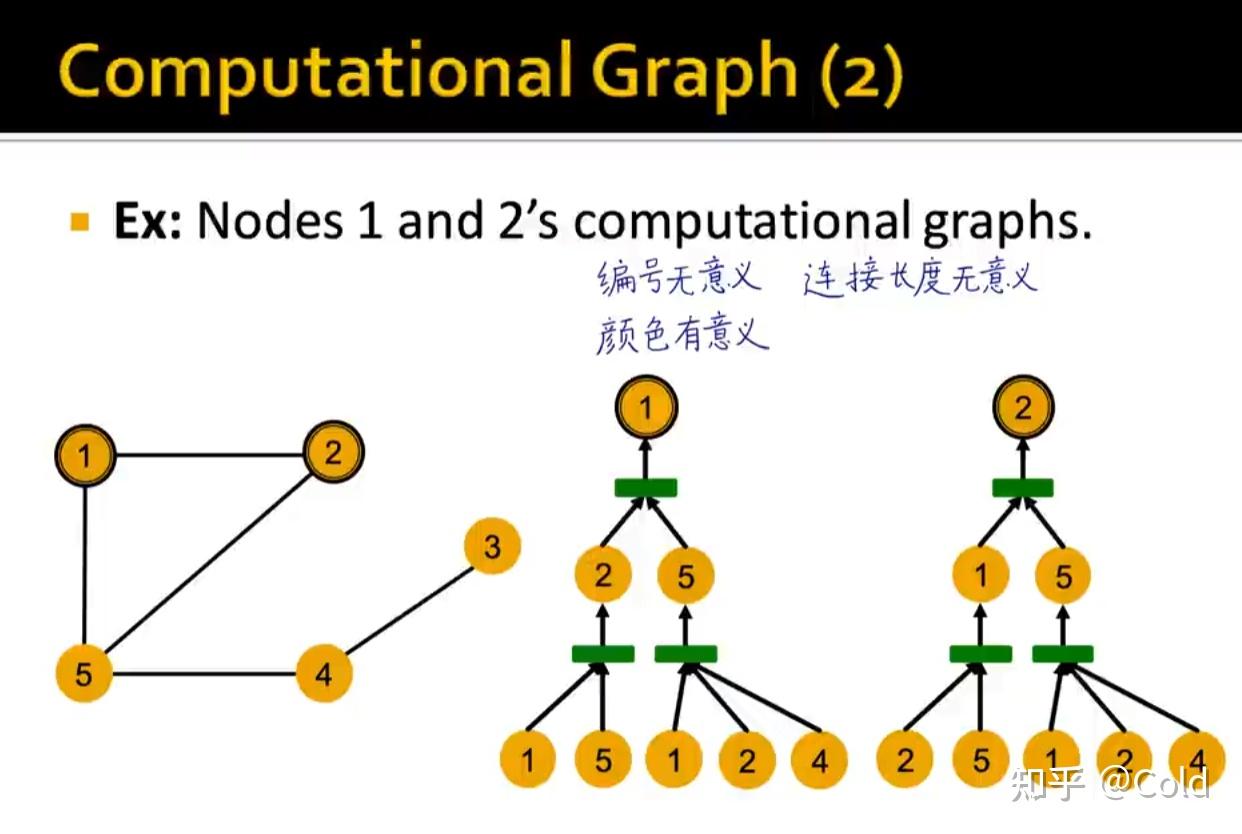
但是基于消息传递机制的GNN，没有办法解决节点一，节点二这样的同形的

你可以无法区分1，2但是一定要可以区分3，4，5

因此为了能够将计算图和Embedding构成映射，这个聚合操作应该是一个单射函数

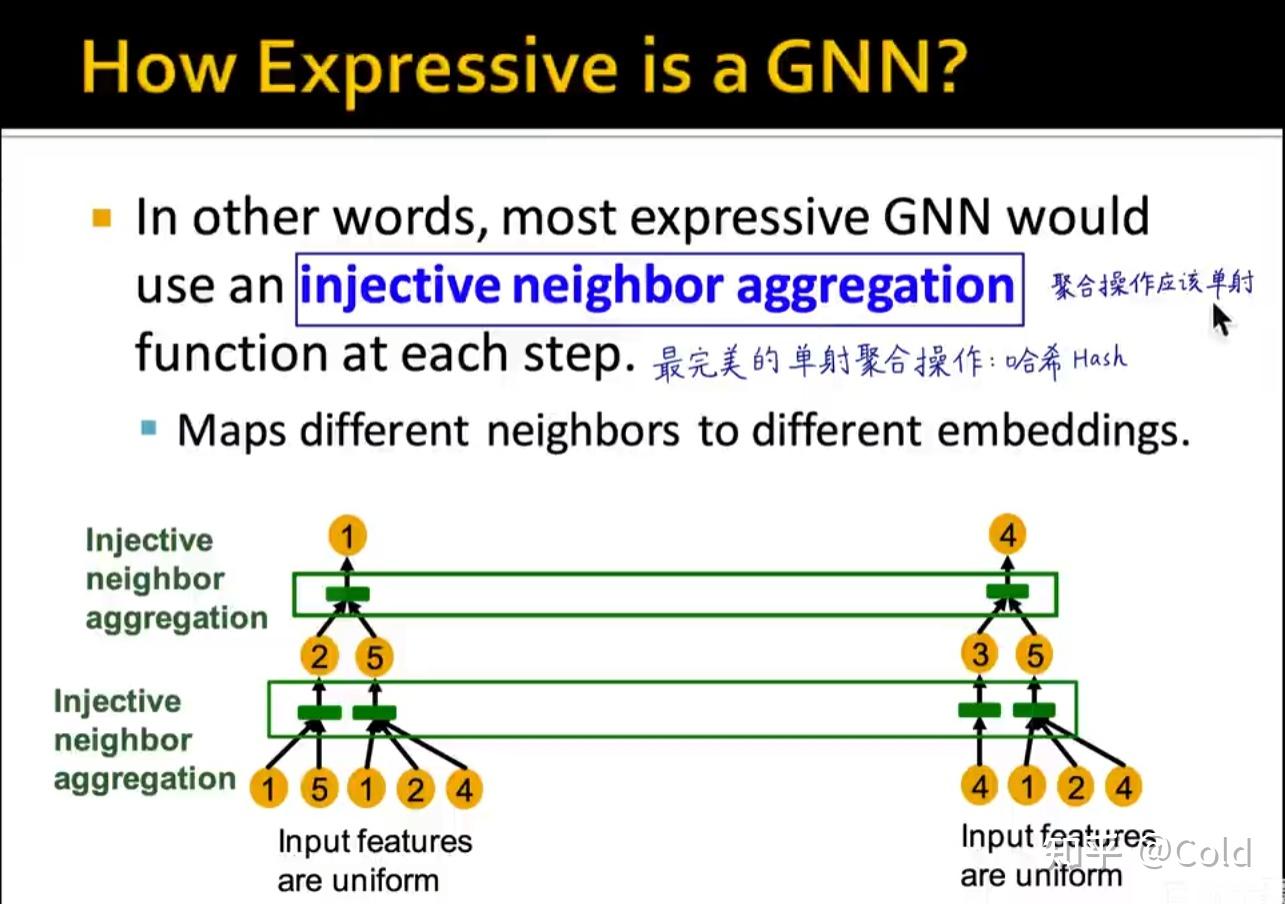
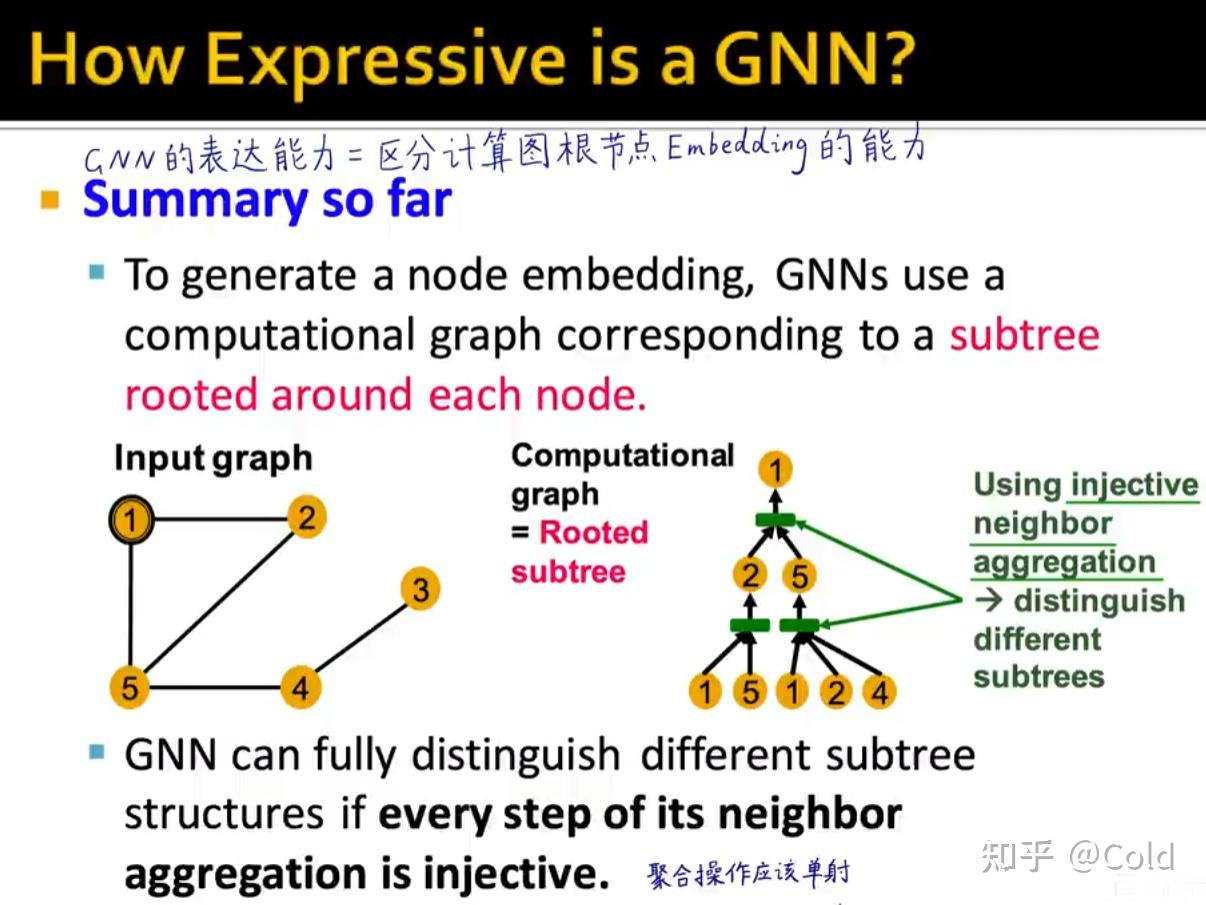
分析常见GNN的表达能力

GCN

GCN的表达能力其实不太强，因为其不是单射。GCN的聚合函数，采用的是平均池化的方式，其并不能保证单射的情况。

由下图我们可以看到，两个不同的向量，却有着相同的输出，这并不能构成单射

GraphSAGE

GraphSAGE采用的是最大池化的方式，那么只要某一维度有一个很大的值，不管其他低的值是什么样的，输出的结果都是一样的。

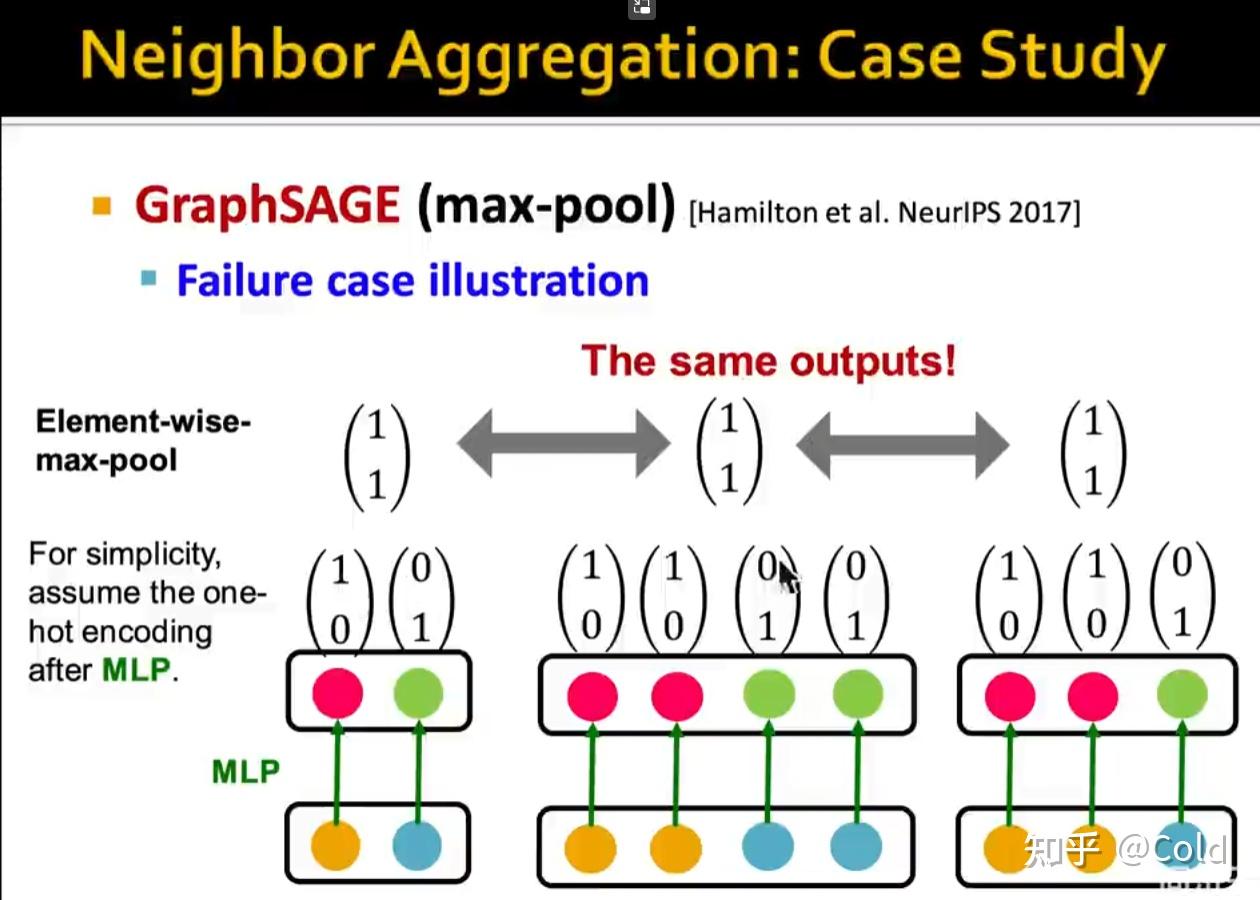
Summary

所以GCN和GraphSAGE的表达能力并不是最强的，他们的聚合函数并不是单射的，所以我们希望设计出一种表达能力最强的神经网络。

所以一个很自然的想法，我们能不能用一个神经网络来拟合出这个单射函数，因为根据万能近似定理，理论上会存在一个聚合函数，使得其表示能力最强。

Graph lsomorphism Network（GIN）

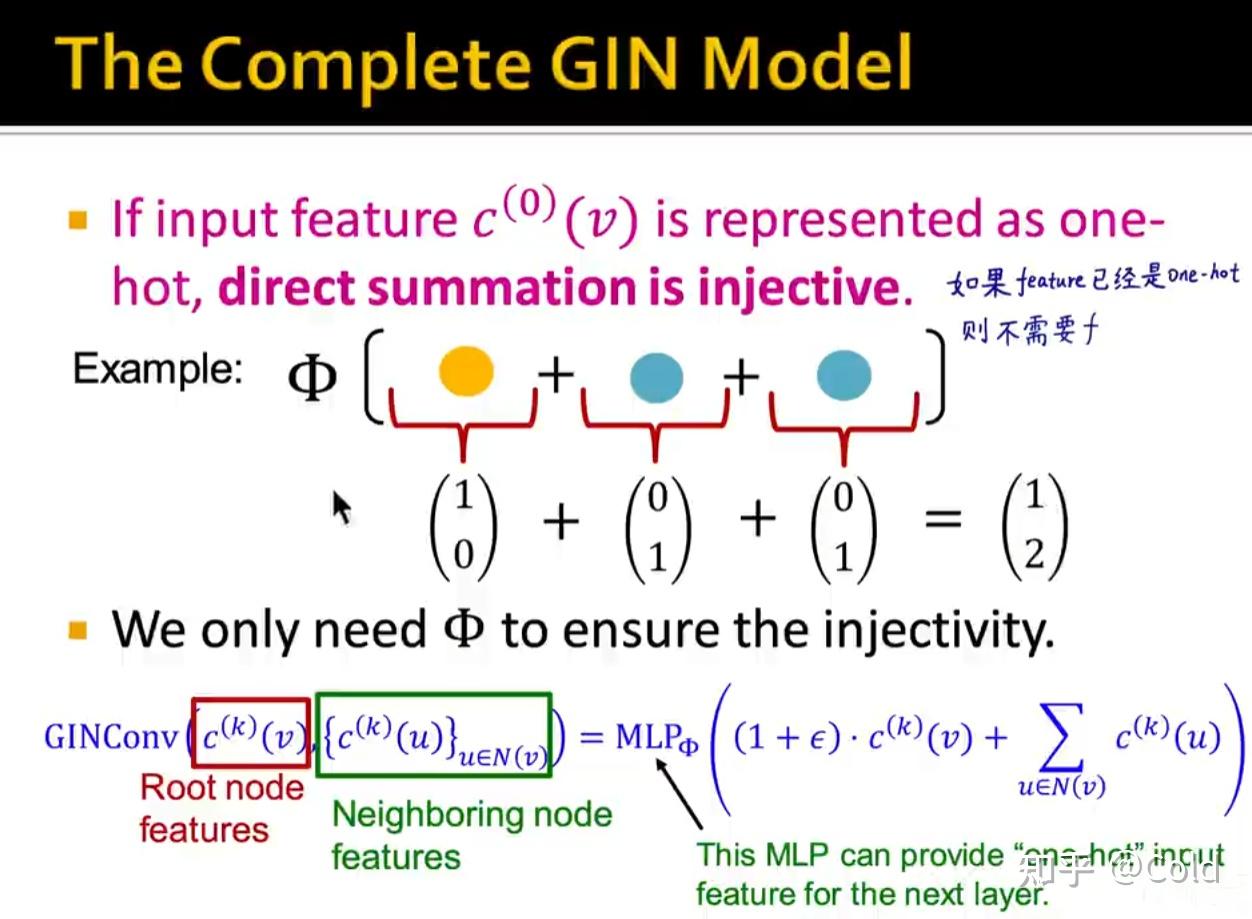
CS224w的主讲人在ICLR2019的论文中提出，任何一个多重集函数都可以被表达成下图中所示的形式。

可以简单的理解为，f用 one-hot 编码，来对“颜色”进行表示，然后求和函数就是对各个“颜色”进行编码，再通过一个单射函数 \Phi 产生新的向量编码。

经验证，训练好的GIN不会存在不同的多重集输出同样的Embedding的结果

如果feature已经是one-hot向量编码的形式了，那么就不需要 f 函数对“颜色”进行编码了，我们只需要 \Phi 对其进行单射即可，当前层的MLP的输出会为下一层的MLP提供“one-hot”向量的输入。

论文细节补充

到此我们已经充分描述GIN模型了，我们可以发现他和传统图机器学习中的WL kernel非常的相似，甚至可以说是神经网络版的WL graph kernel

WL-Kernel

我们先来回顾一下WL kernel的Color Refinement操作，我们将图节点本身的信息，融合连接信息，对颜色进行聚合。

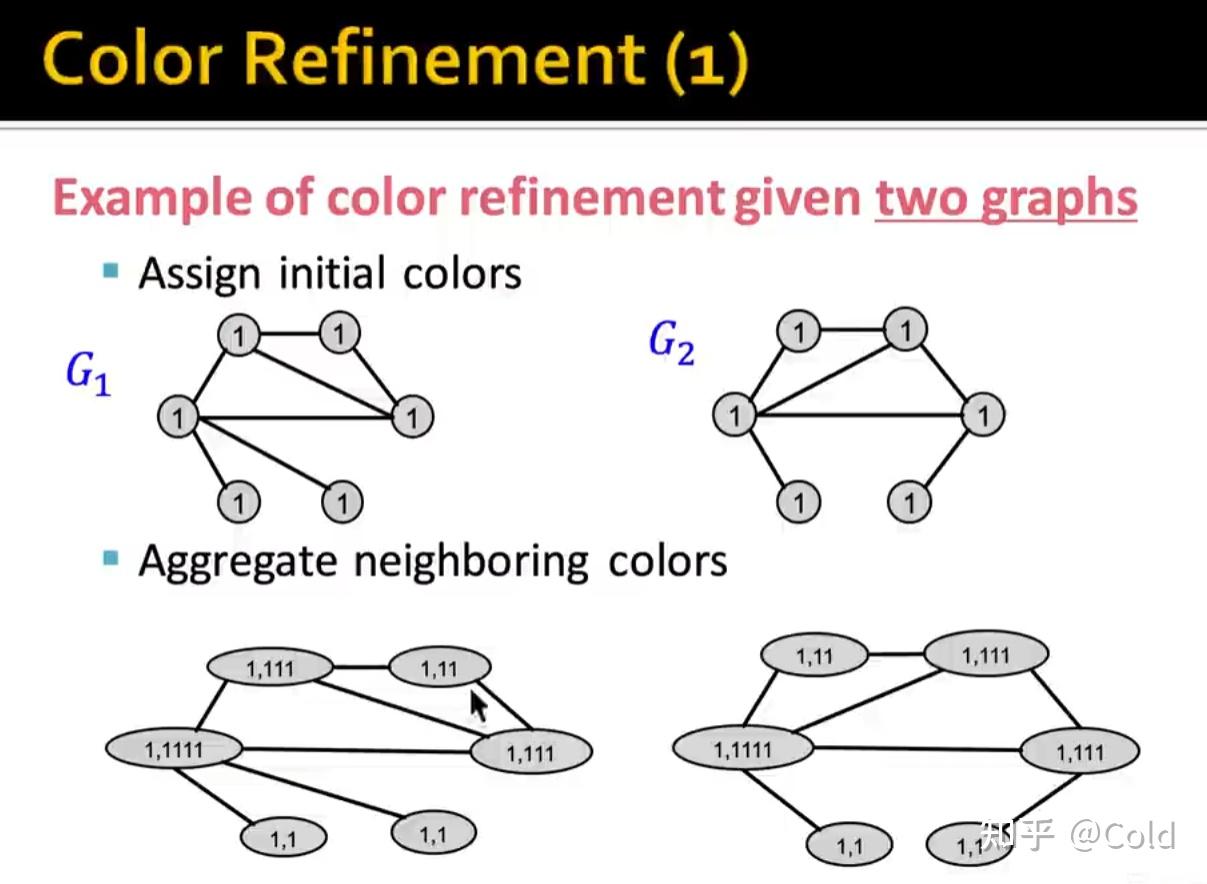
然后对聚合后的值，构建一个Hash table进行映射

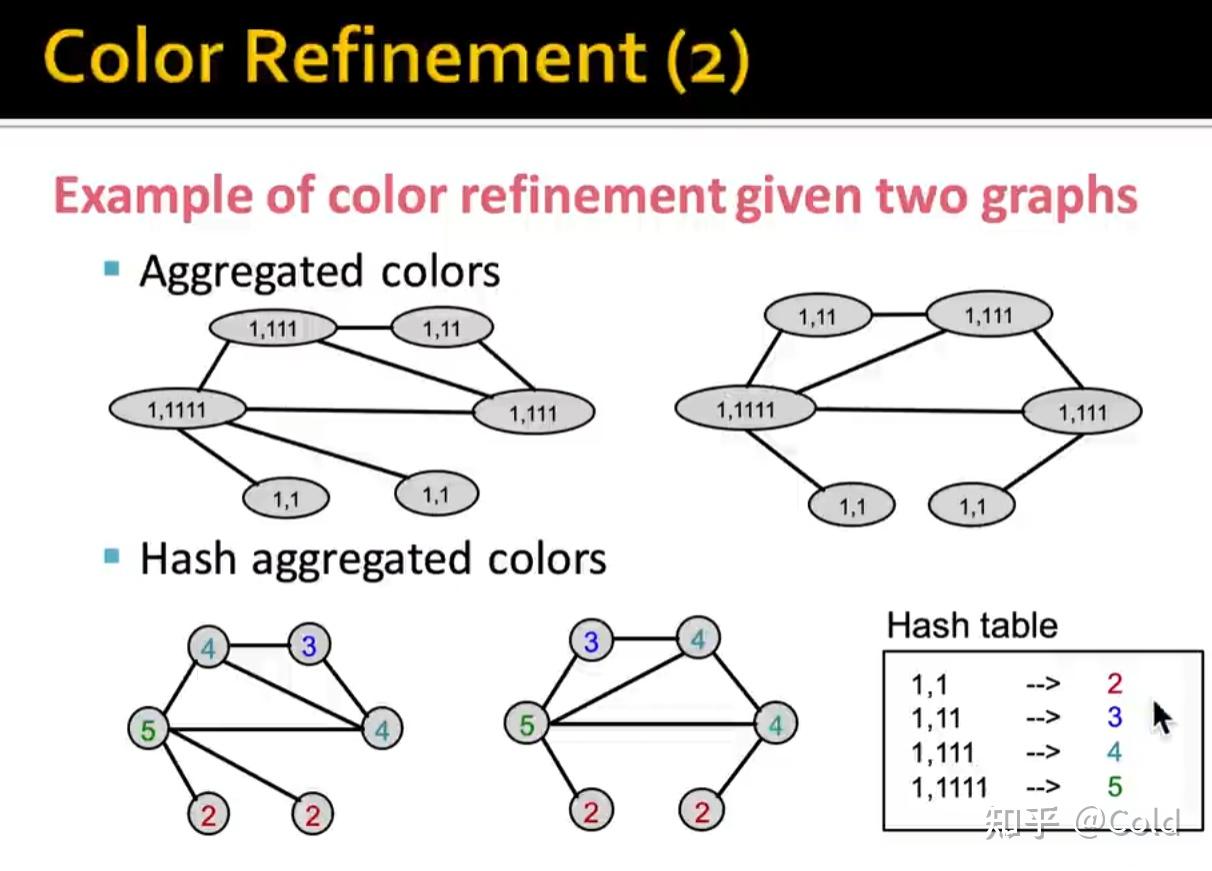
再次对颜色进行聚合

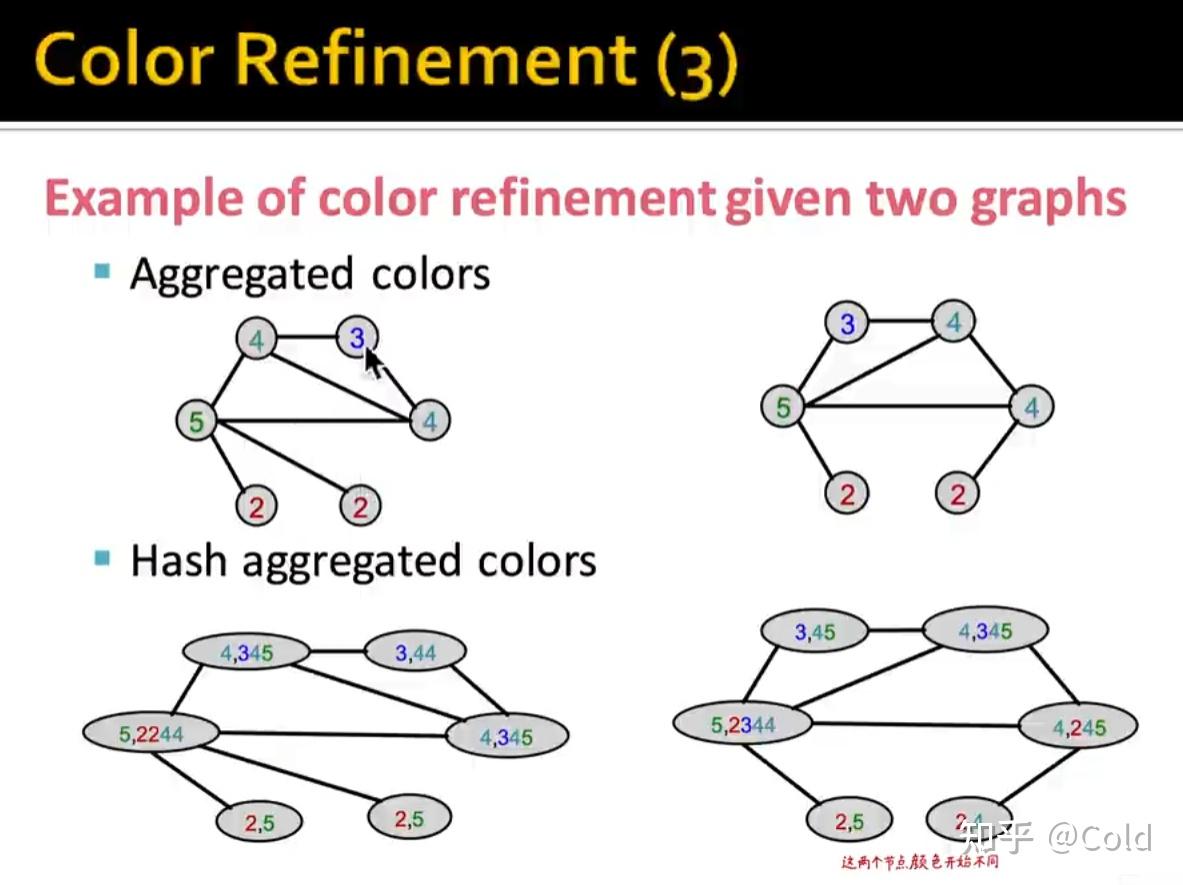
通过多次的迭代以后，我们可以把不同颜色节点的个数写成一个向量，作为全图的向量

所以我们就可以通过WL-kernel的方法，判断两个图是否同形，计算它们的距离，即对两个向量点乘计算余弦相似度。

所以本质上WL-kernel也是一种哈希的方式，将自己的信息和邻居信息聚合后进行映射，迭代了几次的HASH就是计算了K跳内的邻居的信息的HASH

因此GIN和WL-kernel非常的相似， c^{(k)}(v) 和WL-Kernel类似，有几层的GINConv就蕴含着 K 跳邻居范围内的信息。

总的来说 WL Graph Kernel是一个通用的框架，GIN做的Node embedding是低维连续稠密包含语义的向量，因此它可以捕获细粒度的信息。并且可以根据下游任务，进行优化。

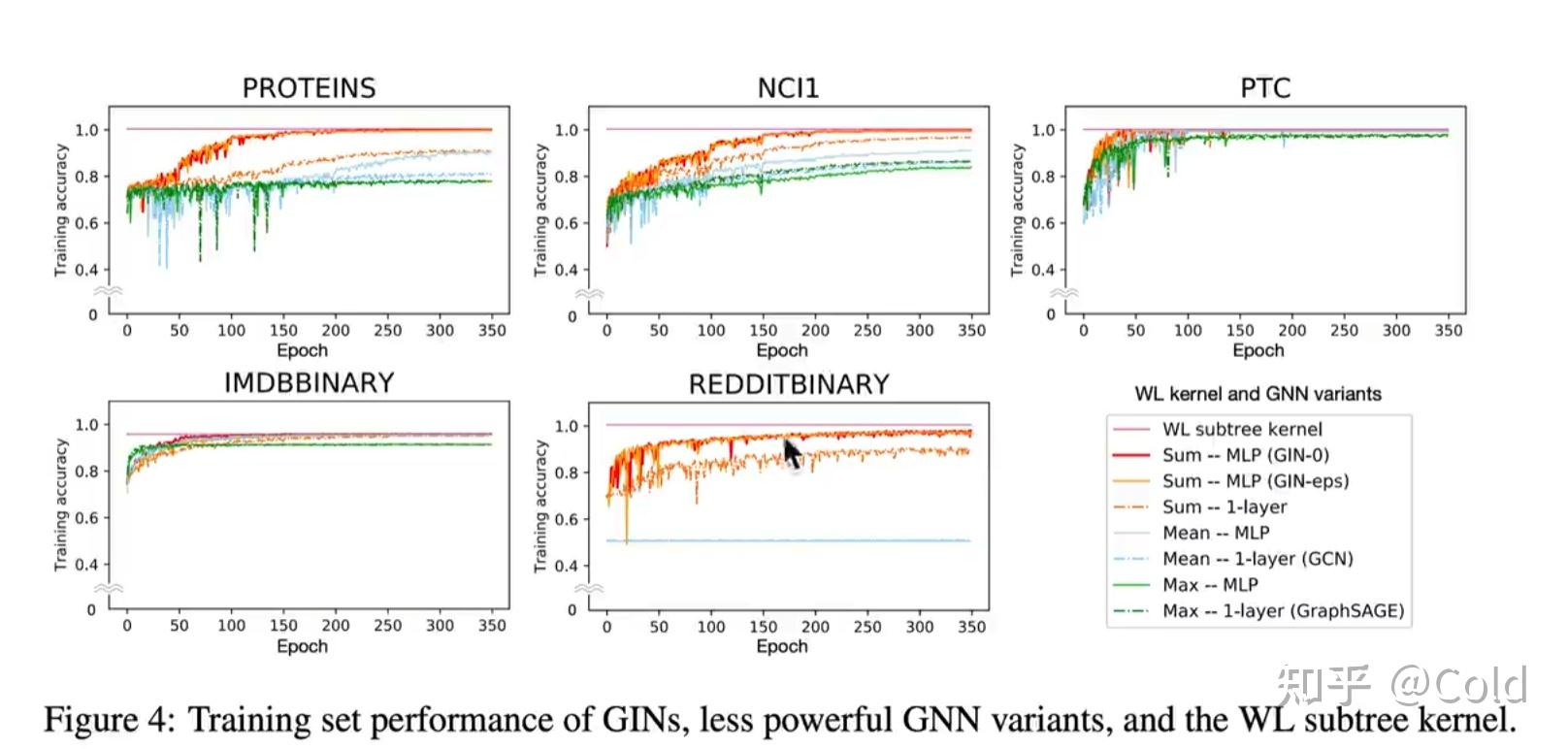
从下图中更加证实了，WL-Kernel是GNN模型表达的上界

GNN 工程调参技巧

Summary

我们这一讲主要衡量的是图表示能力，其中最关键的就是构建一个单射多重集函数，我们用神经网络来拟合这个聚合函数，得到了最具表示能力的模型GIN。然后 GIN 和 WL graph kernel 非常的相似，他们都可以表现出绝大多数的图。