手把手教你43行代码写红黑树（包括删除操作）

Hello world

# a.hs
main = putStrLn "hello world"

运行

$ runghc a.hs
hello world

也有像python一样interactive console

$ ghci
Prelude> putStrLn "hello"
hello

也可以编译成可执行文件

$ ghc a.hs -o a
$ ./a
hello world

List

Prelude> [1,2,3]
[1,2,3]
Prelude> [1..10]
[1,2,3,4,5,6,7,8,9,10]

Haskell的List是单向链表。[1..10]表达式有点像python的range。

head可以获取list的第一个元素，tail函数返回第一个元素之后的list，相当于获得单向链表头节点的value与next

Prelude> head [0..5]
Prelude> tail [0..5]
[1,2,3,4,5]

List Comprehension

Haskell List也有类似Python的List Comprehension。Haskell的语法有点像数学里集合的表示。

 [x | x <- [0..9]]

等同于python里的

[x for x in range(10)]

多层循环也可以

[(x,y) | x <- [0..3], y <- [0..3]]

相当于Python里

[(x,y) for x in range(4) for y in range(4)]

（Haskell也有类似Python中的Tuple）。

也可以加上条件过滤

 [x | x <- [0..9], x `mod` 2 == 1]

相当于Python里

[x for x in range(10) if x % 2 == 1]

"++"运算符可以连接两个list

Prelude> [0..2] ++ [3..5]
[0,1,2,3,4,5]

函数与模式匹配（Pattern Matching)

Haskell函数定义与模式匹配密不可分。

阶乘函数在Haskell中可以这么实现：

fact 0 = 1
fact n = n * (fact (n - 1))

函数调用时，参数不需要用括号括起来。

Prelude> fact 3
6

Haskell调用函数时，按顺序尝试匹配定义中的参数。第一个匹配上的参数对应的定义会被采用。

调用fact 3，匹配fact 0失败（3！=0），匹配fact n成功（n可以匹配任何数），于是返回3 * fact 2。

递归调用fact 2，匹配fact 0失败，匹配fact n成功，返回2 * fact 1。

递归调用fact 1，匹配fact 0失败，匹配fact n成功，返回1 * fact 0。

递归调用fact 0，匹配fact 0成功，返回1。

一路回溯到fact 3，最终返回6。

两行顺序不能颠倒，不然"fact n"将匹配任何参数，而"fact 0"永远不会被匹配到。

Haskell自带大整数支持

Prelude> fact 100
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

类似的方法可以实现斐波那契数列

fib 0 = 0
fib 1 = 1
fib n = fib (n - 1) + fib (n - 2)

读者可能注意到这个斐波那契数列的实现是 O(2^n) 的。下面的方法可以在 O(n) 时间内计算斐波那契数列

helper 0 a _ = a
helper n a b = helper (n - 1) b (a + b)
fib n = helper n 0 1

第一次接触函数编程的读者可以多花一些时间思考一下。

另外对于快速计算斐波那契数列算法感兴趣的读者可以阅读这篇文章。

Immutable

Haskell里数据都是immutable的，创建完就不能修改。这是函数式编程语言的一大特征。如果我要修改List中间一个元素，我只能创建一个新的List；

上面提到的的tail函数没有修改list的内容，只是返回了原list的一部分。

Prelude> let a = [0..3]
Prelude> let b = tail a
Prelude> a
[0,1,2,3]
Prelude> b
[1,2,3]

b中的数据其实是a的一部分。由于haskell不允许list a中的值被修改，所以list b中的值也永远不会变。

":"运算符可以把新的元素加到链表的头部。

Prelude> b
[1,2,3]
Prelude> let c = 0:b
Prelude> c
[0,1,2,3]

注意这里并没有修改b，只是创建了一个新的node，next指针指向list b的head。

如果我往红黑树中插入一个元素，那么就必须创建一个新的红黑树。

但这并不是说红黑树插入一次需要从头到尾 O(n) 创建一个新树。比如，如果新元素插入到左子树，那么右子树没有变化，那么就可以原样保留。可以证明Haskell红黑树的插入删除最终运算复杂度也是 O(logn) 的。

quicksort

有了以上知识，我们已经可以实现一些算法了。

下面是Haskell快速排序算法的实现。

qsort [] = []
qsort (x:xs) = qsort [a | a <- xs, a < x] ++ [x] ++ qsort [a | a <- xs, a >= x]

(x:xs)模式用到了上面提到的":"运算符，可以匹配任何非空List，x是第一个元素，xs是剩下的元素。

别的语言中十几行的算法Haskell只用了两行就可以实现。

当然你可能会说Python也可以写出类似的效果。

在下面红黑树的实现中，结合抽象数据类型（Abstract Data Type）模式匹配(Pattern Matching)将真正发挥威力，而Python将难以做到相同简洁的实现。

抽象数据类型（ADT, Abstract Data Type）

Haskell里复杂数据结构用ADT来定义。

给一个单项列表的例子

data MyList = Empty | MyNode Int MyList deriving (Show)

定义了名为MyList的类型。Empty与MyNode是构造函数，Empty没有参数，MyNode有2个参数，分别是整数和另一个MyNode。

末尾的deriving (Show)是让Haskell自动生成show函数（相当于Java的toString)，方便在interactive console中打印数据的值。

构造一个MyList类型的数据，可以调用其中一个constructor。

Prelude> Empty
Empty
Prelude> MyNode 1 Empty
MyNode 1 Empty
Prelude> MyNode 1 (MyNode 2 Empty)
MyNode 1 (MyNode 2 Empty)

抽象数据类型是函数编程语言特有的功能。如果硬要拿别的语言类比的话，可以把MyList比作Java的interface，Empty与MyNode比作MyList的两个subclasses。

interface MyList {}
class Empty implements MyList {}
class MyNode implements MyList {
  public MyNode(int value, MyList next) {
    this.value = value;
    this.next = next;
  private final int value;
  private final MyList next; 
}

Haskell中也可以像Java的Generic Type一样定义能存储任何类型的MyList

data MyList a = Empty | MyNode a MyList deriving (Show)

这里a是list中value的类型。就好比Java中的T

interface MyList<T> {}
class Empty<T> implements MyList<T> {}
class MyNode<T> implements MyList<T> {
  public MyNode(T value, MyList<T> next) {
    this.value = value;
    this.next = next;
  private final T value;
  private final MyList<T> next; 
}

抽象数据类型也是可以模式匹配的。比如下面的length函数可以用来计算MyList的长度。

length Empty = 0
length MyList _ next = 1 + (length next)

其他有用的语法

fact也可以用if-else来写

fact n = if n == 0 then 1 else n * fact (n - 1)

guard语法相当于一连串的if-else

fib n
  | n == 0 = 0
  | n == 1 = 1
  | otherwise = fib (n - 1) + fib (n - 2)

where与let-in表达式可以定义一些临时变量、函数。

qsort [] = []
qsort (x:xs) =
    left = [a | a <- xs, a < x]
    right = [a | a <- xs, a >= x]
    qsort left ++ [a] ++ qsort right
fib n = helper n 0 1
  where helper 0 a _ = a
        helper n a b = helper (n - 1) b (a + b)

到这里，我们已经了解了实现红黑树需要的所有语法。

由于篇幅限制，很多例子给的很简略，也没有详细的解释。有兴趣学习Haskell的读者可以阅读

红黑树

预警：红黑树的实现需要讨论大量繁琐情况。尽管代码实现只有43行，但理解全部细节依然需要相当的体力。

定义

红黑树是一个平衡二叉搜索树，每个结点(node)非红即黑。

结点的颜色有什么用呢？看完红黑树的定义就清楚了。

1. 红色结点不能相邻（父子）
2. 从根到每一个NIL结点的路径上黑结点的数量相同。

NIL结点就是空子树。叶子的左右结点都是NIL（有的资料中将NIL视为叶子结点。注意本文中的叶子定义有所不同）。

NIL结点视作黑色。

有的资料中要求根为黑，实际上没有必要。

Haskell中红黑树的数据类型定义如下

data RBTree a = Nil | Node Color a (RBTree a) (RBTree a) deriving(Show)
data Color = Red | Black deriving (Show, Eq)

Node的4个参数分别是 颜色，值，左子树，右子树 。

deriving Eq可以让Color数据能够通过==运算符比较。

平衡

由于红色结点不允许相邻，所以从根往叶子走，红色最多就是与黑色交替，如【黑，红，黑，。。。】，红色结点的数量不会超过路径长度的一半。

也就是说，最深的叶子不会比最浅的叶子深一倍。这保证了红黑树一定程度的平衡性。

方便起见，我们把从根到NIL的路径上黑结点的个数叫做黑高(Black Height)。

红黑树中的任意子树都满足红黑树的定义。

如果把根的左右子树看作2个红黑树的话，他们的黑高也是相同的。

有人可能会问，如果所有结点都是黑的，那树不就完全平衡了吗？为什么引入红色结点来把问题变复杂？

没有红色结点的红黑树必定是满的且完全平衡的。在不改变任何结点颜色的前提下，再删除树中任意一个结点都会破坏黑高，树就不再是红黑树了。

红黑树的插入，删除操作通过旋转，重染色的方法确保红黑树的性质不被破坏。

操作

原则上来说只要不破坏红黑树的性质，插入删除时间复杂度 O(logn) ，就都是正确的红黑树实现。

实现方法并不唯一。有的方法代码容易理解，但旋转、染色操作较多；有的算法优化了旋转次数，但讨论情况繁多代码冗长。

仍然有新的红黑树的实现在不断被发现。有兴趣的可以阅读

本文的插入操作基于Okasaki的书里的算法

书中没有给出红黑树的删除算法。删除操作基于Wiki的实现。

插入

我们都知道怎么给一个一般二叉搜索树插入元素：

• 比根小就插入左子树
• 比根大就插入右子树
• 遇到NIL结点时，创建一个新结点取代NIL

红黑树的节点非红即黑。新结点用什么颜色呢？

黑色的话，经过这个结点的路径的黑高就多了1，而红色不影响黑高，所以新结点就用红色。

但是红色新结点的父节点也是红色怎么办？红色结点不就相邻了？

双红矛盾

条件：

父子结点均为红。如果有祖父结点，祖父为黑

目标：

在不破坏黑高的情况下，通过旋转、重染色将红色结点分开

我们枚举所有可能的四种情况来分离相邻的红色结点。每个情况从黑色结点出发遍历两个红色结点的顺序对应了左左，左右，右左，右右四种情况。

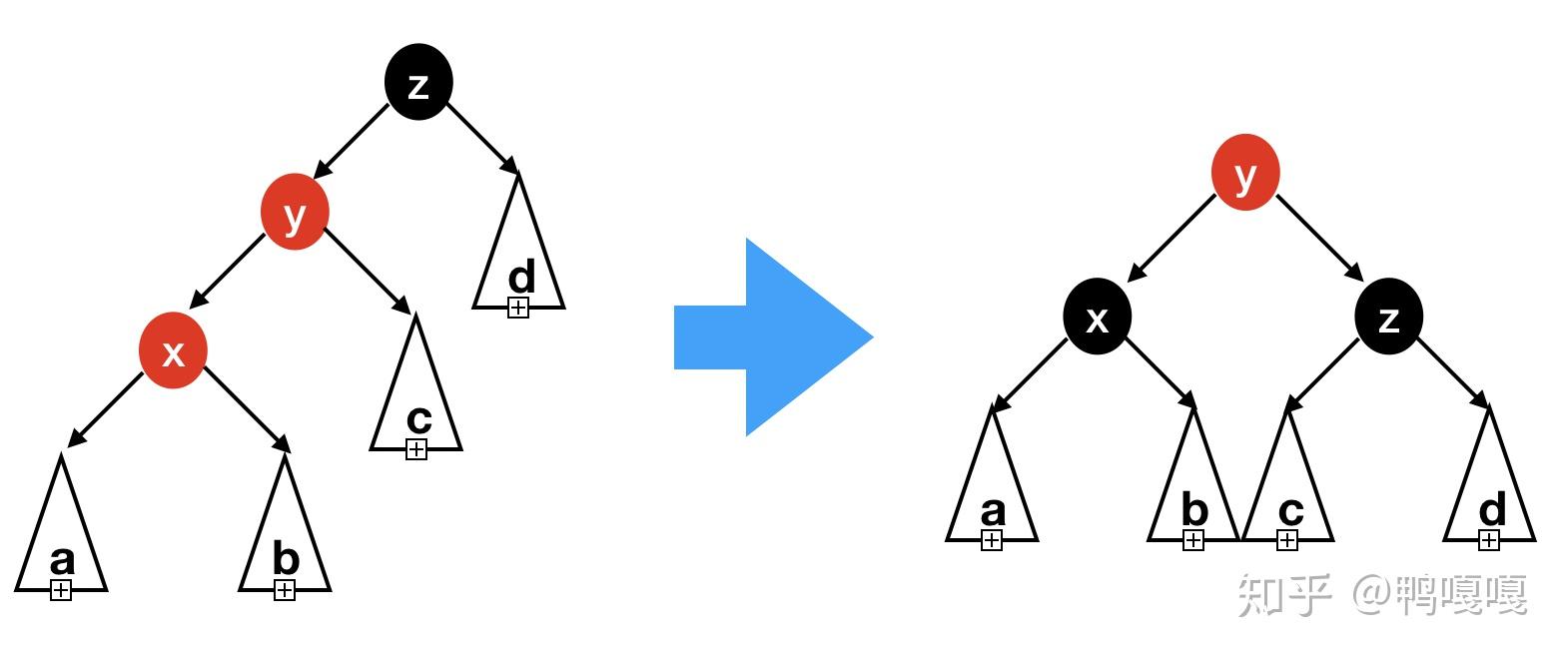
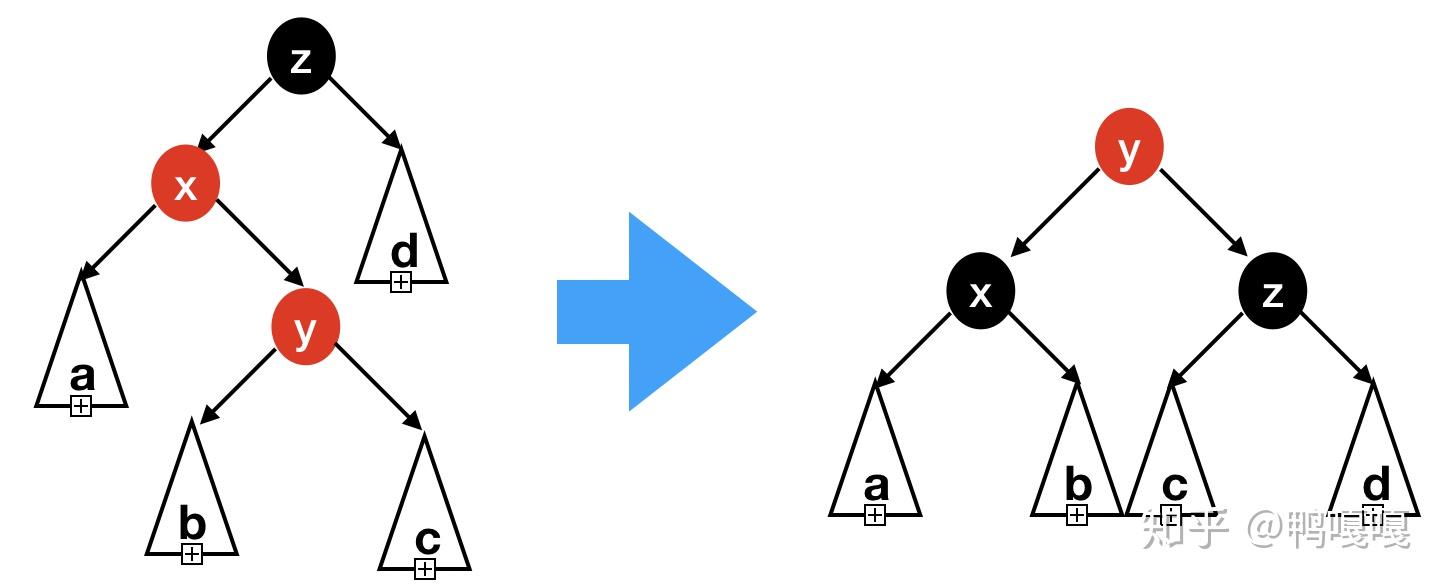
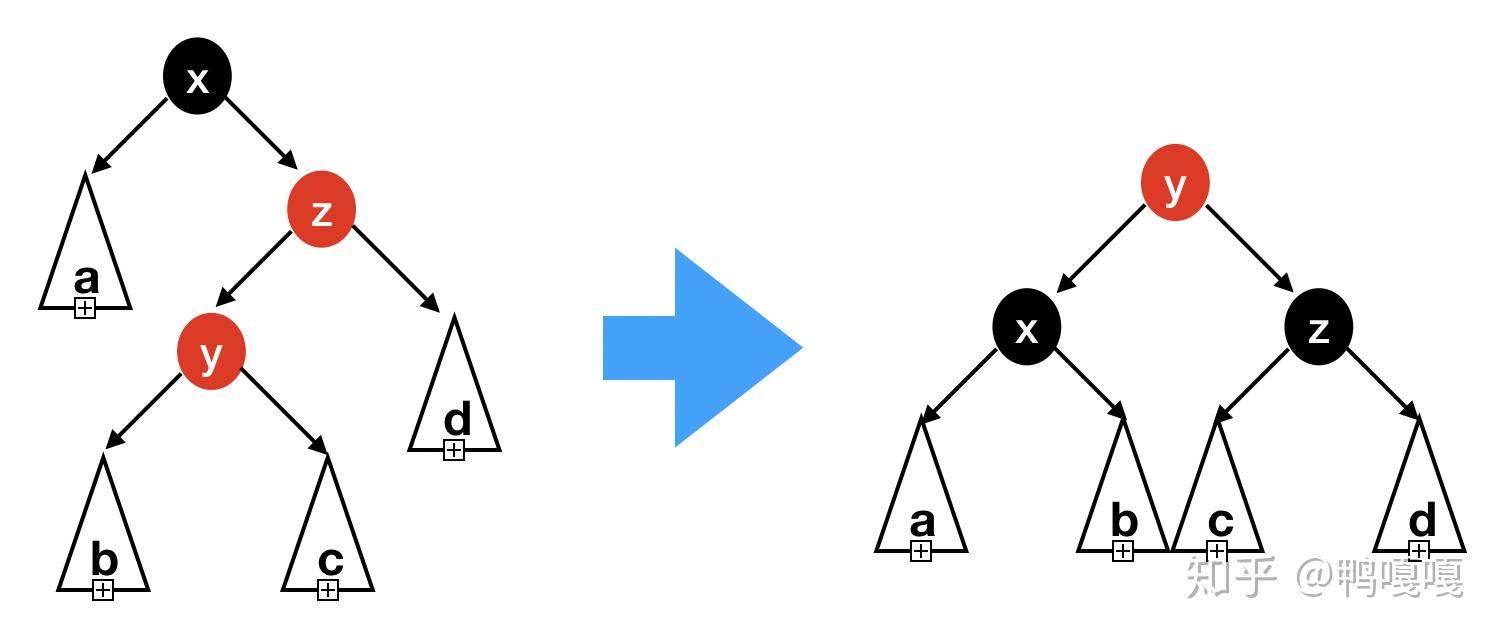
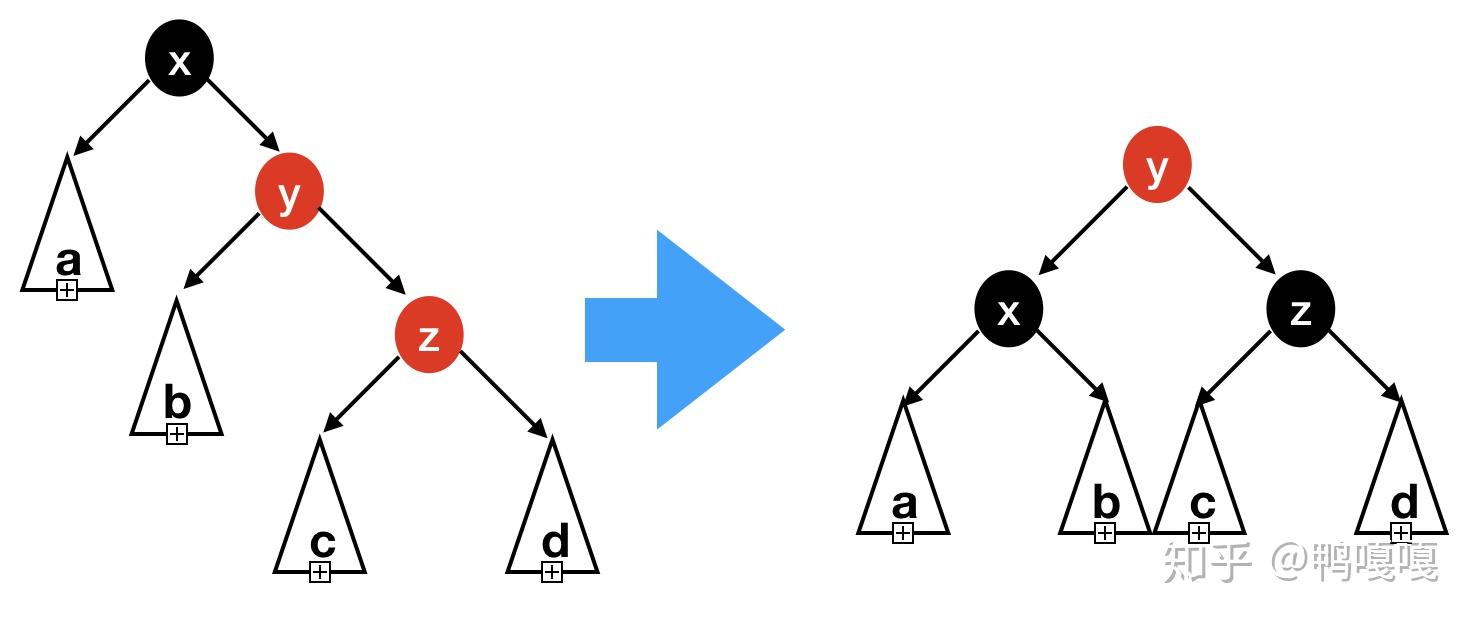
四种情况旋转后的结果是一样的。

注意旋转过后子树的根由黑变红，可能会与上面的祖父节点造成新的双红矛盾，需要进一步解决。

这四种旋转中红色父子结点需要依赖黑色的祖父节点来完成旋转。如果没有祖父结点怎么办呢？

把根变黑就行了。

根由红变黑不破坏红黑树的性质，只不过把整棵树的黑高+1。

C++或者Java要讨论这五种情况通常需要多个指针赋值与颜色变换的操作，代码难写难读。

而Haskell只需要13来行代码。其中复杂的情况讨论只用了5行代码。

blacken Nil = Nil
blacken (Node _ value left right) = Node Black value left right
insert x root = blacken $ insert' root
  where insert' Nil = Node Red x Nil Nil
        insert' root@(Node color y left right) 
            | x < y = balance color y (insert' left) right
            | x > y = balance color y left (insert' right)
            | otherwise = root
balance Black z (Node Red x a (Node Red y b c)) d = Node Red y (Node Black x a b) (Node Black z c d)
balance Black z (Node Red y (Node Red x a b) c) d = Node Red y (Node Black x a b) (Node Black z c d)
balance Black x a (Node Red y b (Node Red z c d)) = Node Red y (Node Black x a b) (Node Black z c d)
balance Black x a (Node Red z (Node Red y b c) d) = Node Red y (Node Black x a b) (Node Black z c d)
balance color value left right = Node color value left right

balance的前四个模式对应了4种情况，第五个模式覆盖了其他没有双红矛盾的情况。

insert函数最后用blacken把根结点无脑染黑，确保潜在的根部双红矛盾得到解决。

删除

红黑树的删除也是基于二分查找树的删除的。

先找到要删的结点N，

1. 如果N是叶子，直接删掉
2. 如果N有一个孩子，把孩子提上来取代N
3. 如果N有两个孩子，把自己根右子树最小结点的值对换，再从右子树中删除最小结点

注意到调换值不改变颜色，不会破坏黑高，第三种情况最终归约到1,2中的一种情况。

如果N只有一个孩子，那么那个孩子一定是红色，否则N左右孩子不平衡，而N一定是黑色结点。这时只要把这个孩子提上来取代N，颜色变黑即可。

如果N没有孩子，N非红即黑。

如果是红色的话，直接删掉即可，不影响整棵树黑高。

真正困难的情况是N为黑色且没有孩子的情况。

删除N使得N的父节点P的两个孩子不平衡了。

为了让P的两个孩子回复平衡，我们不妨来解决一个更通用的矛盾：

黑高矛盾

条件：

结点P的两个左右两个孩子N，S，N为黑（N可能是NIL）。由于N子树中某结点被删除，黑高减少了1。

目标：

在不产生双红矛盾的前提下，通过旋转、重染色，让整棵树黑高平衡。

有人可能要问，谁说N一定有父节点P的？如果N是根，那么直接删除就好，整棵树就变成了NIL。

我们不妨假设N是P的左子树。如果N是右子树，可以用对称的方法解决矛盾。

我们之所以把问题通用化，是因为黑高矛盾在某些情况下没有办法通过局部变换来解决，而需要像插入操作一样，把矛盾转移到别处再解决。

考虑我们之前提过的例子，假想一个满的红黑树全是黑结点。删除任何一个黑色叶子，那必定需要翻天覆地的变化才能保证整棵树黑高平衡。

接下来我们讨论所有黑高矛盾的可能情况。

先按照S的颜色讨论。

情况1： S红。根据红黑树性质，P一定黑，S的两个孩子也为黑。可以通过一次左旋+重染色让N的兄弟变黑，矛盾被转移到S为黑的情况。

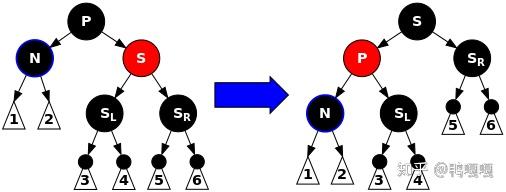
情况2： S黑。根据P的颜色讨论

情况2.1: S黑P红。对调P与S的颜色，这样S子树的黑高少了1，P的两个孩子平衡了。P子树的黑高多了1，补上了左右孩子少掉的黑高。根由红变黑，不用担心出现双红矛盾。完美。

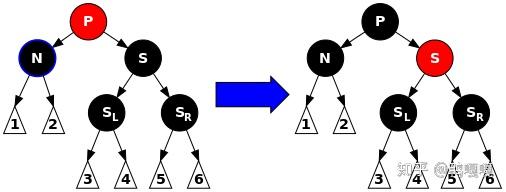
情况2.2: S黑P黑。把S变红，这样S子树黑高少1，N，S就平衡了，但是P的黑高也少了1，祖父结点的两个孩子又不平衡了。新矛盾转交给祖父结点处理。

当然如果P就是根，没有祖父节点，那就不存在新的黑高矛盾。

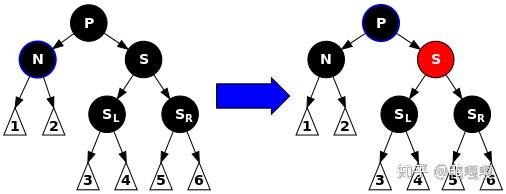
这就结束了吗？

结点颜色可以随意变么？红变黑没问题，黑变红造成双红矛盾怎么办？

设S的左右孩子分别是SL，SR。

上面2.1，2.2仅在SL，SR为黑（NIL也是黑）时适用 。如果SL，SR有红色怎么办呢？

情况2.3 ：SR为红（SL，P的颜色无所谓）

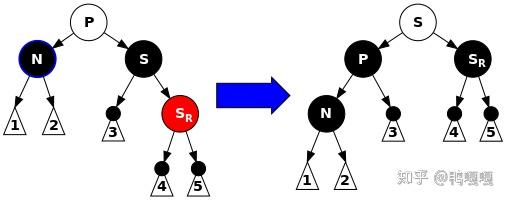
上面的旋转可以把N埋藏到更深一层以弥补N黑高损失，而SR变黑也弥补了SR被拉高造成的黑高损失，最终整体黑高不变。

根的颜色没有发生改变，所以不用担心出现新的双红矛盾。

最后只剩下SL红SR黑这个硬骨头了。

情况2.4 ：SL红，SR黑

S子树中完成下面这个旋转。

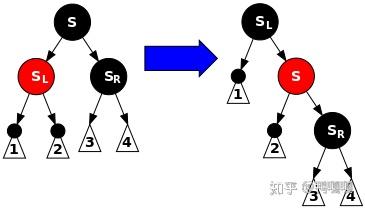
旋转后就变成了 情况2.3

至此，所有情况讨论完毕。

实现如下。

isBlack (Node Red _ _ _) = False
isBlack _ = True
balL color y (left, True) right = (Node color y left right, True)
balL color y (left, False) right = balL' color y left right
balR color y left (right, True) = (Node color y left right, True)
balR color y left (right, False) = balR' color y left right
balL' color1 p n (Node color2 s sl sr)
    | color2 == Red = balL Black s (balL' Red p n sl) sr
    | isBlack sl && isBlack sr = (Node Black p n (Node Red s sl sr), color1 == Red)
    | not (isBlack sr) = (Node color1 s (Node Black p n sl) (blacken sr), True)
    | otherwise = let (Node Red x sll slr) = sl in balL' color1 p n (Node Black x sll (Node Red s slr sr))
balR' color1 p (Node color2 s sl sr) n
    | color2 == Red = balR Black s sl (balR' Red p sr n)
    | isBlack sl && isBlack sr = (Node Black p (Node Red s sl sr) n, color1 == Red)
    | not (isBlack sl) = (Node color1 s (blacken sl) (Node Black p sr n), True)
    | otherwise = let (Node Red x srl srr) = sr in balR' color1 p (Node Black x (Node Red s sl srl) srr) n
delete x t = fst $ delete' x t
  where delete' x Nil = (Nil, True)
        delete' x root@(Node color y left right)
            | x < y = balL color y (delete' x left) right
            | x > y = balR color y left (delete' x right)
            | otherwise = deleteRoot root