GPU加速04:将CUDA应用于金融领域，使用Python Numba加速B-S期权估值模型

PP鲁

我和滴滴云有一些合作，没有GPU的朋友可以前往滴滴云上购买GPU/vGPU/机器学习产品，记得输入AI大师码：1936，可享受9折优惠。GPU产品分时计费，比自己购买硬件更划算，请前往滴滴云官网 http://www. didiyun.com 购买。
很多领域尤其是机器学习场景对GPU计算力高度依赖，所幸一些成熟的软件或框架已经对GPU调用做了封装，使用者无需使用CUDA重写一遍，但仍需要对GPU计算的基本原理有所了解。对于一些无法调用框架的场景，当数据量增大时，非常有必要进行GPU优化。量化金融中经常使用蒙特卡洛模拟和机器学习等技术，是一个非常好的应用GPU并行编程的领域。

本文为英伟达GPU计算加速系列的第四篇，主要基于前三篇文章的内容，以金融领域期权估值案例来进行实战练习。前三篇文章为：

AI时代人人都应该了解的GPU知识：主要介绍了CPU与GPU的区别、GPU架构、CUDA软件栈简介。
超详细Python Cuda零基础入门教程：主要介绍了CUDA核函数，Thread、Block和Grid概念，内存分配，并使用Python Numba进行简单的并行计算。
让Cuda程序如虎添翼的优化技巧：主要从并行度和内存控制两个方向介绍了多流和共享内存两个优化技术。

阅读完以上文章后，相信读者已经对英伟达GPU编程有了初步的认识，这篇文章将谈谈如何将GPU编程应用到实际问题上，并使用Python Numba给出具体的B-S模型实现。

应用场景

我在本系列开篇就曾提到目前GPU的应用场景非常广泛：金融建模、自动驾驶、智能机器人、新材料发现、神经科学、医学影像...不同学科一般都有相应的软件，比如分子动力学模拟软件AMBER 16在英伟达的GPU上的运行速度比仅使用CPU的系统快15倍；金融领域则需要使用GPU加速的机器学习来对各类金融产品做分析和预测。

GPU计算加速使用最广泛的领域要数机器学习和深度学习了。各行各业（包括金融量化）都可以将本领域的问题转化为机器学习问题。幸运的是，一些大神帮我们做了封装，做成了框架供我们直接调用，省去了自己编写机器学习算法的时间，并且对GPU的支持非常强，无论是Google家的TensorFlow，还是Facebook家的PyTorch，以及XGBoost都对英伟达GPU有了非常不错的支持，程序员几乎不需要了解太多CUDA编程技术。虽然机器学习工程师不需要了解编程知识，但还是需要了解一些GPU的基础知识（详见本系列第一篇文章），非常有助于其深度学习项目的落地。关于TensorFlow等框架如何调用GPU，大家可先参考这些框架各自的官方文档。

还有很多问题是与具体场景高度相关的，并不能直接用这些框架和库，需要编程人员针对具体问题来编程。例如量化金融领域常常使用蒙特卡洛模拟，而 CUDA对蒙特卡洛模拟也有非常好的支持 ，当数据量增大时，CUDA的优势非常明显。本文以金融领域著名的Black-Scholes模型为案例来展示如何使用Python Numba进行CUDA并行加速。B-S模型为Numba官方提供的样例程序，我在原来基础上做了一些简单修改。

Black-Scholes模型简介

Black-Scholes模型，简称B-S模型，是一种对金融产品估价的数学模型。该模型由Fischer Black和Myron Scholes提出，后由Robert Merton完善，这几位学者凭借该模型荣获1997年荣获诺贝尔经济学奖。金融主要是在研究现在的钱与未来的钱的价值问题，B-S模型就是一种对期权产品初始价格和交割价格估值的方法。模型的公式如下。

使用上面这个公式，给定期权现价S、交割价格K，期权时间t，可以计算出看涨期权（Call Option）和看跌期权（Put Option）的价格。我本人并不是金融科班出身，就不在此班门弄斧解释这个模型的金融含义了。对于程序员来说，一个重要的能力就是不需要对业务有太深入理解，也能使用代码实现需求。

B-S模型的Python实现

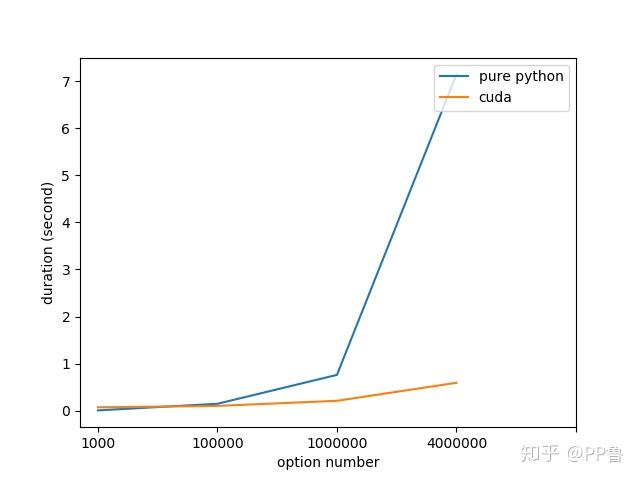
这里我随机生成了一组数据，包括期权现价S、交割价格K和期权时间t，数据维度分别为1000、100000, 1000000, 4000000。分别用"Python + Numpy"和"CUDA"方式实现，在高性能的Intel E5-2690 v4 CPU和Telsa V100 PCI-E版上运行，耗时如下图所示。数据量越小，Python和Numpy在CPU上运行的程序越有优势，随着数据量增大，CPU程序耗时急速上升，GPU并行计算的优势凸显。当数据量为400万时，CUDA程序可以获得30+倍速度提升！试想，如果一个程序之前需要在CPU上跑一天，改成CUDA并行计算后，可能只需要一个小时，这是何等程度的生产力提升啊！

在实现B-S模型时，编写了一个正态分布的累计概率分布函数（Cumulative Distribution Function）： cnd 。关于概率密度函数和累计概率分布函数我这里不做赘述，本科的概率论课程都会涉及，网络上也有很多详细介绍。我随机初始化了一些数据，并保存在了numpy向量中。注意，在CPU上使用numpy时，尽量不要用 for 对数组中每个数据处理，而要使用numpy的向量化函数。对于CPU程序来说， numpy向量 尽量使用 numpy.log() 、 numpy.sqrt() 、 numpy.where() 等函数，因为numpy在CPU上做了大量针对向量的计算优化。但是对于标量，numpy可能比math库慢。还需要注意的是， Numba的CUDA有可能不支持部分numpy向量操作 。其他CPU的Python加速技巧，我会在后续文章中分享。

Python Numba库支持的Numpy特性： https:// numba.pydata.org/numba- doc/dev/reference/numpysupported.html

整个程序如下：

import numpy as np
import math
from time import time
from numba import cuda
from numba import jit
import matplotlib
# 使用无显示器的服务器进行计算时，需加上下面这行，否则matplot报错
matplotlib.use('Agg')
import matplotlib.pyplot as plt
def timeit(func ,number_of_iterations, input_args):
    # 计时函数
    start = time()
    for i in range(number_of_iterations):
        func(*input_args)
    stop = time()
    return stop - start
def randfloat(rand_var, low, high):
    # 随机函数
    return (1.0 - rand_var) * low + rand_var * high
RISKFREE = 0.02
VOLATILITY = 0.30
def cnd(d):
    # 正态分布累计概率分布函数
    A1 = 0.31938153
    A2 = -0.356563782
    A3 = 1.781477937
    A4 = -1.821255978
    A5 = 1.330274429
    RSQRT2PI = 0.39894228040143267793994605993438
    K = 1.0 / (1.0 + 0.2316419 * np.abs(d))
    ret_val = (RSQRT2PI * np.exp(-0.5 * d * d) *
               (K * (A1 + K * (A2 + K * (A3 + K * (A4 + K * A5))))))
    return np.where(d > 0, 1.0 - ret_val, ret_val)
    # 上面的Numpy函数比下面使用循环效率高很多
    # for i in range(len(d)):
    #     if d[i] > 0:
    #         ret_val[i] = 1.0 - ret_val[i]
    # return ret_val
def black_scholes(stockPrice, optionStrike, optionYears, riskFree, volatility):
    # Python + Numpy 实现B-S模型
    S = stockPrice
    K = optionStrike
    T = optionYears
    r = riskFree
    V = volatility
    sqrtT = np.sqrt(T)
    d1 = (np.log(S / K) + (r + 0.5 * V * V) * T) / (V * sqrtT)
    d2 = d1 - V * sqrtT
    cndd1 = cnd(d1)
    cndd2 = cnd(d2)
    expRT = np.exp(- r * T)
    callResult = S * cndd1 - K * expRT * cndd2
    putResult = K * expRT * (1.0 - cndd2) - S * (1.0 - cndd1)
    return callResult, putResult
@cuda.jit(device=True)
def cnd_cuda(d):
    # 正态分布累计概率分布函数
    # CUDA设备端函数
    A1 = 0.31938153
    A2 = -0.356563782
    A3 = 1.781477937
    A4 = -1.821255978
    A5 = 1.330274429
    RSQRT2PI = 0.39894228040143267793994605993438
    K = 1.0 / (1.0 + 0.2316419 * math.fabs(d))
    ret_val = (RSQRT2PI * math.exp(-0.5 * d * d) *
               (K * (A1 + K * (A2 + K * (A3 + K * (A4 + K * A5))))))
    if d > 0:
        ret_val = 1.0 - ret_val
    return ret_val
@cuda.jit
def black_scholes_cuda_kernel(callResult, putResult, S, K,
                       T, r, V):
    i = cuda.threadIdx.x + cuda.blockIdx.x * cuda.blockDim.x
    if i >= S.shape[0]:
        return
    sqrtT = math.sqrt(T[i])
    d1 = (math.log(S[i] / K[i]) + (r + 0.5 * V * V) * T[i]) / (V * sqrtT)
    d2 = d1 - V * sqrtT
    cndd1 = cnd_cuda(d1)
    cndd2 = cnd_cuda(d2)
    expRT = math.exp((-1. * r) * T[i])
    callResult[i] = (S[i] * cndd1 - K[i] * expRT * cndd2)
    putResult[i] = (K[i] * expRT * (1.0 - cndd2) - S[i] * (1.0 - cndd1))
def black_scholes_cuda(stockPrice, optionStrike,
                        optionYears, riskFree, volatility):
    # CUDA实现B-S模型
    blockdim = 1024
    griddim = int(math.ceil(float(len(stockPrice))/blockdim))
    device_callResult = cuda.device_array_like(stockPrice)
    device_putResult = cuda.device_array_like(stockPrice)
    device_stockPrice = cuda.to_device(stockPrice)
    device_optionStrike = cuda.to_device(optionStrike)
    device_optionYears = cuda.to_device(optionYears)
    black_scholes_cuda_kernel[griddim, blockdim](
            device_callResult, device_putResult, device_stockPrice, device_optionStrike,
            device_optionYears, riskFree, volatility)
    callResult = device_callResult.copy_to_host()
    putResult= device_putResult.copy_to_host()
    cuda.synchronize()
    return callResult, putResult
def main():
    pure_time_list = []
    cuda_time_list = []
    dtype = np.float32
    data_size = [10, 1000, 100000, 1000000, 4000000]
    for OPT_N in data_size:
        print("data size :" + str(OPT_N))
        stockPrice = randfloat(np.random.random(OPT_N), 5.0, 30.0).astype(dtype)
        optionStrike = randfloat(np.random.random(OPT_N), 1.0, 100.0).astype(dtype)
        optionYears = randfloat(np.random.random(OPT_N), 0.25, 10.0).astype(dtype)
        input_args=(stockPrice, optionStrike, optionYears, RISKFREE, VOLATILITY)
        pure_duration = timeit(black_scholes, 20, input_args)
        pure_time_list.append(pure_duration)
        cuda_duration = timeit(black_scholes_cuda, 20, input_args)
        cuda_time_list.append(cuda_duration)
    print(pure_time_list)
    print(cuda_time_list)
    plt.plot(pure_time_list[1:], label='pure python')
    plt.plot(cuda_time_list[1:], label='cuda')
    plt.legend(loc='upper right')
    plt.xticks(np.arange(5), ('1000', '100000', '1000000', '4000000'))
    #设置坐标轴名称
    plt.ylabel('duration (second)')