时间序列单位根检验步骤详解
本文章的单位根检验指的是最常见的DF、ADF和PP单位根检验。
什么是单位根检验
p阶AR模型 y_t=\alpha+\phi_1y_{t-1}+\phi_2y_{t-2}+...+\phi_py_{t-p}+\omega_t , \omega_t 是白噪声, \Rightarrow y_t-\phi_1y_{t-1}+\phi_2y_{t-2}+...+\phi_py_{t-p}=\alpha+\omega_t \Rightarrow (1-\phi_1L+\phi_2L^2+...+\phi_pL^p)y_t=\alpha+\omega_t ,L是延迟算子。自回归滞后系数多项式令其为零得方程 1-\phi_1L+\phi_2L^2+...+\phi_pL^p=0 ,此处把L看成是普通的未知变量。此方程即为自回归滞后系数特征方程,如果该方程存在为1的根(即存在L=1的情况),则称方程存在单位根。比如“随机游走”过程的模型是 y_t=y_{t-1}+\omega_t ,特征方程是 1-L=0 ,解为 L=1,所以随机游走是一个 单位根过程 。单位根检验就是在检验序列是否是“单位根过程(非平稳序列)”,即特征方程存在为1的根,否则就是平稳过程。“发散过程(特征方程存在根的绝对值大于1)”并不是我们研究的对象(意思是我们要研究的时间序列都不是发散序列),所以不考虑发散过程。
单位根检验的前提
检验单位根的零假设是:序列是随机游走或者带漂移的随机游走,备择假设是:过程是平稳或者趋势平稳。意味着被检验序列要么平稳,要么包含一个单位根或者趋势平稳。如果包含多个单位根,必须先进行差分到只剩一个单位根,否则检验无效。 单位根检验的统计量分布都是基于假设序列只包含一个单位根 (序列是随机游走或者带漂移的随机游走)。这一点在教科书上没有明文说明,而是隐含的,如果对单位根检验研究的足够多是可以看出这个隐含前提的,但是我估计大部分小白并不能看出这个前提,所以特在此说明。
DF单位根检验的生成过程和检验模型
实际序列是如下两种单位根过程(生成过程):
A,随机游走: y_t=y_{t-1}+\omega_t ; \omega_t 是白噪声;
B,带漂移的随机游走: y_t=\alpha+y_{t-1}+\omega_t,\alpha\ne0 。
为了检验以上两种情况,一共有3种检验模型。
模型1: y_t=\rho y_{t-1}+\omega_t
模型2: y_t=\alpha+\rho y_{t-1}+\omega_t
模型3: y_t=\alpha+\delta t+\rho y_{t-1}+\omega_t
检验如果不能拒绝 \rho=1 ,则接受零假设(序列包含一个单位根),否则拒绝零假设,即序列是平稳或趋势平稳(模型3中的 \delta\ne0 )的。
模型1只能检验过程A,模型2可以检验A,B,模型3可以检验A,B。实际检验的时候到底用哪个检验模型要看零假设和备择假设,所以这就是为什么会有模型2和3两个检验模型去检验同一个零假设的原因。
还有3个联合假设的F检验:
\phi_1:\alpha=0,\rho=1 (针对模型2的零假设)
\phi_2:\alpha=0,\rho=1,\delta=0 (针对模型3)
\phi_3:\rho=1,\delta=0 (针对模型3)
正规检验步骤
- 从模型3开始。 \rho=1 被拒绝,则序列不包含单位根,检验结束(当然了,可以进一步去检验是否是趋势平稳还是只是平稳)。如果不拒绝零假设,则进行F检验 \phi_3 ,如果前面说的前提条件满足,该检验是不能被拒绝的,否则要检查前提条件是否满足或者进一步排查原因。如果 \phi_3 不能拒绝,则必须进一步检验 \phi_2 ,因为我们要进一步确认序列是A和B中的哪一种。如果 \phi_2 被拒绝,则序列是带漂移的随机游走,检验结束。如果 \phi_2 不能被拒绝,意味着序列是随机游走,如果是随机游走,模型2的功效要大于模型3,因为功效低,模型3可能犯二类错接受了错误零假设,所以我们必须用模型2去做进一步的检验。
- 使用模型2,注意了,此处使用模型2的零假设是:序列是随机游走。检验统计量的分布都是基于这个零假设。如果 \rho=1 被拒绝,则序列不包含单位根,序列是平稳的,检验结束。如果不拒绝零假设,则进行F检验 \phi_1 ,不出意外 \phi_1 不能被拒绝,如果拒绝了要排查原因。如果 \phi_1 不能被拒绝,序列有非零均值,则检验结束,序列有零均值,则使用模型1做进一步的检验,因为模型1功效大于模型2。
- 使用模型1,零假设是:序列是随机游走。零假设被拒绝,则序列不包含单位根,检验结束,否则序列是一个随机游走序列。
虽然模型2可以检验生成过程B,但是实际中我们只用它检验A。A和B,模型2的统计量分布是不同的,统计软件中使用模型2做的检验,其零假设都是:过程是随机游走。这一点,切记。对于模型3,在对应的零假设下,A和B这两个过程,其检验统计量分布是一样的。模型3,如果实际过程是存在单位根,并且线性确定性部分 \delta 不为零,则统计量的分布和 \delta 为零的分布不同(如果检验前提满足,则这种情况不会出现)。不同零假设A或B对应不同模型统计量分布可以参考 Hamilton的《时间序列分析》。
ADF检验的步骤和DF检验步骤相同。PP检验过程也是 差不多的。 PP检验的联合F检验在此不做叙述,可以参考 中国人民大学出版社 出版的《现代时间序列分析导论》,我看的是该书第二版。
非常遗憾的一件事情是:常用统计软件不提供联合F检验,只能靠我们手动自行建立模型去做F检验。如何手工进行F检验可以参考 沃尔特·恩德斯的《应用计量经济学:时间序列分析》。
正规步骤的简化
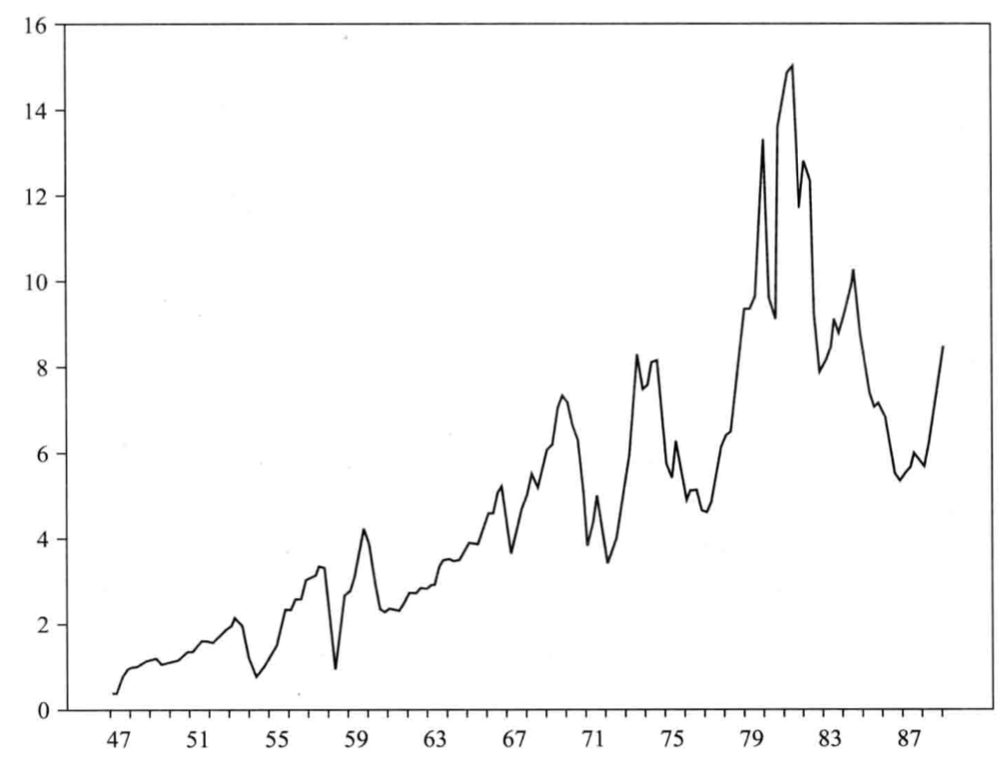
图1序列图显示序列开始上升,然后下降,此序列要么平稳,要么是一个随机游走,所以零假设自然是:序列是随机游走。此时可以使用模型2来开始检验(从正规步骤的步骤2开始)。如果序列是平稳的,显然均值不为零,为了和备择假设对应,所以用模型2开始检验。图中显示序列均值并不为零,所以步骤1是不必要的,可以不做。使用模型1的原因是模型1比模型2功效更高,为了避免犯二类错误才进一步进行模型1的检验,如果模型2不能拒绝零假设,而序列均值非零,模型1检验结果不可能会拒绝零假设,所以模型1的检验没有必要。
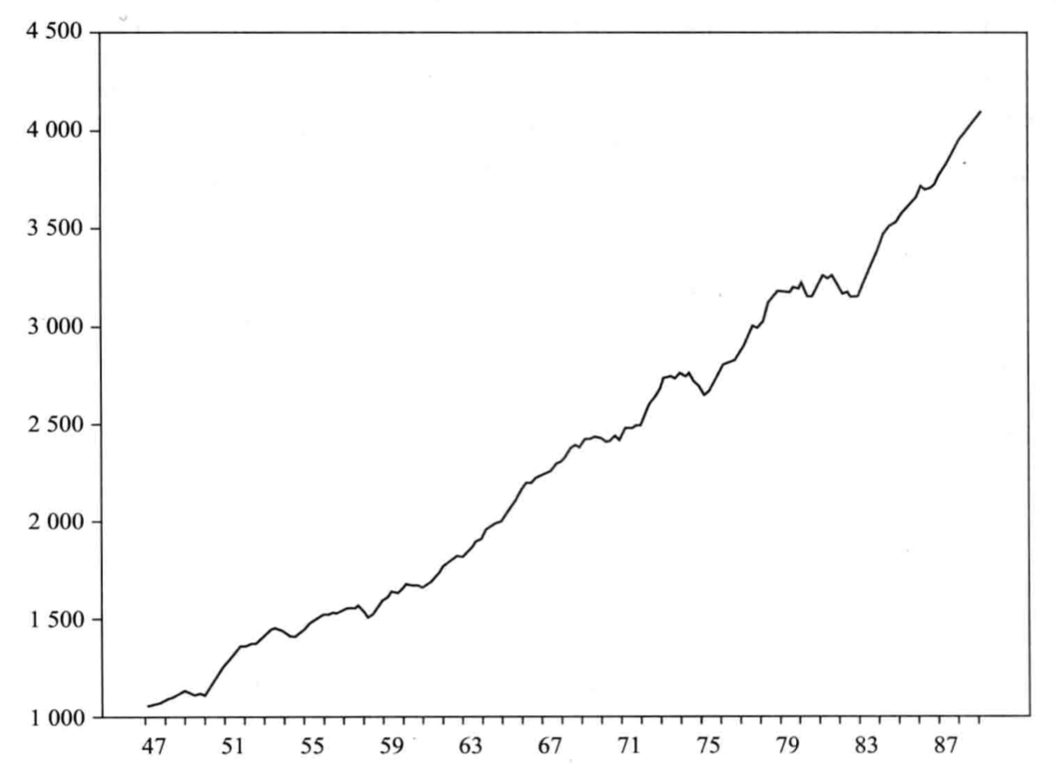
图2序列图显示序列一直是上升的,此序列要么是趋势平稳,要么是带漂移的随机游走。零假设自然是:序列是带漂移的随机游走,备择假设是:序列是趋势平稳过程。从正规步骤的步骤1开始,后面的步骤2和 1无须做,因为时序图表明这不可能是一个随机游走。
如果只是单纯检验系列是否包含单位根
使用正规检验步骤可以判断序列是否包含单位根,同时可以判断是A和B中的哪一种非平稳。如果我们只是简单想知道序列是否平包含单位根,那么有一个简单的方法,并且该方法无需做F检验,通过统计软件就可以实施。
同时使用三个模型做检验,如果任何一个模型出现平稳结果,则序列平稳,否则(3个模型都不拒绝零假设)序列包含单位根。嗯,简单粗暴,非常有效。中国人民大学王燕老师的《应用时间序列分析》一书中采用的就是这种方法。
《计量经济学-张晓峒》书中的错误单位根检验步骤
下面是该书的检验步骤

此处的12-22对应模型1,12-24对应模型2,12-25对应模型3,该书因为在模型方程两边都减去了 y_{t-1} ,所以序列如果存在单位根,则有 \rho=0 。
错误如下:
- 步骤1中的(1)错误,因为模型3的备择假设是:序列平稳或者趋势平稳,所以(1)这种情况根本就不存在,也就是不满足检验前提。
- 步骤1中的(2)出现,会接着进行步骤2。前文说过“ A和B,模型2的统计量分布是不同的”, 所以使用模型2必须首先选定你的生成过程到底是A和B中的哪一个才行。步骤2中的(1)出现,说明生成过程是B,步骤2中的(2)出现,说明生成过程是A,那么请问,步骤2的零假设到底是哪一个?逻辑混乱。
本人才疏学浅,如果文章观点存在错误或者疏漏,欢迎在评论区指出。
