手写SVM算法（Matlab实现）

1 年前

霁澂

support vector machine 作为机器学习里边理论最为漂亮的算法（没有之一），完美地融合了凸优化、数值分析、泛函、解析几何、高等代数，当初我也是花了好多时间才大概搞清楚了。当然，想要彻底搞懂这个算法，最好还是将算法手写一遍。这里的实现代码用的是matlab手写，主要原因是个人认为matlab对于线性代数的运算是十分友好的，而且对于非计算机专业的学生上手很快。最重要的是，机器学习涉及到的大量矩阵运算用matlab都十分容易实现， 比如矩阵乘法直接打*，矩阵转置直接打'，两个矩阵对应元素点乘直接打.*即可 ；相比python要用numpy库里的dot、divide、multipy简洁很多。

这里的代码分了两部分，一部分是针对线性可分的数据集，没有使用核函数；第二部分是针对环形数据集，使用了高斯核函数。整个代码最难的部分是二次规划的求解部分，我偷了一下懒，用的是matlab自带的quadprog函数。

对于SVM算法的原理，可以看这篇文章，讲得还是好的，既严谨又生动。

第一部分：

首先需要利用随机数模拟器生成一些数据，方便后边使用。这里是线性可分的数据集。

%支持向量机support vector machine%软间隔soft margin
%二次规划问题
%随机模拟一些点作分类用途
random=unifrnd(-1,1,50,2);
group1=ones(50,2)+random;%生成两个类别的变量
group2=2.85*ones(50,2)+random;
x=[group1;group2];
data=[group1,-1*ones(50,1);group2,1*ones(50,1)];%数据与对应标签
y=data(:,end);%真实类别

接着是代码的核心部分，因为根据理论，此时需要求解这样一个二次规划问题：

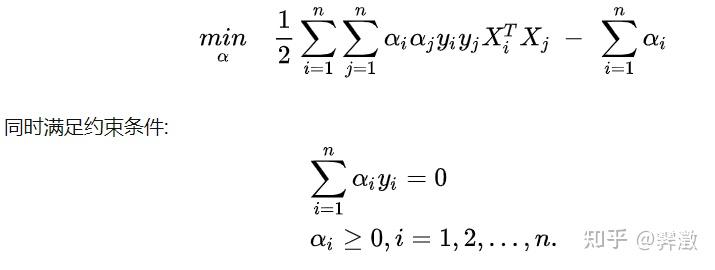
解这个问题常用的算法是SMO算法，但这个算法对于现在的我来说还是太难了。幸好matlab有一个内置的二次规划求解函数quadprog，故我们这里偷个懒直接调用这个函数对上述的alpha进行求解。

注意，matlab的quadprog函数有这样的使用要求：

目标函数必须写处一个二次型H和一个矩阵相加的形式。所以一定要根据它的要求输入参数。

h=[]%目标函数的H
for i=1:length(x)%对于所有样本都要遍历
    for j=1:length(x)
        h(i,j)=x(i,:)*(x(j,:))'*y(i)*y(j);
f=-1*ones(length(x),1);%目标函数的f

接下来是等式约束和不等式约束条件

%等式约束
aeq=y';
beq=zeros(1,1);
%不等式约束
ub=[];
ib=[];
%自变量约束
lb=zeros(length(x),1);
ub=[];
[a,fval]=quadprog(h,f,ib,ub,aeq,beq,lb,ub);%二次规划问题

那么a就是我们要求的alpha值。

这里要注意一下，利用quadprog函数求解出来的alpha值有很多是十分接近于0但却又不等于0，诸如10^-4（为何会这样我也不清楚），这些a对应的是非支持向量，故我们要先令它们全为零。

for i=1:length(a)
    if a(i)<1e-05
        a(i)=0;
end

接下来我们根据公式把超平面的系数w和b求出即可：

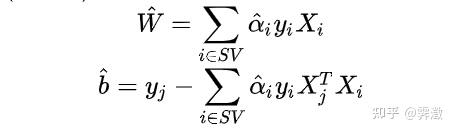
w=0;%系数矩阵
ff=find(a~=0)
j=ff(1)%寻找a系数不等于的下标j
for i=1:length(x)%关键系数数求解
    w=w+a(i)*y(i)*x(i,:)';
    u=u+a(i)*y(i)*(x(i,:)*x(j,:)');
b=y(j)-u;

至此，我们就已经手写完一个SVM算法，很简单，不是吗？

利用我们构建好的超平面，去检验训练集和测试集的效果，并得出一个准群率。这里只有训练集。

%分类决策函数作预测
predict=[];
for i=1:length(x)%预测第i个样本
    uu=0;%过度变量
    for j=1:length(x)%利用训练集的所有样本构建预测函数
        uu=uu+a(j)*y(j)*(x(j,:)*x(i,:)');
    result=sign(uu+b);
    predict(i,1)=result;
judge=(predict==y);
score=sum(judge)./length(data)

我们可以做一些可视化工作，检验效果。

%画出点以及对应的超平面
scatter(group1(:,1),group1(:,2),'red');
hold on
scatter(group2(:,1),group2(:,2),'blue');
hold on
k=-w(1)./w(2);%将直线改写成斜截式便于作图
bb=-b./w(2);
xx=0:4;
yy=k.*xx+bb;
plot(xx,yy,'-')
hold on
yy=k.*xx+bb+1./w(2)
plot(xx,yy,'--')
hold on
yy=k.*xx+bb-1./w(2)
plot(xx,yy,'--')
title('support vector machine')
xlabel('dimension1')
ylabel('dimension2')
legend('group1','group2','separating hyperplane')

效果图：

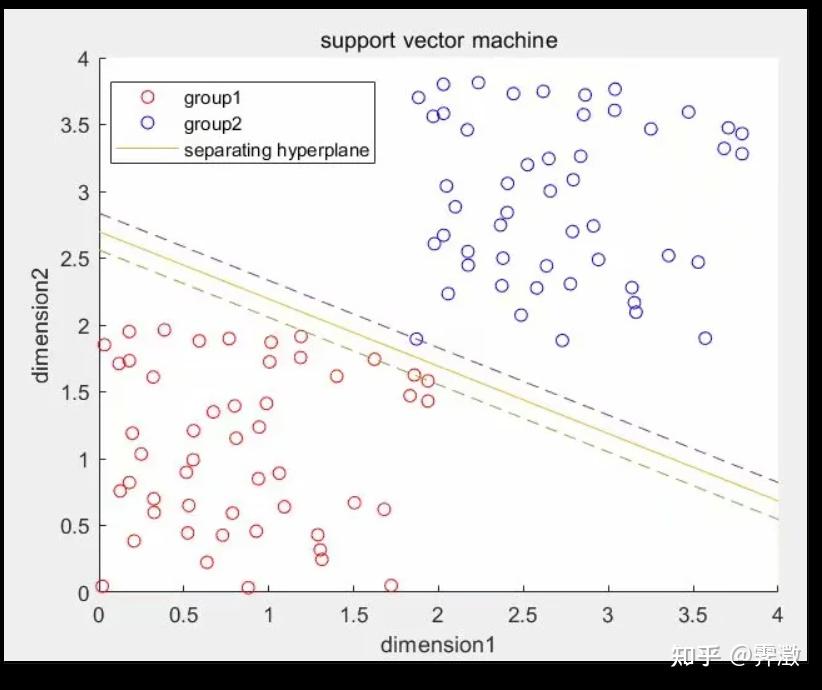
第二部分：（因为高斯核函数存在参数，需要利用学习曲线寻找最优参数，运行速度会偏慢）

上面的数据集是线性可分的，但要是面对线性不可分的数据集，就需要用核函数做高维映射了。比如我利用python sklearn库生成的环形数据集，这是标准化后的数据。（虽然有些滑稽，但在我学习机器学习的过程中，经常调取python库里的数据然后用matlab写代码，各取所长嘛）

#生成环形数据集
from sklearn.datasets import make_circles
import numpy as np
import pandas as pd
x,y=make_circles(n_samples=1000,factor=0.7,noise=0.1)
data=pd.DataFrame(x,columns=['x1','x2'])
data['label']=y
data.to_csv('circles_datasets1.csv')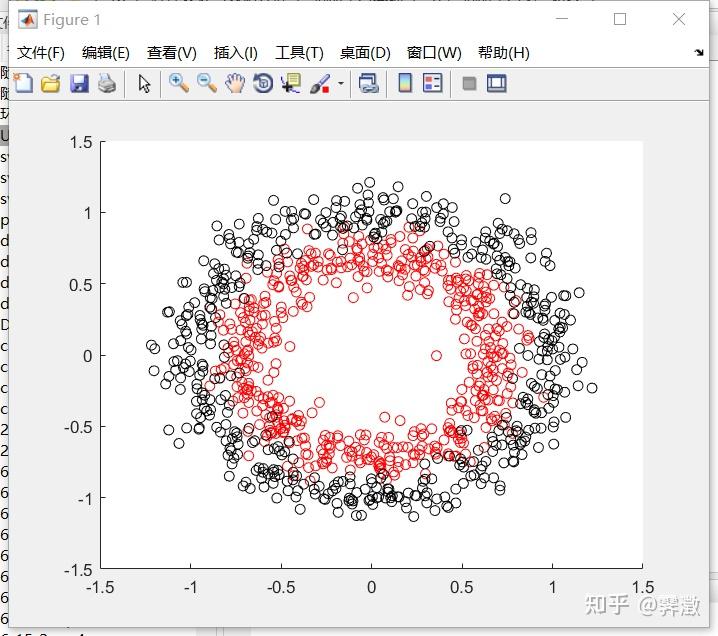

关于高维映射与核技巧，可以参考这篇文章：

这里我用的是RBF核函数（即高斯核函数）：

因为涉及到距离问题，所以读入数据后需要标准化：

%支持向量机support vector machine
%二次规划问题
%高维映射与核方法
data1=xlsread('circles_datasets1.xlsx','B2:D1001');
xx=data1(:,1:2);
xx=zscore(xx);%标准化
yy=data1(:,end);

还有就是将类类别划分为1和-1：

for i=1:length(yy)
    if yy(i)==0;%将类别划分为-1
        yy(i)=-1;
end

对于非线性支持向量机，选择了RBF核函数后就存在了一个超参数sigma,需要多次训练取最优值。我的做法是每次训练都重新划分训练集和测试集，增加随机性，以选出最优的sigma值。

data1=[xx,yy];
score1=[];
score2=[];
para=linspace(0.34,0.35,15)%生成不同的sigma值
for i=1:length(para)
 sigma=para(i)%设置高斯核函数参数
   %划分训练集和测试集
ratio=0.7%训练集比例
num=round(ratio*length(data1));
r=randperm(length(data1));%产生于样本数相同的随机数
num=round(ratio*length(data1));
train=data1(r(1:num),:);%训练集
test=data1(r(num+1:end),:)
x=train(:,1:end-1);%x、y代表训练集
y=train(:,end);
data=[x,y];

此时的最优化目标为：

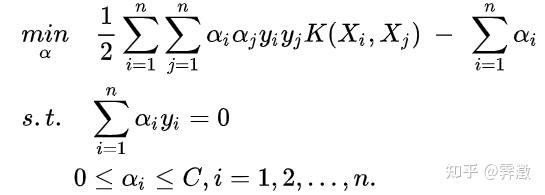
    k=[];%保存核函数对应下不同样本的内积值
for i=1:length(data)
    for j=1:length(data)
        norm2=(data(i,1:end-1)-data(j,1:end-1))*(data(i,1:end-1)-data(j,1:end-1))';
        k(i,j)=exp(-norm2./(2*sigma.^2)) ;
h=[]%目标函数的H
for i=1:length(x)%对于所有样本都要遍历
    for j=1:length(x)
        h(i,j)=k(i,j)*y(i)*y(j);
f=-1*ones(length(x),1);%目标函数的f
%等式约束
aeq=y'
beq=zeros(1,1);
%不等式约束
ub=[];
ib=[];
%自变量约束
lb=zeros(length(x),1);
ub=[];
[a,fval]=quadprog(h,f,ib,ub,aeq,beq,lb,ub);
w=0;%系数矩阵
for i=1:length(a)
    if a(i)<1e-05
        a(i)=0
end

再把超平面的参数计算出来：w同上，b为：

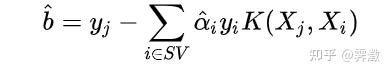
ff=find(a~=0)
j=ff(1)%寻找a系数不等于的下标j
for i=1:length(x);%关键系数数求解
    w=w+a(i)*y(i)*x(i,:)';
    u=u+a(i)*y(i)*(k(i,j));
b=y(j)-u;

接下来就是训练集和测试集的分数：

predict=[];%用于存储预测值
%训练集预测
for i=1:length(x)%预测第i个样本
    uu=0;%过度变量
    for j=1:length(x);%利用训练集的所有样本构建预测函数，预测训练集
        norm2=(data(j,1:end-1)-data(i,1:end-1))*(data(j,1:end-1)-data(i,1:end-1))';%L2范数
        kk=exp(-norm2./(2*sigma.^2));%高斯核函数
        uu=uu+a(j)*y(j)*kk;
    result=sign(uu+b);
    predict(i,1)=result;
judge=(predict==y);
trainscore=sum(judge)./length(data);
score1=[score1;trainscore];%记录训练集分数
x1=test(:,1:end-1);%x1、y1代表测试集
y1=test(:,end);
data2=[x1,y1];%测试集
%测试集预测
predict1=[];
for i=1:length(x1)%预测第i个样本
    uu=0;%过度变量
    for j=1:length(x);%利用训练集的所有样本构建预测函数,预测测试集
        norm2=(data(j,1:end-1)-data2(i,1:end-1))*(data(j,1:end-1)-data2(i,1:end-1))';%L2范数
        kk=exp(-norm2./(2*sigma.^2));
        uu=uu+a(j)*y(j)*kk;
    result=sign(uu+b);
    predict1(i,1)=result;
judge1=(predict1==y1);
testscore=sum(judge1)./length(data2)
score2=[score2;testscore];