MATLAB：Simulink基础
视频教学：
https://www.zhihu.com/video/1454912983461367809
第一次录制教学视频，有点紧张，说话有吞吐、卡顿和模糊等一系列问题，下次会改进的
概要：
- Simulink 是图形化编程，通过模块之间的连接实现代码功能
- Simulink 的模块库有很多，分标注模块库 和 专业模块库
- 一般用Simulink编程时，少不了输入和输出模块
- Simulink的子系统 相当于 程序语言中的函数
Simulink
SIMULINK： 是MATLAB的一个分支产品，主要用来实现对工程问题的 模块化 及 动态仿真
一、添加内容：
1.从模块库中添加：
模块库： 包含 标准模块库 和 专业模块库
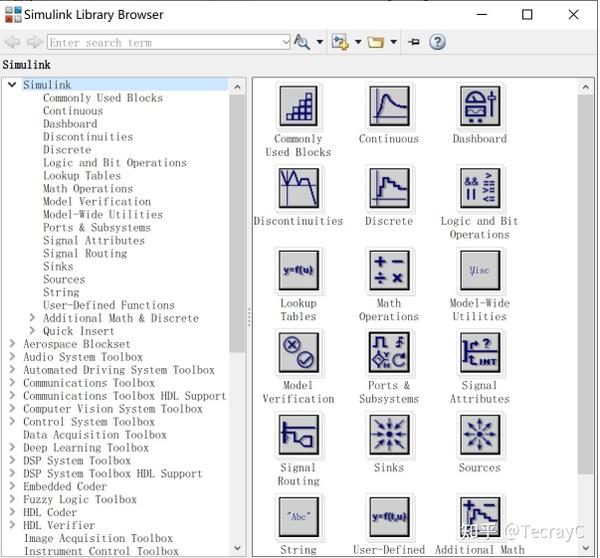
2.在面板中 双击 输入模块名字添加（本人常用）
二、常规操作：
连线分支： 按住Ctrl
标签： 双击
- Format 改参数
注释模块： %
旋转： Ctrl+R
水平翻转： Ctrl+i
三、常用模块：
模块的属性可以通过双击修改
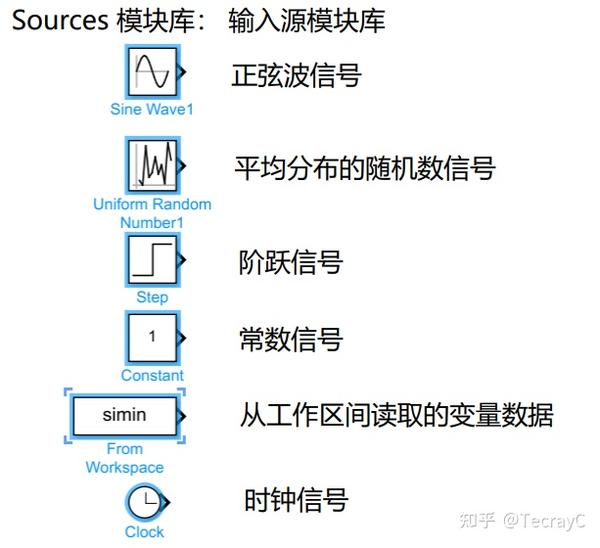
1.输入模块：Sources模块库
2.输出模块：Sinks模块库
其中，To File 输出文件路径是 ”当前文件夹“
3.计算模块：Math模块库
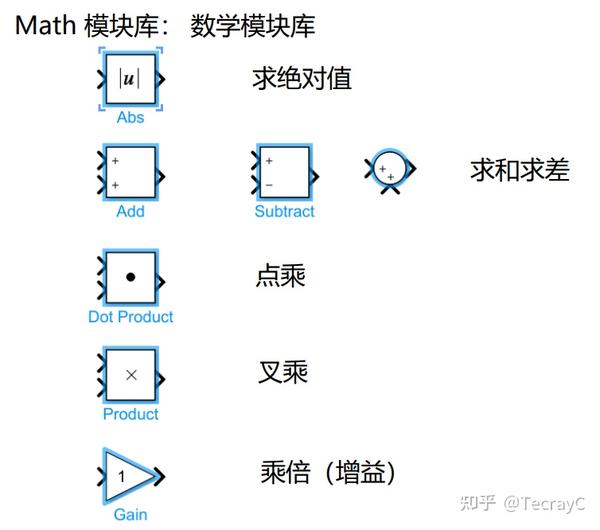
4.比较模块库： Logic and Bit Operations
5.连续系统模块库： Continuous
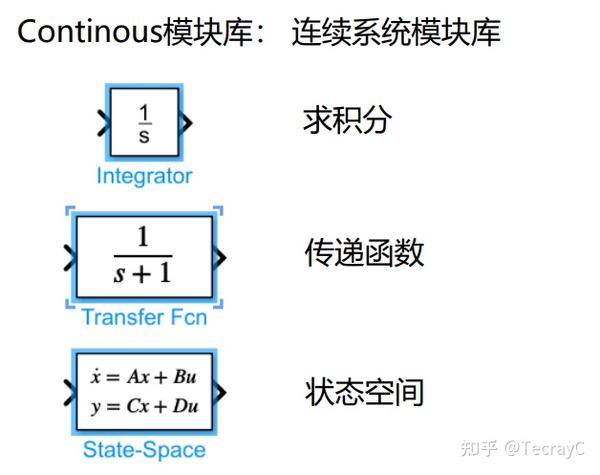
需要注意的是，Simlulink输出的结果是实时计算的结果，这里的积分也可以理解为定积分，下限是仿真参数的Start time，上限是实时的，直到计算到最后的Stop time
例子：求 sin(t)在-2~7的定积分，可以这么写
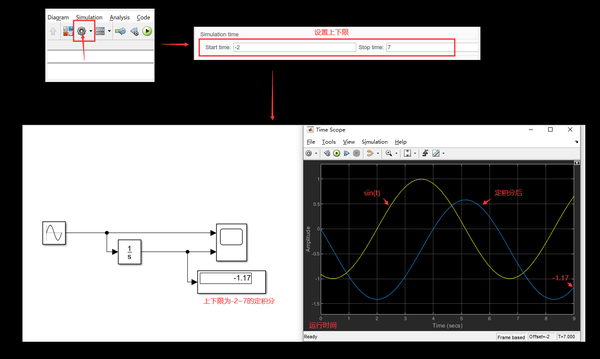
四、子系统:
子系统： 将多个模块封装为一个子系统，相当于封装成一个函数。
- 子系统的输入：In模块
- 子系统的输出：Out模块
子系统的建立
- 法一：框选模块——Create Subsystem from selection
- 法二：添加 Subsystem 模块
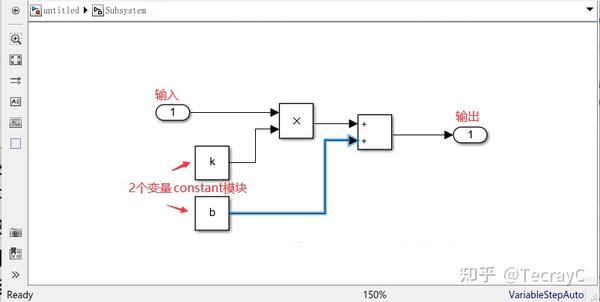
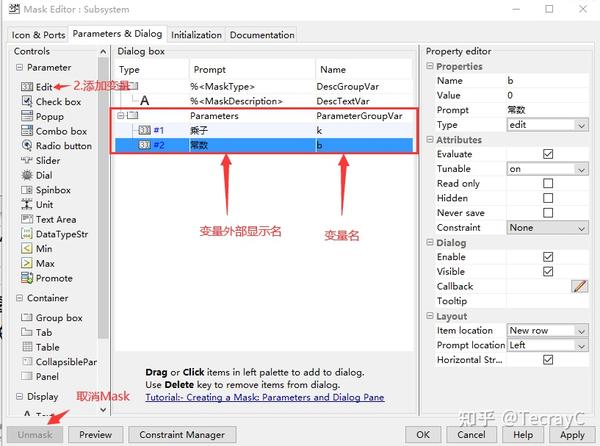
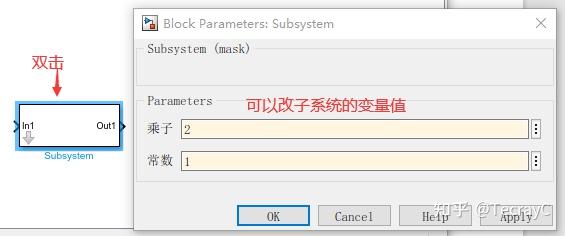
子系统的封装变量设置：
- 右击子系统 Mask
五、运行仿真参数设置
进入设置：
- 法一：菜单选项 [Simulation>Model Configuration Parameters]
- 法二：点击 ”齿轮“ 设置
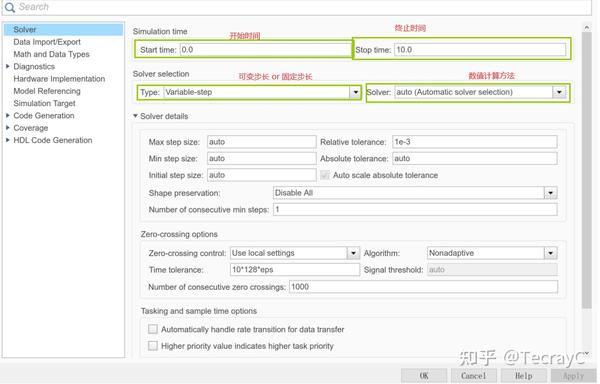
仿真时间设置：
- Start time：仿真开始时间
- Stop time：仿真结束时间
选择仿真算法：
仿真算法是求常微分方程、传递函数、状态方程解的数值计算方法
- Variable Step：可变步长算法，在仿真过程中可以自动调 整步长，并通过减小步长来提高计算的精度
- Fixed Step：固定步长类算法，在仿真过程中采取基准采样 时间作为固定步长
一般而言，使用 变步长的自适应算法 是比较好的选择。这类算法会按照设定的精确度在各积分段内自适应地寻找最大步长进行积分， 从而使得效率最高
六、Simulink案例
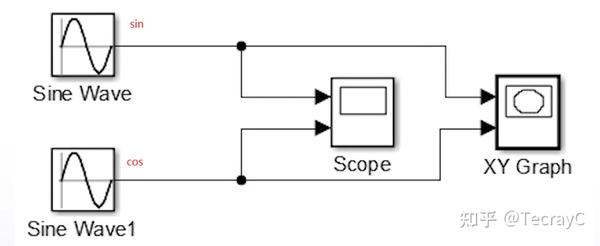
例1：
- 分别显示曲线 y=sin(t) 和 y=cos(t)
- 同时显示 sin(t) 对 cos(t) 的变化曲线 ,即 sin(t)^2+cos(t)^2 =1
解：
——————————————————————
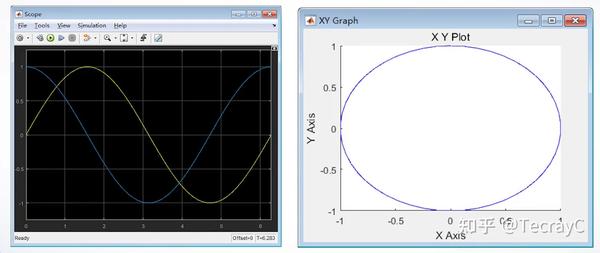
例2：
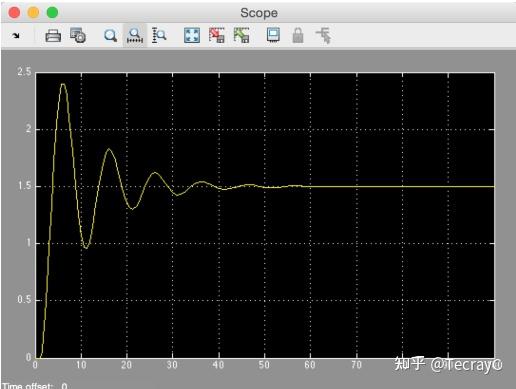
求解： x'' + 0.2x' + 0.4x = 0.2u(t) ,其中， u(t) 为输入阶跃信号，求系统的输出响应 x
方法一： simulink微分方程仿真
- 将原函数改写为 x'' = 0.2u(t)-0.2x'-0.4x
- 用 积分模块 构造微分方程求解模型 \stackrel{··}{x}\stackrel{\int}{\longrightarrow} \stackrel{·}{x}\stackrel{\int}{\longrightarrow} x
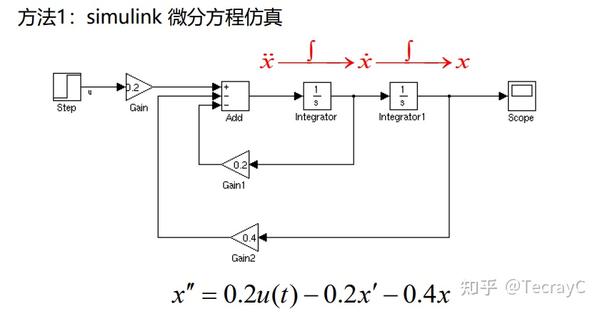
方法二： simulink 传递函数仿真
(s^2 + 0.2s +0.4)C(s) = 0.2R(s)
G(s) = \frac{C(s)}{R(s)}=\frac{0.2}{s^2+0.2s+0.4} G(s) 为传递函数
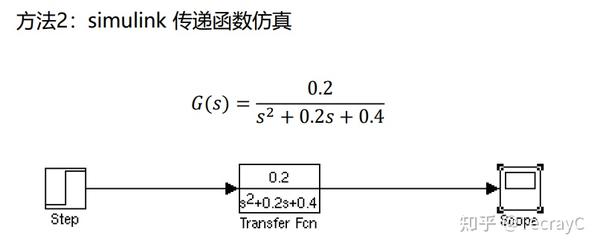
方法三： simulink状态方程仿真
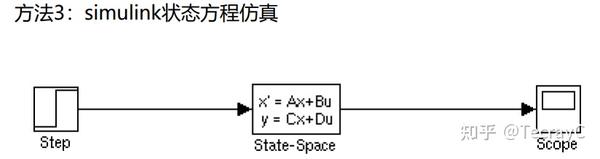
输出结果：
七、补充例题
例题1
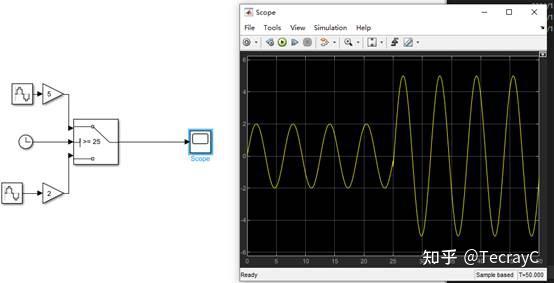
使用Simulink仿真 y(t)=\left\{ \begin{array}{ll} 5sin(t),t\geqslant25\\2sin(t),t<25 \end{array} \right.
解：
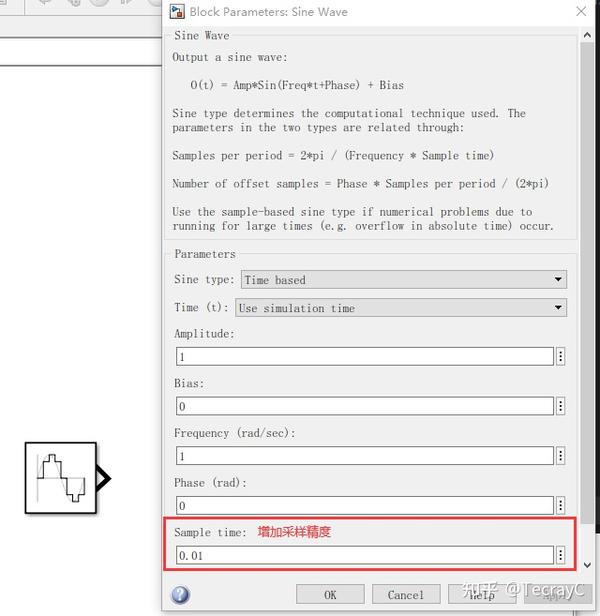
改善波形：
——————————————————————————————————————
例题2
使用simulink求解微分方程
\left\{ \begin{array}{ll} \frac{d^2x}{dt^2}-1000(1-x^2)\frac{dx}{dt}+x=0\\x(0)=2\\x'(0)=0 \end{array} \right.
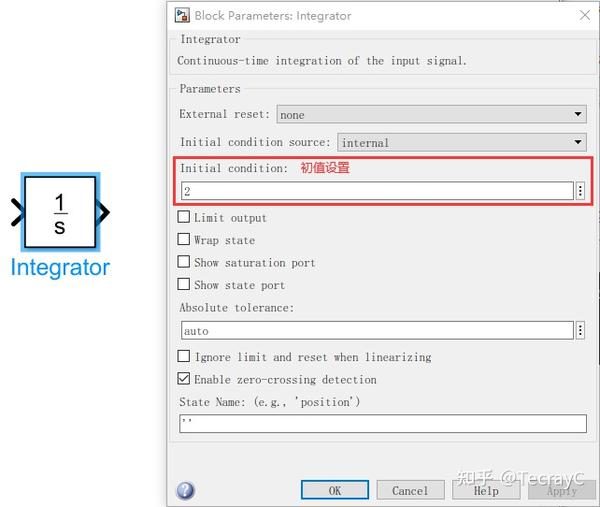
解：将 \frac{d^2x}{dt^2} 移到一边，得 x''(t)=1000(1-x^2)x'-x
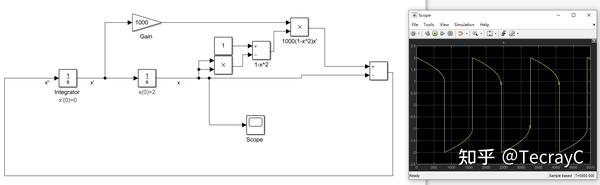
初值设置
在外部显示初值：右键->Properties->Block Annotation->
——————————————————————————————————————
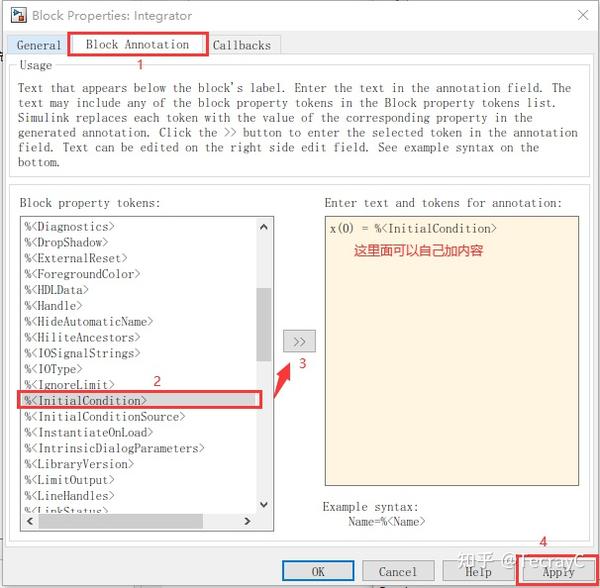
例题3
建立一个简单模型，产生一组常数（1x5），再将该常数与其5倍的结果合成一个二维数组，用数字显示器显示出来
解：
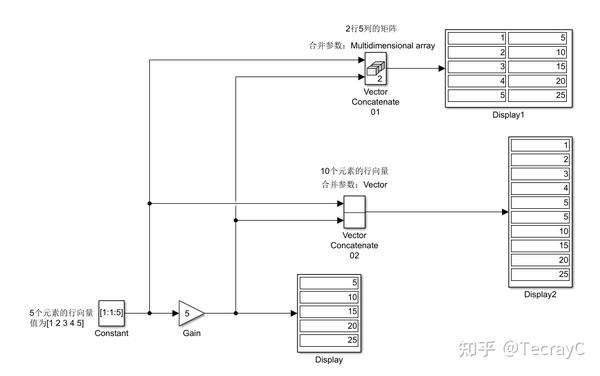
Vector Concatenate的参数设置
——————————————————————————————————————
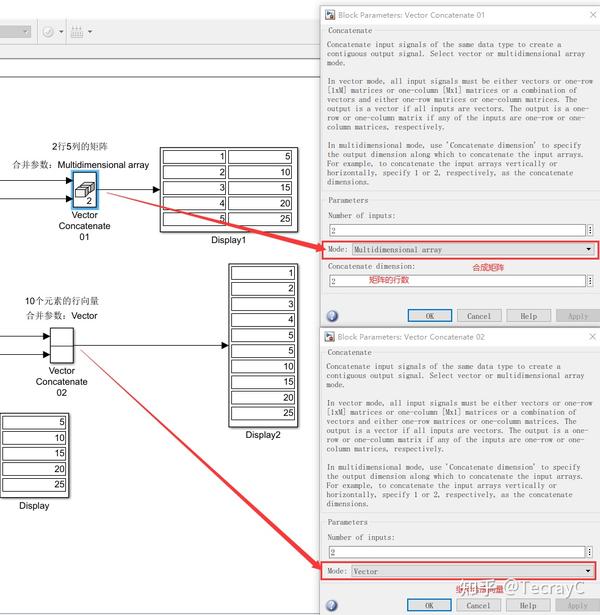
例题4·电路1
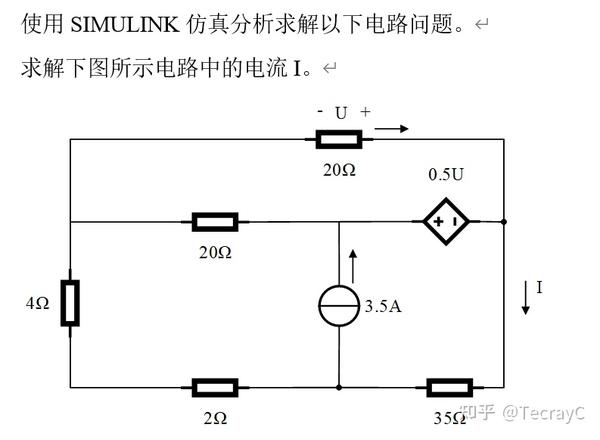
解法一：蓝色电路
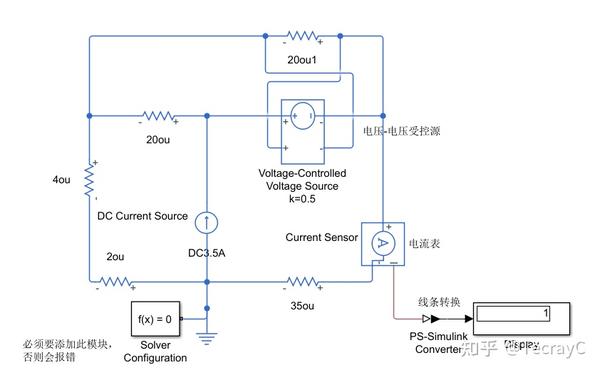
解法一所用模块：
注意：用此蓝色的电路必须要添加 Solver Configuration 到接地端，且数值显示需要线条转换
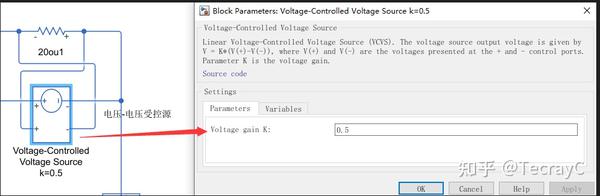
受控电压源参数设置，k=0.5
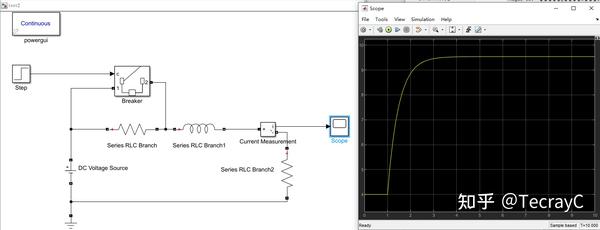
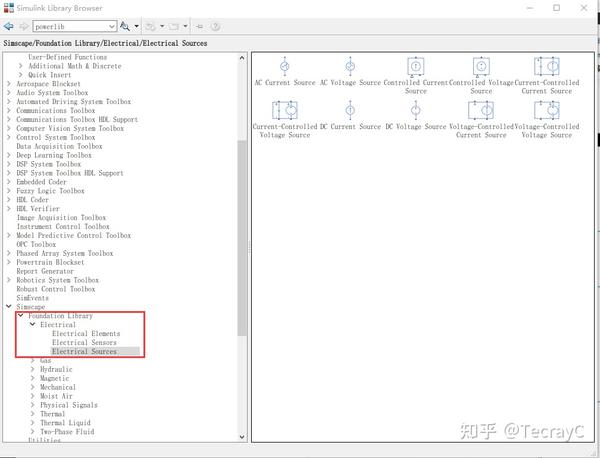
解法二：用 powerlib模块库 里的黑色电路
注意：需要添加powergui
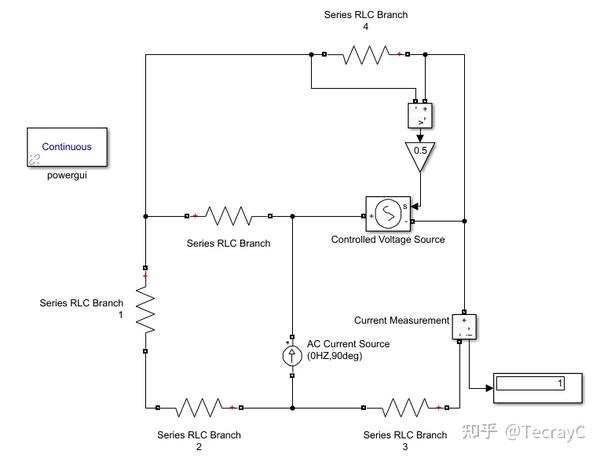
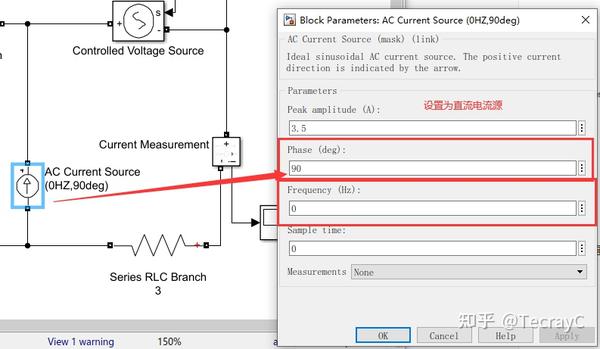
此电路无直流电流源，因此需要将交流源改为直流：F频率设置为0，相角设置为90度
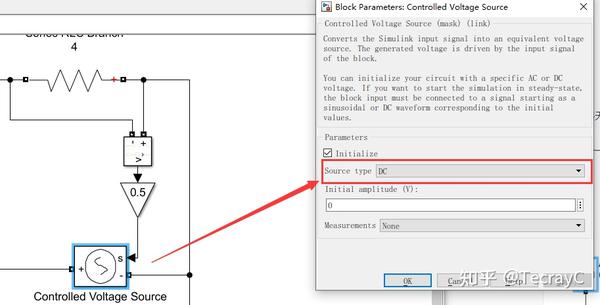
电压-电压受控源也需要设置为直流
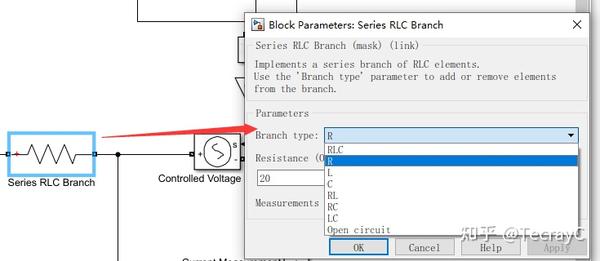
电阻设置：这里只有电阻，所以只选择R
——————————————————————————————————————
例题5·电路2
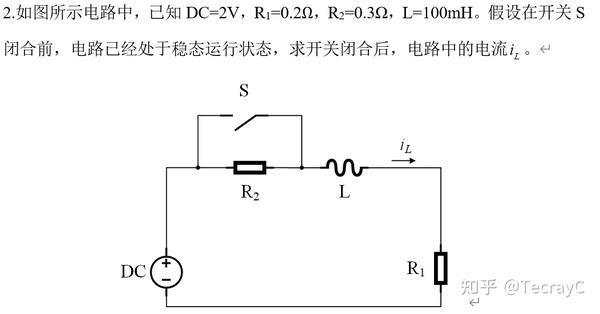
解：
