对比这个测试集的“Correctly Classified Instances”(55.7 %)与训练集的“Correctly Classified Instances”(59.1 %),我们看到此模型的准确性非常接近,这表明此模型不会在应用未知数据或未来数据时,发生故障。
不过,由于模型的准确性很差,只能正确地分类 60 % 的数据记录,因此我们可以后退一步说:“哦,这个模型一点都不好。其准确性勉强超过 50 %,我随便猜猜,也能得到这样的准确性。”这完全正确。这也是我想审慎地告诉大家的一点:有时候,将数据挖掘算法应用到数据集有可能会生成一个糟糕的模型。这一点在这里尤其准确,并且它是故意的。
我本想带您亲历用适合于分类模型的数据生成一个分类树的全过程。然而,我们从 WEKA 获得的结果表明我们错了。我们在这里本应选择的并非 分类树。我们所创建的这个模型不能告诉我们任何信息,并且如果我们使用它,我们可能会做出错误的决策并浪费钱财。
那么这是不是意味着该数据无法被挖掘呢?当然不是,只不过需要使用另一种数据挖掘方法:最近邻模型,该模型会在本系列的后续文章中讨论,它使用相同的数据集,却能创建一个准确性超过 88 % 的模型。它旨在强调一点:那就是必须为数据选择合适的模型才能得到有意义的信息。
Halcon是德国MVTec公司开发的一套完善的机器视觉算法包,也是一款功能强大的视觉处理软件,为工业自动化领域提供了全面的解决方案。以下是关于Halcon的详细介绍:
1、概述:
- Halcon提供了一套丰富的图像处理和机器视觉算法,可以在各种工业应用中进行图像分析、目标检测、测量、定位、识别等任务。
- 其核心功能包括图像处理、特征提取与匹配、3D视觉、深度学习、条码识别、OCR识别以及视觉测量等。
2、技术特点:
- 支持Windows、Linux和Mac OS X操作环境,保证了投资的有效性。
- 提供了与多种编程语言(如C、C++、C#、Visual Basic和Delphi等)的接口,便于用户集成和定制。
- 坐标定义遵循右手坐标系,原点位于图像的左上角,X轴水平向右延伸,Y轴垂直向下延伸。
3、应用领域:
- 自动化生产、工业检测、医药制造、智能交通、安防监控等。
- 医学图像分析、无人驾驶、智能机器人等领域,帮助实现更智能化和自动化的生产和服务。
4、版本更新:
以HALCON 11为例,其新功能包括:
- 技术革新:基于样本的识别方法可以区分出数量巨大的目标对象,实现真正意义上的目标识别。
- 强大的三维视觉处理:提供三维表面比较技术,支持多种三维目标处理的方法。
- 高速机器视觉体验:支持使用GPU处理进行机器视觉算法的算子超过75个,提供高速的机器视觉体验。
5、优势:
- HALCON在欧洲以及日本的工业界被认为是具有最佳效能的Machine Vision软件。
- 源自学术界,其图像处理库由一千多个各自独立的函数和底层的数据管理核心构成,具有强大的计算和分析能力。
6、名称来源:
- Halcon的名称来自于“HALf CmOS ON a Chip(一个芯片上的半CMOS)”一词的缩写,同时也来自于西班牙语中的“鹰”一词,寓意坚定、精力充沛、机敏等。
综上所述,Halcon是一款功能强大、应用广泛的机器视觉算法包和视觉处理软件,为工业自动化和图像处理领域提供了全面的解决方案。
参考C4.5算法详解(非常仔细)用 WEKA 进行数据挖掘,第 2 部分weka算法参数整理文章目录1 算法原理1.1 计算类别信息熵1.2 计算每个属性的信息熵1.3 计算信息增益1.4 计算属性分裂信息度量1.5 计算信息增益率2 weka上的实现2.1 WEKA 数据集2.2 在 WEKA 内进行分类1 算法原理 首先,C4.5是决策树算法的一种。决策树算法作为一种分类算法,...
基于weka的数据分类分析实验报告 1 实验目的 (1)了解决策树C4.5和朴素贝叶斯等算法的基本原理。 (2)熟练使用weka实现上述两种数据挖掘算法,并对训练出的模型进行测试和评价 。 2 实验基本内容 本实验的基本内容是通过基于weka实现两种常见的数据挖掘算法(决策树C4.5和朴素 贝叶斯),分别在训练数据上训练出分类模型,并使用校验数据对各个模型进行测试和 评价,找出各个模型最优的参数值,并对模型进行全面评价比较,得到一个最好的分类 模型以及该模型所有设置的最优参数。最后使用这些参数以及训练集和校验集数据一起 构造出一个最优分类器,并利用该分类器对测试数据进行预测。 3 算法基本原理 (1)决策树C4.5 C4.5是一系列用在机器学习和数据挖掘的分类问题中的算法。它的目标是监督学习: 给定一个数据集,其中的每一个元组都能用一组属性值来描述,每一个元组属于一个互 斥的类别中的某一类。C4.5的目标是通过学习,找到一个从属性值到类别的映射关系, 并且这个映射能用于对新的类别未知的实体进行分类。C4.5由J.Ross Quinlan在ID3的基础上提出的。ID3算法用来构造决策树。决策树是一种类似流程图的树 结构,其中每个内部节点(非树叶节点)表示在一个属性上的测试,每个分枝代表一个 测试输出,而每个树叶节点存放一个类标号。一旦建立好了决策树,对于一个未给定类 标号的元组,跟踪一条有根节点到叶节点的路径,该叶节点就存放着该元组的预测。决 策树的优势在于不需要任何领域知识或参数设置,适合于探测性的知识发现。 从ID3算法中衍生出了C4.5和CART两种算法,这两种算法在数据挖掘中都非常重要。 属性选择度量又称分裂规则,因为它们决定给定节点上的元组如何分裂。属性选择度 量提供了每个属性描述给定训练元组的秩评定,具有最好度量得分的属性被选作给定元 组的分裂属性。目前比较流行的属性选择度量有--信息增益、增益率和Gini指标。 (2)朴素贝叶斯 贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶 斯分类。 朴素贝叶斯分类是一种十分简单的分类算法,叫它朴素贝叶斯分类是因为这种方法的 思想真的很朴素,朴素贝叶斯的思想基础是这样的:对于给出的待分类项,求解在此项 出现的条件下各个类别出现的概率,哪个最大,就认为此待分类项属于哪个类别。通俗 来说,就好比这么个道理,你在街上看到一个黑人,我问你你猜这哥们哪里来的,你十 有八九猜非洲。为什么呢?因为黑人中非洲人的比率最高,当然人家也可能是美洲人或 亚洲人,但在没有其它可用信息下,我们会选择条件概率最大的类别,这就是朴素贝叶 斯的思想基础。 朴素贝叶斯分类的正式定义如下: 1)设x={a_1,a_2,...,a_m}为一个待分类项,而每个a为x的一个特征属性。 2)有类别集合C={y_1,y_2,...,y_n}。 3)计算P(y_1"x),P(y_2"x),...,P(y_n"x)。 4)如果P(y_k"x)=max{P(y_1"x),P(y_2"x),...,P(y_n"x)},则x in y_k。 那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做: 1)找到一个已知分类的待分类项集合,这个集合叫做训练样本集。 2)统计得到在各类别下各个特征属性的条件概率估计。即P(a_1"y_1),P(a_2"y_1), ...,P(a_m"y_1);P(a_1"y_2),P(a_2"y_2),...,P(a_m"y_2);...;P(a_1"y_n),P(a_2"y_n ),...,P(a_m"y_n)。 3)如果各个特征属性是条件独立的,则根据贝叶斯定理有如下推导: P(y_i"x)=frac{P(x"y_i)P(y_i)}{P(x)} 因为分母对于所有类别为常数,因为我们只要将分子最大化皆可。又因为各特征属性 是条件独立的,所以有:P(x"y_i)P(y_i)=P(a_1"y_i)P(a_2"y_i)...P(a_m"y_i)P(y_i) =P(y_i)\prod^m_{j=1}P(a_j"y_i) 根据上述分析,朴素贝叶斯分类的流程分为三个阶段: 第一阶段——准备工作阶段,这个阶段的任务是为朴素贝叶斯分类做必要的准备,主要 工作是根据具体情况确定特征属性,并对每个特征属性进行适当划分,然后由人工对一 部分待分类项进行分类,形成训练样本集合。这一阶段的输入是所有待分类数据,输出 是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段, 其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分 及训练样本质量决定。 第二阶段——分类器训练阶段,这个阶段的任务就是生成分类器,主要工作是计算每个 类别在训练样本中的出现频率及
1、weka来源
WEKA的全名是怀卡托智能分析环境(Waikato Environment for Knowledge Analysis),同时weka也是新西兰的一种鸟名,而WEKA的主要开发者来自新西兰。WEKA作为一个公开的数据挖掘工作平台,集合了大量能承担数据挖掘任务的机器学习算法,包括对数据进行预处理,分类,回归、聚类、关联规则以及在新的交互式界面上的可视化。
2、...
这篇文章中我会通过几个例子向大家介绍一些weka中经典的数据挖掘算法和评估算法的手段。
J4.8 决策树算法
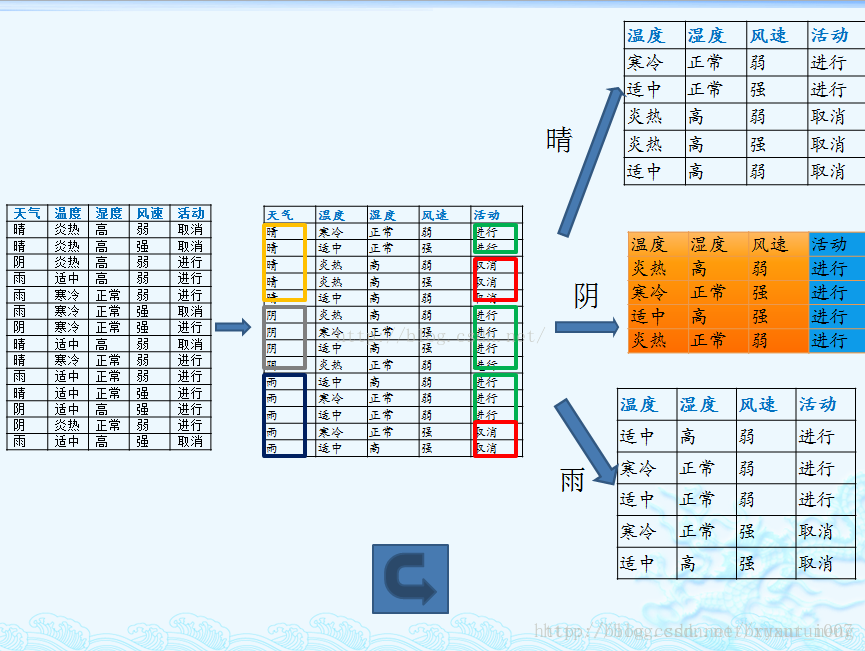
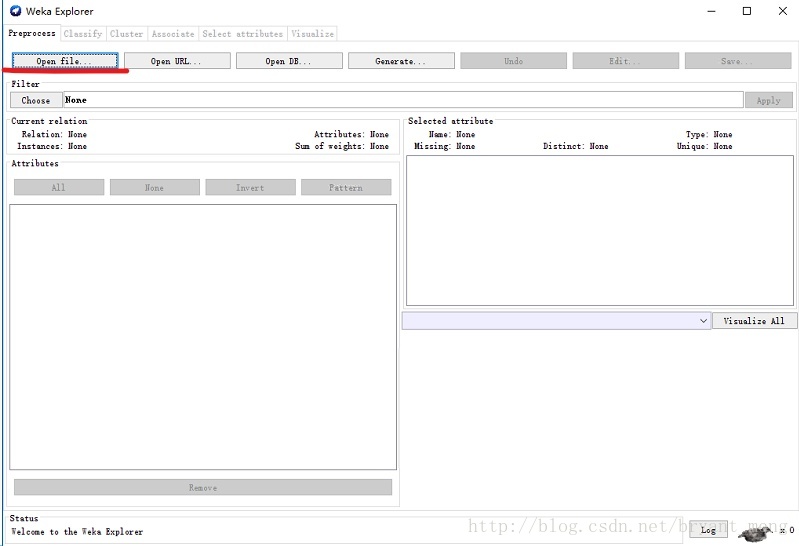
在预处理标签页 点击 open file ,选择 Weka 安装目录下 data 文件夹中的 weather.numberic.arff 。(在这个目录中有很多经典的样本)
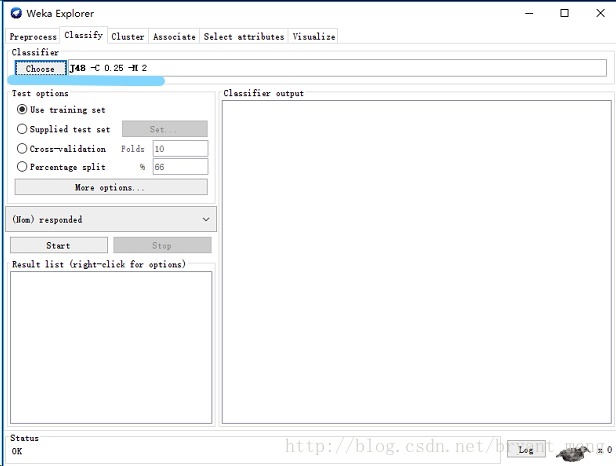
进入分类器标签,点击 Choose 按钮,开始选择分类器算法。在弹出的树状目录中找到 trees 节点...
如果您已经使用C4.5算法生成了决策树模型(例如,使用Weka),并且想在Matlab中使用该模型进行预测,可以按照以下步骤:
1. 将决策树模型保存为文件(例如,.model文件)。
2. 在Matlab中加载文件,并使用read_model函数将其读入Matlab中的结构体中。
3. 使用test_model函数对新数据进行分类预测。
以下是一个简单的示例代码:
```matlab
% 1. 读取决策树模型文件
model = load('c4.5.model', '-mat');
% 2. 将读入的结构体转换为决策树模型对象
c45 = ClassificationTree.fit(model.x, model.y, 'SplitCriterion', 'deviance');
% 3. 加载测试数据
test_data = load('test_data.mat', '-mat');
% 4. 对测试数据进行预测
predicted_labels = predict(c45, test_data.x);
在上述代码中,'c4.5.model'是您保存的决策树模型文件名,'test_data.mat'是包含测试数据的.mat文件名。在test_data.mat文件中,您需要将测试数据保存在一个名为'x'的变量中,将测试标签保存在一个名为'y'的变量中。
请注意,您需要在Matlab中安装'Classification Learner'工具箱才能使用ClassificationTree.fit和predict函数。