Shader学习（8）各种坐标空间的定义和变换演示

文中内容主要参考书籍《unity shader入门精要》，作者为冯乐乐。

该篇建议先浏览前面篇章的渲染流水线部分结合理解。

一、模型空间（model space）

模型空间（model space）在不同的游戏引擎或者是软件中又称作对象空间（object space）或者局部空间（local space）。

在游戏中的每一个模型或者物体都有各自独立的坐标空间，模型有自己的前后左右，这是它的自身属性，旋转或者是移动和缩放模型并不能改变它的前后左右。

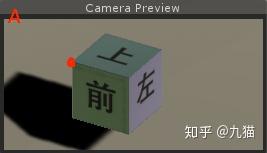
在Unity中，模型空间使用的是左手坐标系，因此在模型空间中，+x轴+y轴+z轴分别对应的是模型的右，上和前向。如上图。

模型的顶点坐标是根据模型空间的原点定义的，在上图中的正方体中，模型空间的原点就在模型的几何中心，但是模型空间的原点是可以编辑的，在很多其他模型中，原点可以是任何位置。

当模型放在场景中之后，就会产生一个基于模型原点模型空间。因为模型的长宽高都是1，上面的正方体上的一点A点在模型空间中的坐标为（0.5，0.5，0.5）。

二、世界空间（world space）

世界空间是最外层的空间，可以被用于描述绝对位置，这个绝对位置的概念类似于在我们现实世界的经度纬度海拔，而前一部分说的模型坐标则可以理解为个人的前后左右。

在Unity编辑场景时，选中一个模型的细节面板，其中的Transform属性栏表示的就是模型原点在世界空间中进行的变换。

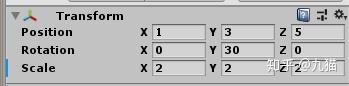
比如我们之前的正方体的坐标就如上图显示。

在渲染中，顶点变换的第一步就是把顶点从模型空间转换到世界空间。空间变换的第一步就是要构建变换矩阵。构建变换矩阵其实就是根据子空间原点在父空间中进行的变换来再对顶点进行一次同样的变换。

根据上图的ransform属性栏可以看出，模型在世界坐标下进行了（2，2，2）的缩放，围绕y轴旋转了30度，还被移动了（1，3，5）个单位。那么就可以计算变换矩阵M model->world：

在这里需要注意的是，看Transform面板的时候是从下往上看的，最先做缩放，再旋转，再移动。而在计算变换矩阵的时候，最后做的动作放在最左边，最先做的动作放在最右边。

有了如上的变换矩阵就可以对A点进行空间变换了。

所以，A点在世界空间中的坐标就是（2.366， 4， 5.366）。

如果要从世界空间再变回模型空间的话，很明显是不能直接转置整个M model->world变换矩阵的，因为他不是正交矩阵。根据定理：1.正交矩阵的转置矩阵等于它的逆矩阵2.一个矩阵的逆矩阵和它本身相乘结果是一个单位矩阵。我们可以验证一下这个矩阵：

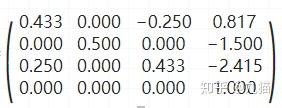
这个矩阵真正的逆矩阵其实是需要用逆矩阵求法如初等变换法等方式求出的，而这个数学过程太复杂所以适可而止。它最终的逆矩阵如下：

三、观察空间（view space）

观察空间也叫做摄像机空间（camera space）。观察空间的原点就是摄像机的位置，摄像机在哪里，观察空间原点就在哪里。

观察空间中，原点是摄像机位置，+x轴指向右方，+y轴指向上方，+z轴指向后方。需要注意的是摄像机的前方是-z轴，因为unity中观察空间使用的是右手坐标系，模型空间和世界空间使用的是左手坐标系，这个只需要记住就行了。

在渲染流程中，顶点变换的第二步就是把顶点从世界空间变换到观察空间中，这个变换叫做 观察变换（view transform） 。

观察变换的过程其实是和模型空间到世界空间的变换相似的，首先需要知道摄像机的变换信息：

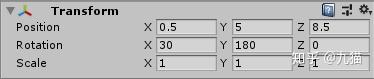
在观察变换的时候，是把世界空间作为观察空间的子空间来变换的，因此，我们可以把对摄像机的 变换想象为对世界空间的变换。根据上图，世界空间的原点从观察空间的原点出发进行了（-30， -180， 0）的旋转，然后又进行了（-0.5，-5，-8.5）的移动。由此我们可以构建变换矩阵以求出A点在观察空间中的坐标。

（需要注意的是上面的矩阵运算时是从右往左算的）

但是因为Unity中的观察空间使用的是右手坐标系，和左手坐标系的z轴相反，所以还是要乘以另一个特殊矩阵来得到正确的结果：

所以A点在观察空间中的坐标为：

四、裁剪空间（clip space）

裁剪空间也称作齐次裁剪空间，把顶点从观察空间转换到裁剪空间中的矩阵叫做裁剪矩阵，也被称作投影矩阵。

我们最终在摄像机中可以看到的区域是由视锥体决定的，视锥体就是我们可以看到的部分在计算机中的几何抽象，视锥体的边界以外的部分不渲染。视锥体由六个平面包围而成，这些平面被称作裁剪平面。

视锥体有两种投影类型：一种是正交投影（平行投影），一种是透视投影。

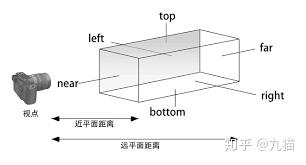
视锥体的六个平面当中，上下左右四个平面相当于望远镜的镜筒，而近裁剪平面和远裁剪平面则决定了你可以看到的最近和最远的距离。所有位于视锥体之内的物体将会被渲染，否则就会被裁剪而不能进入下一个环节。

正交投影的视锥体是一个长方体，而透视投影的视锥体是一个四棱锥，对于透视投影，要想判断顶点是否在一个锥体中是比较麻烦的，所以我们需要先通过一个投影矩阵把顶点转换到一个裁剪空间中。

视锥体是由六个裁剪平面定义的，在Unity中这六个平面主要由摄像机组件中的参数和窗口的纵横比共同决定。

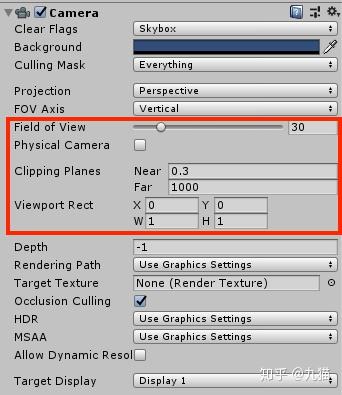
Field of View控制视锥体竖直张开的角度，调高之后甚至有鱼眼镜头的效果。Clipping Planes中的Near和Far控制视锥体的远近裁剪平面到摄像机的距离。通过公式可以得知视锥体的远近裁剪平面的高度。

根据以上公式，我们可以算出当前摄像机的远近裁剪平面的高度（根据上图中的摄像机数据）。

裁剪平面的高度知道之后，可以通过摄像机的纵横比来求出它的横向的长度。以目前大部分屏幕的长宽比16：9来计算我们现在的远近裁剪平面的长度，可以得到近裁剪平面长：0.284 ， 远裁剪平面的长度为:952.889 。

要构建由观察空间变换到裁剪空间的矩阵，需要知道摄像机面板的near、far和FOV三个数值。还需要计算出摄像机的纵横比Aspect，比如16：9 。

根据以上这些数值可以确定投影矩阵:

根据这个公式可以实际计算一下当前的变换矩阵：

一个顶点和投影矩阵相乘之后，就可以由观察空间变换到裁剪空间中。在前面的部分中已经得到了点A在观察空间中的坐标（-1.866 ， 0.701 ， -3.214）。接下来可以和这个变换矩阵相乘得到结果。

根据以上公式来计算一下变换结果。

从结果可以看出顶点的w分量不再是1，而是变成了原先z分量的相反数。现在，该w分量就可以用作判断一个顶点是否位于视锥体内，判断公式如下：

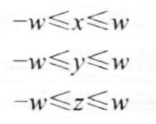
任何不满足上述条件的顶点将会被裁剪掉。现在A点的w分量为3.214，很明显不满足条件，所以被裁剪掉了。在Unity中显示的效果如下：

还需要注意的就是，经过裁剪矩阵的变换之后，裁剪空间变成了左手坐标系，而不再是观察空间中的右手坐标系。这意味着离摄像机越远，z值越大。

由于A点被裁剪掉了，所以接下来将使用上图中的B点继续转换。在上文中已经把所有的变换矩阵都计算了出来，B点和A点进行了相同的变换，可以直接用前文的矩阵计算B点。现在已知B点在模型空间中的坐标为：（-0.5， 0.5， 0.5） 。

上面计算了透视投影的计算方式，接下来了解一下正交投影的计算方式。

正交投影的视锥体是一个长方体，因此，计算正交投影的远近裁剪平面要更简单一些。

在原本的摄像机位置创建一个新的正交摄像机如下图

该摄像机的属性如下：

根据摄像机的属性，可以求出视锥体的远近裁剪平面的高度，公式如下：

所以远近裁剪平面的高度都是4。

横向的长度计算方式和前面透视投影中的一样。从前面的计算已经知道16：9屏幕的纵横比为1.778 。由此可知长度为7.112 。

由此可以根据已知的Near、Far、Size、Aspect的值来确定正交投影的裁剪矩阵。

可以根据如上公式实际计算一下当前的摄像机的裁剪矩阵：

用刚刚求出的矩阵来对A点进行变换可以得出A点在裁剪空间中的坐标。

可以发现，在变换完之后，A点的w分量还是1，不像是透视投影的计算结果中w分量变成了别的值。但是不变的是判断顶点是否被裁剪的公式，依然和透视投影一样。

五、屏幕空间

这一步就到了对一个顶点进行变换的最后一步，求出顶点在屏幕上的最终位置，也就是把视锥体投影到屏幕空间。

屏幕空间是一个二维空间，所以我们需要把顶点用齐次除法（homogeneous division）也叫透视除法（perspective division）来把顶点从裁剪空间投影到屏幕空间中。

齐次除法就是就是用齐次坐标系的w分量去除以x、y、z分量。裁剪空间在经过齐次除法之后，会变换到一个立方体内。

上图中上半部分是透视投影裁剪空间的变换，下面是正交投影裁剪空间的变换，可以看到，经过齐次除法之后，两者都变换为了x、y、z都在-1到1区间的正方体内。

但是现在我们得到的还是一个三维空间的坐标，接下来就要进行屏幕映射。屏幕空间是一个二维空间，OpenGL中规定的屏幕空间是以屏幕左下角为原点（0，0），屏幕右上角为（1，1）。

齐次除法和屏幕映射一般会合并计算，其公式如下：

在上面的公式中screen x和screen y分别代表屏幕上的像素坐标，clip x和clip y和clip w分别代表顶点在裁剪空间中的x和y以及w分量，pixelWidth和pixelHeight分别代表屏幕的像素分辨率。

上面的式子中没有提到z分量的作用，z分量在这个步骤中的作用只是被记录，等待某些特殊的shader读取这个信息搞一些骚操作。

在上一步的计算中我们得到了A点在正交投影的裁剪空间中的坐标（-0.524， 0.365， -0.702， 1）和B点在透视投影的裁剪空间中的坐标（-0.281， 0.75， 1.75， 2.348）。假设我们的屏幕分辨率为1920*1080，接下来就计算一下正交摄影机中的A点和透视摄影机中的B点最终在屏幕上的像素位置。

最终A点的坐标为（456.96， 737.1） ， B点的坐标为（845.111 ， 712.487） 。如下，我们可以在摄像机视图中看到这两个点的坐标是否和直觉相同。

六、总结

到这里就是把一个顶点从模型空间变换到屏幕空间中的全部计算过程。通常在一个shader几何阶段的计算当中还有很多其他的操作，上面学习的只是一个最基本的变换。

顶点着色器的最基本的任务就是把顶点坐标从模型空间转换到裁剪空间中，在这个基本操作之外，还有很多的特殊效果可以靠编程人员的聪明才智来实现。