计算物理基础:第十章-物理综合应用习题
参考北京师范大学的《计算物理基础》
第十章-物理综合应用习题
1.单摆的混沌运动
本节介绍,有驱动力,有阻尼的单摆运动所产生的混沌运动和周期分叉运动。
- 没有驱动力,没有阻尼的单摆方程: \frac{d^2\theta}{dt^2}+sin\theta=0
- 有驱动力,有阻尼的单摆方程: \frac{d^2\theta}{dt^2}+2\beta\frac{d\theta}{dt}+sin\theta=fcos\omega t
阻尼与速度成正比,原频率为 \omega ,振幅为 f ,计算时,通常取 \beta=\frac{1}{4},\omega=\frac{3}{2}
如果给出合适的驱动力和初始条件,以上方程会出现周期分叉现象,周期运动。混沌运动。为了能观察这种复杂的现象,我们要学会做 庞加莱截面 。
(1)庞加莱截面的思想:
对于方程 \frac{d^2\theta}{dt^2}+2\beta\frac{d\theta}{dt}+sin\theta=fcos\omega t ,引入 \varphi=\omega t ,得到一阶三元微分方程组:
\frac{d\theta}{dt}=p\\ \frac{dp}{dt}=-2\beta\frac{d\theta}{dt}-sin\theta+fcos\varphi\\ \frac{d\varphi}{dt}=\omega
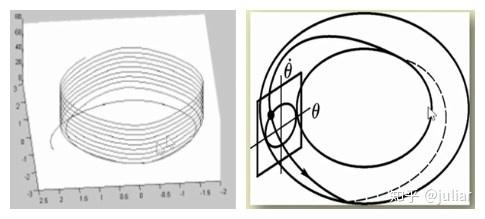
由相角 \varphi 的周期性,将上面图进行压缩,就可以得到一个类似轮胎面的形状图。 \theta 和 p 产生的轨线相当于在一个轮胎面上做环绕,若 \theta 和 p 的运动非常复杂,放在平面上看,轨线就会缠绕在一起。立体地,在轮胎面上做截面,截面上的 \theta 和 p 的图形若穿过截面,就会在截面上留下一个点,若在不同的周期穿过的位置不同。

(2)庞加莱截面的应用:
- 极限环吸引子:给定不同的初始条件,得到不同的极限环形式
当驱动力较小,如 f=0.8 ,从不同的初始条件出发,经过长时间运动最终都落到同一个椭圆上。
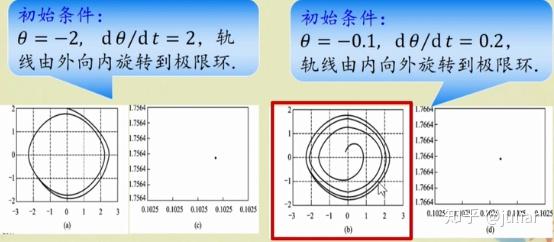
- 对称性破缺
当 f=1.03 ,从不同的初始条件出发,得到不同的蛋形的吸引子,它们左右反射对称,原来的左右对称性被破坏。(上下分别是:相图、庞加莱截面图)
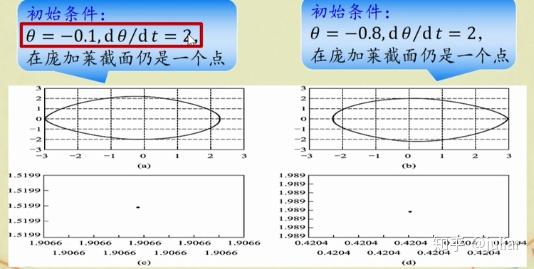
- 倍周期分叉与混沌
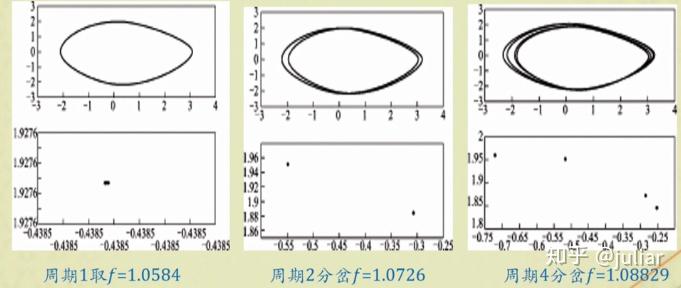
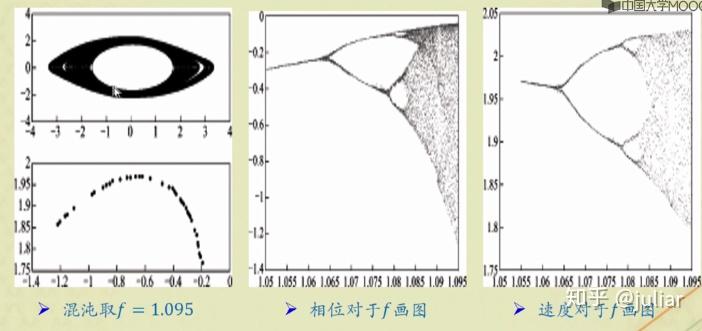
matlab实现相图和庞加莱截面图:
function
jscx69
u=2/3;a=0.5;ZQ=3*pi;%初始条件 ZQ:周期
%f=1.0584;%周期1
f=1.0726;%对应周期2的驱动力
%f=1.0891;%周期4,
%f=1.095;%混沌
[T,Y]=ode45(@dby,[0:ZQ/100:30*ZQ],[-0.8,2]);%解方程 在一个周期ZQ中取100个点
figure
subplot(2,1,1)%画相图
plot(Y(2500:end,1),Y(2500:end,2))
subplot(2,1,2)%画庞加菜截面图
xx=[];yy=[];
for j=2500:100:3000
xx=[xx,Y(j,1)];
yy=[yy,Y(j,2)];%每个周期取一点
plot(xx,yy,'or')
axis([-0.7 -0.2 1.8 2.0])
function ydot=dby(t,y) %单摆方程
ydot=[y(2);-sin(y(1))-a*y(2)+f*cos(u*t)];
end得到在周期为2的驱动力下的相图和庞加莱截面图如下:(也可以通过取不同的f,得到其他周期的图)
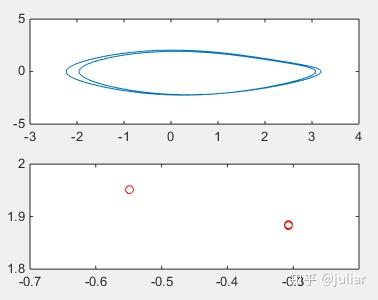
分叉图
function jscx70 %分岔图约19秒
figure
u=2/3;a=0.5;ZQ=3*pi;ff=1.06:0.00006:1.09;
FF=[];YY=[];
for k=1:length(ff)
f=ff(k);
[T,Y]=ode23(@dby,[0:ZQ/30:20*ZQ],[-0.8,2]);
FF=[FF,f];
YY=[YY;Y(501:30:end,2)'];
plot(FF,YY,'r*','markersize',2)
drawnow
function ydot=dby(t,y)
ydot=[y(2);-sin(y(1))-a*y(2)+f*cos(u*t)];
end
可见,随着ff的变化,周期为1、周期为2、周期为4,直至出现混沌。
2.倒摆实验与描述倒摆实验的杜芬方程(Duffing)
杜芬方程: \frac{d^2x}{dt^2}+x^3-x+\delta\frac{dx}{dt}=\gamma cos(\omega t)
倒摆的运动方程

将其进行简化标兵进行无量纲化,即可得到杜芬振动方程 \frac{d^2x}{dt^2}+x^3-x+k\frac{dx}{dt}=f cos\omega t ,阻尼项 k\frac{dx}{dt} 会消耗能量,驱动项 f cos\omega t 补充能量,最终方程的解有周期解或混沌解。
k=1.5 时,出现周期为1的情况,且吸引子是一个点,在频谱图上是一个频率
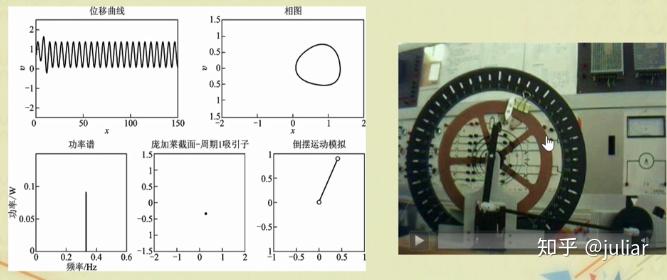
k=1.35 时,出现周期为2的情况,且吸引子是两个点,在频谱图上是两个频率
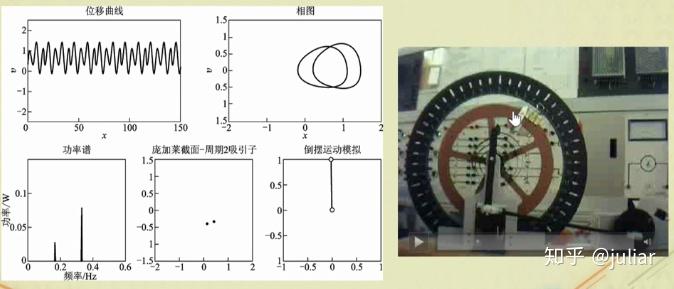
k=1.15 时,出现混沌解,在相图上画出奇怪吸引子,它的频谱是连续的。
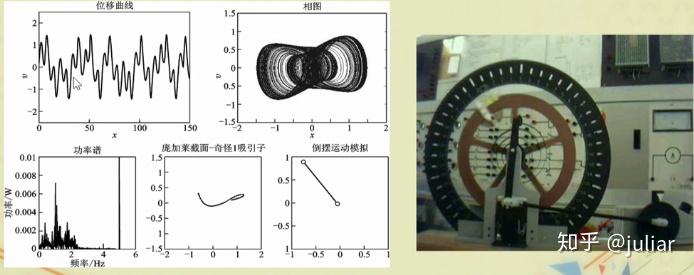
matlab演示:
function jscx70 %分岔图约19秒
figure
x0=0.1;v0=0.1;d0=0.5:0.005:1.5;
axis([0.5 1.5 -1.5 1.5])
hold on
for k=1:length(d0)
d=d0(k);
[t,u]=ode45(@dbfun,[0:2*pi/60:60*pi],[x0,v0]);
plot(d,u(901:60:1800,2),'r.')
drawnow
function ydot=dbfun(t,y)
r=1;w=1;
ydot=[y(2);-y(1)
^3+y(1)-d*y(2)+r*cos(w*t)];
end
位移图
function jscx72 %分岔图约19秒
global d
x0=0.1;v0=0.1;d0=0.78;
[t,u]=ode45(@dbfun,[0:0.01:100],[x0,v0]);
[t1,u1]=ode45(@dbfun,[0:0.01:100],[x0,v0-0.001]);
figure
plot(t,u(:,1),'r',t1,u1(:,1),'g')
xlabel('%时间');
ylabel('%摆角');
title('%混沌状态下初条件有微小差异会形成的两条分开的曲线');
%当d=1.5,为周期1吸引子;当d=1.35为周期2吸引子;当d=1.15为奇怪吸引子,
%读者可以改变d值,以观察不同的情况
d0=[1.5,1.35,1.15];
str{1}='%庞加莱截面一周期1吸引子';
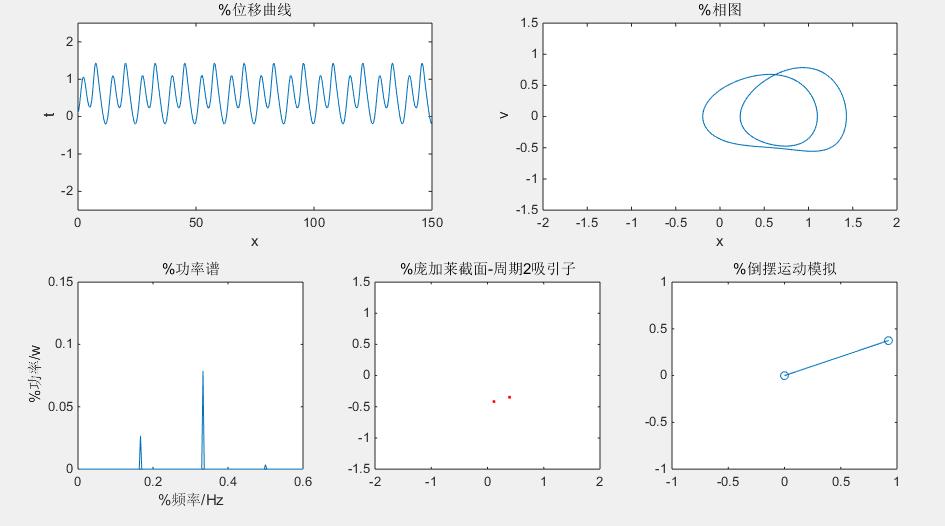
str{2}='%庞加莱截面-周期2吸引子';
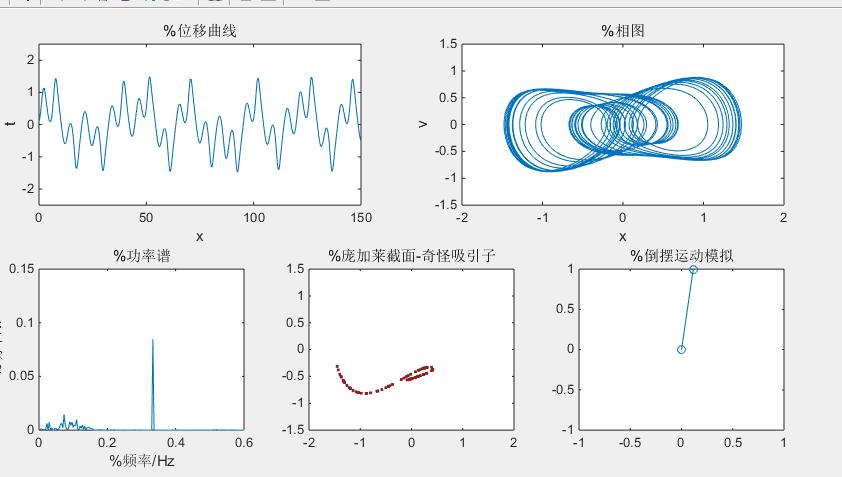
str{3}='%庞加莱截面-奇怪吸引子';
for j=1:3
d=d0(j);
[t,u]=ode45(@dbfun,[0:2*pi/300:200*pi],[x0,v0]);
figure
set(gcf,'unit','normalized','Position',[0.04 0.04 0.94 0.8]);
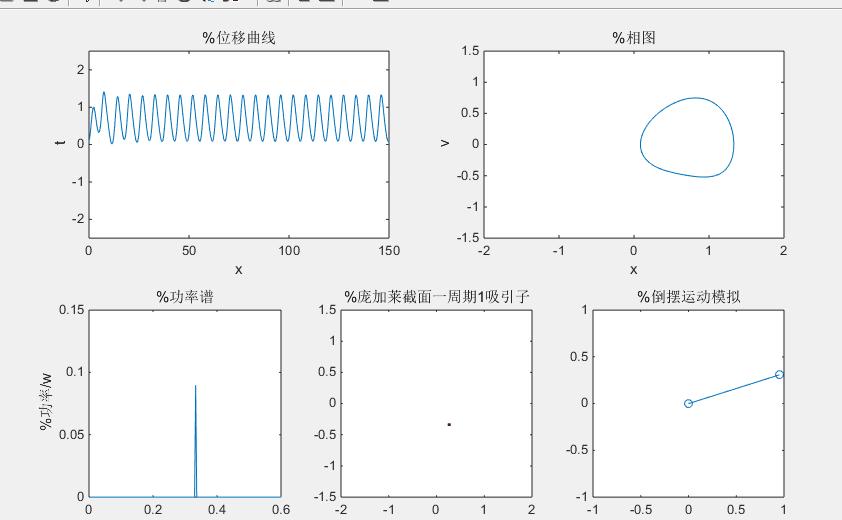
subplot(2,2,1)%位移曲线
plot(t,u(:,1))
title('%位移曲线');
axis([0,150,-2.5,2.5]);
xlabel('x');
ylabel('t');
subplot(2,2,2) %相图(奇怪吸引子)
plot(u(20000:end,1),u(20000:end,2))
title('%相图');
axis([-2 2 -1.5 1.5])
xlabel('x');ylabel('v');
Y=fft(u(:,1));
Y(1)=[];n=length(Y);m=fix(n/2);
power=abs(Y(1:m)).^2/n^2; %功率
freq=100*(1:n/2)./n; %频率
subplot(2,3,4)
plot(freq,power)
axis([0 0.6 0 0.15])
title('%功率谱');
xlabel('%频率/Hz'); ylabel('%功率/w');
subplot(2,3,5)%庞加莱截面
plot(u(2000:300:30000,1),u(2000:300:30000,2),'r.');
axis([-2 2 -1.5 1.5])
title(str{j});
subplot(2,3,6)
h=plot([0,sin(x0)],[0,cos(x0)],'o-','erasemode','xor');
%h=animatedline();
axis([-1 1 -1 1])
title('%倒摆运动模拟');
for i=25000:30000
set(h,'xData',[0,sin(u(i,1))],'yData',[0,cos(u(i,1))]);
drawnow
function ydot=dbfun(t,y)
r=1;w=1;
ydot=[y(2);-y(1)^3+y(1)-d*y(2)+r*cos(w*t)];
%输出有点小问题,还没有改好
警告: EraseMode 属性不再受支持,而且在以后的版本中会出错。请使用 ANIMATEDLINE 函数来生成线和点动画,而不是 EraseMode 'none'。删除设置为
'normal'、'xor' 和 'background' 的 EraseMode 实例的影响极小。
> In jscx70 at 55
警告: EraseMode 属性不再受支持,而且在以后的版本中会出错。请使用 ANIMATEDLINE 函数来生成线和点动画,而不是 EraseMode 'none'。删除设置为
'normal'、'xor' 和 'background' 的 EraseMode 实例的影响极小。
> In jscx70 at 55
错误使用 matlab.graphics.chart.primitive.Line/set
对象无效或已删除。
出错 jscx70 (line 60)
set(h,'xData',[0,sin(u(i,1))],'yData',[0,cos(u(i,1))]);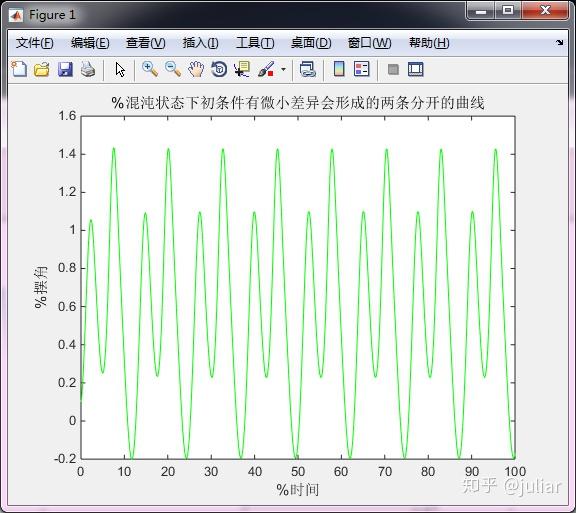
3.自激振动与范德波耳方程
强迫范德波耳(VDP)方程
描述有外驱动力的非线性有阻尼的自激振动系统: \mu :小的正常量,x_{0}:常数,V:外驱动力的振幅, \omega :角频率
\frac{d^2x}{dt^2}-\mu(x_{0}^2-x^2)\frac{dx}{dt}+\omega_{0}^2x+Vcos\omega t=0
上述方程也自激振动方程,是一个非线性有阻尼的振动方程,通过反馈补充阻尼损耗的能量,产生稳定的周期运动。它如何实现阻尼的消耗呢?

产生稳定的周期运动(极限环)时,相轨线趋于同一闭环曲线(极限环):
极限环外的相轨道向里盘旋;
极限环内的相轨道向外盘旋;
VPD方程通向混沌的道路:
令 y1=x,y2=dx/dt ,则强迫VDP方程可化为
\frac{dy_{1}}{dt}=y_2\\ \frac{dy_{2}}{dt}=\mu(x_{0}^2-y_{1}^2)y_{2}-\omega_{0}^2y_{1}-Vcos\omega t
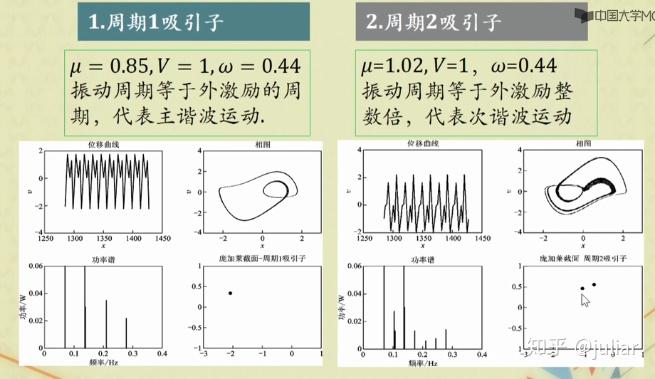
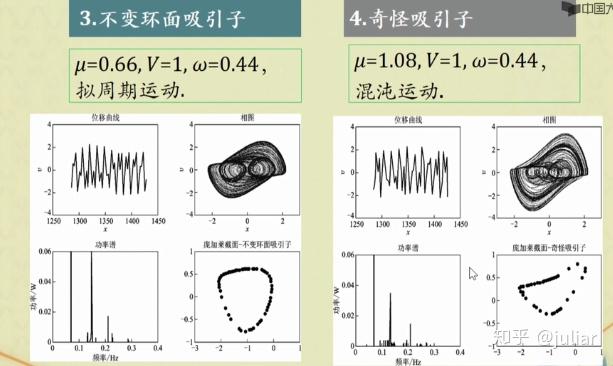
取 x_{0}^2=1,\omega_{0}^2=1 ,作计算并画出位移图、相图、频谱图、庞加莱截面图。
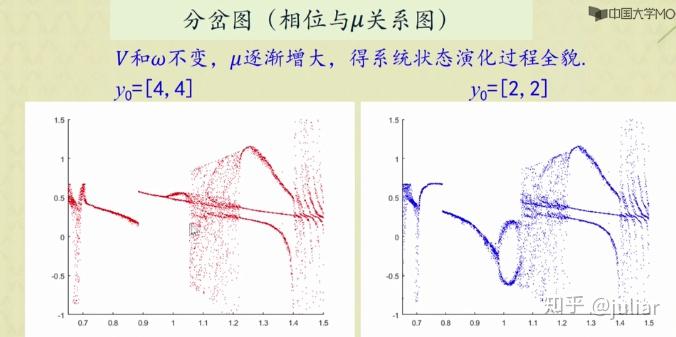
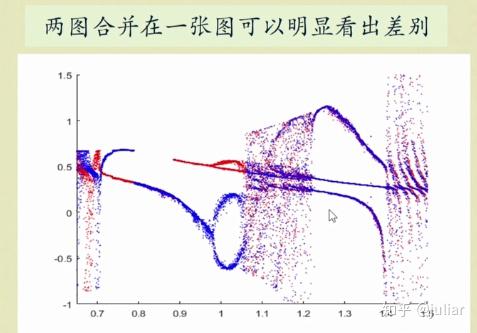
function jscx73%zjzd
global uu w v
u=[0.85,1.03,0.6,1.0732];
w=0.44; T=2*pi/w; v=1;
str{1}='%庞加莱截面一周期1吸引子';
str{2}='%庞加莱截面一周期2吸子引子';
str{3}='%庞加莱截面一不变环面吸引子';
str{4}='%庞加莱截面一奇怪吸引子';
for j=1:4
figure
uu=u(j);
[t,y]=ode45(@vdpfun,[0:T/1000:100*T],[4,4]);
subplot(2,2,1)
plot(t(90000:end),y(90000:end,1));
title('%位移曲线');
xlabel('x'); ylabel('v');
subplot(2,2,2)
plot(y(3000:end,1),y(3000:end,2));
title('%相图');
xlabel('x'); ylabel('v');
subplot(2,2,3)
Y=fft(y(:,1)); %傅里叶分析
Y(1)=0; n=length(Y); m=fix(n/2);
power=abs(Y(1:m)).^2/n^2;
dt=t(2)-t(1);
freq=1/dt*(1:n/2)./n;
plot(freq,power);
axis([0 0.4 0 0.06])
hold on
title('%功率谱');
xlabel('%频率/Hz'); ylabel('%功率/w');
subplot(2,2,4)
axis([-3 1 -1 1])
hold on
for i=5000:1000:100000
plot(y(i,1),y(i,2),'r.');
end;
title(str{j});
