通过对原始数据进行一系列变换和处理,生成新的训练样本,从而扩充数据集的大小和
UDA(Unsupervised Domain Adaptation):
解决在源域和目标域之间存在分布差异时的分类或回归问题。其目标是仅利用未标记源域数据和目标域数据来构建一个具有良好泛化能力的模型,以适应目标域的分布。其核心思想时通过学习源域和目标域之间的共享特征或对齐它们的表示空间,以便在目标域上具有较好的性能。
DDAR:
《 iDAG: Invariant DAG Searching for Domain Generalization 》
背景知识:
经验风险最小化(Empirical Risk Minimization, ERM)
问题框架,用来构建和训练模型以及最小化在训练数据集上的损失函数。
目标是通过最小化训练数据上的经验风险来选择和调整模型的参数,以期望在未见数据上获得良好的性能
由于ERM框架存在过拟合风险(倾向于在训练数据上获得零错误),故此通常引入正则化以限制参数的复杂性(通过引入正则化项,模型在优化过程中会综合考虑损失函数和正则化项,从而在平衡拟合训练数据和控制参数复杂性之间找到合适的权衡。正则项的存在使得模型倾向于选择更简单的参数配置,有助于提高模型的泛化能力,减少过拟合的风险)。
Invariant factors :不变量因素
Domain-specific factors: 特定领域因素
Spurious factors: 误差因素
Diversity shift:“差异转移”,即某些判别特征在训练域中出现过,但测试域中可能消失
Correlation shift: 相关移位(相关转变),会诱发虚假的预测特征,例如在训练过程中,图像的背景会主导分类结果
iDAG:
zy:不变特征
zse: 更易拟合的虚假特征
zre: 域私有特征
为了进行因果发现,iDAG框架需要处理潜在因素联合集和标签之间的因果关系
包括两个关键部分,
特征,用于更新特定领域的原型;然后,将原型与标签连接起来,用于优化有向无环图。DAG上的绿色阴影表示因素对标签y的总体影响,与这些因素相对应的不变特征用于最终预测。
featurizer: 功能
classifier: 分类器
updata prototypes: 更新数据原型
feature space: 特征空间
construct factors: 构建因子
prototype label:原型标签
total effect mask:总效果掩码
和所有的图的共同结构相匹配,则丢弃从领域私有因素
开始的的有向边,并将
的关联识别为一个正确的因果方向。
:通过观察数据或领域知识可以确定vc-->vi或vj-->vi的一个方向作为正确的因果关系。
Searching DAG from Features and Labels
为了学习不变的DAG,最简单的想法是每个领域学习DAG,然后提取它们的共享子图。但是相同的数据可能导致多个有效的DAG,它们是满足相同条件独立性关系的一组图形,因此在这种情况下提取子图可能会很困难。所有我们通过对解释所有领域中因果关系的单个领域不变图进行惩罚来解决这个问题。
简单来说,在学习不变的DAG时,针对每个领域学习一个DAG可能会导致不同的DAG之间存在一些差异,因为相同的数据可以对应多个满足相同条件独立性关系的DAG。为了解决这个问题,iDAG方法通过对单个领域不变图进行惩罚,推动学习一个能够解释所有领域中因果关系的共享子图。这样可以确保学习到的DAG具有一致的因果结构,能够在跨领域的情况下进行泛化。
在每个训练步骤中,我们希望从当前学习到的特征和标签中搜索一个由可学习邻接矩阵A ∈ R^(d+1)×(d+1) 表示的不变DAG,
具体重构过程:对于每个因子,我们首先采用行向量Ai来屏蔽非父节点元素,然后通过函数gi将父节点映射到第i个因子
对于数值型节点 v
i
函数 gi 将邻接矩阵和向量因子v相乘,用它们俩的乘积来映射父节点的第i个因子。(可以映射的原因:在数值型因子的条件下,可以直接使用线性映射来建立因果关系。邻接矩阵表示了父节点与第i个因子之间的连接关系,因子向量v包含了所有的因子值。A与v相乘可以将父节点的值传递到第i个因子。这种线性映射的使用是因为数值型因子在表示上是连续的,并且可以
通过简单的数学运算来进行建模,通过乘积运算,将父结点的值与相应的权重相乘,从而得到第i个因子的值
)
对于分类型因子 vi
函数 gi 将邻接矩阵A转置然后与因子向量v的元素逐元素相乘,然后通过权重矩阵W进行映射。A表示将父节点分配给子节点的指示矩阵,W是一个权重矩阵,将父节点映射到分类问题的类别logits,这是为了特别适用于分类任务。(再分类型因子的情况下,v代表了一个离散的类别或标签,A的转置表示了父节点与第i个因子之间的连接关系。通过将A的转置与v的元素逐元素相乘,可以选择性的将父节点的信息传递给第i个因子。如果A的转置中的某元素为非零值,表示父节点与第i个银子之间存在连接关系。,那么相应位置的因子v的值将被保留,而其他位置上的值将被置为0。通过此选择性地传递与父节点相关的信息,并将其与权重矩阵W进行映射。通过权重矩阵W的映射,我们可以将传递给第i个因子的父节点的信息转换为分类问题中的类别logits(对数概率)。权重矩阵W的作用是将父节点的信息映射为适用于分类任务的表示形式,以便在后续的分类模型中进行处理。)
然后,根据上述公式得总体损失函数:
公式解释:
对于重构误差项,计算每个瓶颈特征元素zi,与其对应的函数gi的输出之间的L2范数(欧氏距离),并将所有瓶颈元素的重构误差累加求和(L2范数衡量了重构特征和真实特征之间的距离);对于分类损失项,针对分类标签变量,使用交叉熵损失函数,gy表示函数关于瓶颈特征向量的输出,y是分类标签的真实值
上式为完整的图重构损失函数,用于计算完整的图重构损失。这个损失函数的目标是通过最小化重构误差和分类损失来训练模型以实现图结构的重构。
重构误差
通过计算瓶颈特征元素和其对应的函数gi的输出之间的L2范数来度量,重构误差项确保了模型生成的图结构能准确地重构原始数据的特征;
分类损失
通过计算分类标签和gy输出之间的交叉熵损失来度量,分类损失项鼓励模型在分类问题上具有准确的预测能力。
通过最小化完整的图重构损失,模型可以学习到适当的图结构以及如何将输入特征映射到瓶颈特征元素和分类标签上,这有助于实现数据的生成。
上一个损失函数不能保证图是无环的,当存在更容易拟合的虚假关系时,最小目标二乘函数往往会引入估计图中的循环,为了消除虚假关系,引入指数迹约束保证A的无环属性。
公式符号解释:
A表示邻接矩阵,
表示逐元素相乘,Tr表示矩阵的迹(即对角线元素之和),d表示矩阵的维度
指数迹约束的目的是限制邻接矩阵的指数迹,从而保证所估计得图是无环的。即,通过将邻接矩阵的逐元素平方作为指数矩阵的指数,可以计算矩阵的指数迹,并减去(d+1)的值(对于一个有向无环图的邻接矩阵,指数迹的求和结果为d个1的和,将指数迹的值减去(d+1)是为了与无环图进行区分,去报在指数迹为零时,得到的是一个有向无环图)。如果指数迹的结果等于零,那么邻接矩阵满足无环性质(因为有向无环图的邻接矩阵中对角线元素的值通常为零),即使一个有向无环图。
该公式目的是限制一个节点在这个有向图中无论经过多少步都不能到达自身。
符号解释:vec:将矩阵向量化,
用于强制DAG的稀疏性的权重参数,
:对应重构损失
公式的图学习目标由两部分组成,第一部分是重构损失
,用于度量模型生成的图与原始数据之间的差异,这个损失函数可以根据具体情况使用不同的距离函数来度量重构的准确性。第二部分是L1正则化
,通过对邻接矩阵进行L1正则化,促使邻接矩阵具有稀疏性(通过对A进行L1范数惩罚,使得邻接矩阵中的大部分元素趋向于零,使得途中只有少数重要的因果关系被保留,减少无关或虚假关系的影响,
的hi用于控制L1正则化强度的权重系数),有助于提取重要的因果关系,减少虚假关系的影响。约束条件确保了估计的邻接矩阵满足无环性质即估计的图示一个有向无环图。
综合而言,通过优化这个损失函数,我们可以同时实现准确的图重构、稀疏的邻接矩阵以及无环性质的约束,从而推断出正确的因果方向,并减轻相关性偏移的影响。
通过上述式子,进一步深入思考,返回最初的问题对于虚假特征Zse,学习的顺序是ye-->Zse,因为存在相互独立的噪声
,从原因到结果的关系更容易学习,而五环越俗完全排除了反向边缘的存在;对于不变特征Zy,学习的顺序是Zy-->ye,这种关系更容易被学习到;对于领域私有特征,他们与其他因素之间的关系较少,因此不会被发配边缘
当环境数量为E时,并且满足定理一是,根据定理二,如果
,则至少有
的概率满足
与新的特征向量
进行加权平均来得到新的原型向量。具体地,新的原型向量是当前原型向量乘以 \gamma 的值,再加上新的特征向量乘以 (1-\gamma) 的值。最后,通过对新的原型向量进行归一化操作(Normalize)来保证原型向量的单位长度。
这种移动平均的更新过程使得原型向量在训练过程中相对稳定。通过保留历史的原型信息,每次更新都考虑了当前特征向量和以往特征向量的权衡,从而更好地适应数据的变化。这种稳定的原型更新过程也有助于保持因果图的稳定计算。
总而言之,该公式描述了通过滑动平均方式更新原型向量的过程,以提高模型训练的稳定性和因果图的可靠性
提取稳定预测的不变特征:
为提取稳定预测的不变特征,基于直接因果关系父节点
预测y,由于普通
(特征)通常受到噪声影响,当仅基于父节点进行预测时,预测可能过于敏感,为了获得更稳定的预测,需收集y的直接因果因素及DAG中的祖先因素。因此,通过包括所有直接和间接因素来定义不变特征。根据矩阵A的第 (i, j) 元素的 k 次方的正值表示存在长度为 k 的路径 vi → · · · → vj 的思想,我们推导出
以类比于有向的成对总效应,即上式。
,为矩阵,,该矩阵用于表示变量之间的总因果效应。A是表示英国关系的邻接矩阵,其中Aij表示从变量vi到vj的因果关系强度;(A⊙A) 表示 A 与自身的逐元素相乘运算,得到的矩阵表示 A 中变量之间的二阶因果关系;
对k阶因果关系进行求和,
表示对矩阵
进行指数运算,其中指数函数用泰勒级数站靠进行近似计算。
包含了变量vi到vj的所有直接和间接因果效应的关系,对于提取稳定预测中的不变特征具有重要意义。
:类比于从vi到vj的总因果效应,然后不变特征ze
包含了y的所有直接和间接因果特征
不变特征优化稳定分类器,损失函数即上式。
:训练数据集,
:交叉熵损失函数(用于衡量预测值和真实标签之间的差异),
:稳定分类器的预测值,
:从输入样本x提取的特征。通过期望操作(对所有样本的损失进行平均),计算模型在训练数据集上的损失函数
表示不变特征矩阵
的转置的子矩阵,其中包含了所有直接和间接因果特征。y:真实的标签
该公式通过将输入样本提取的特征与不变特征进行逐元素的相乘,并将结果输入稳定分类器进行预测,然后将预测结果与真实标签进行比较得到损失值。该损失函数用于优化稳定分类器,使其能准确地预测基于不变特征的目标函数。
(内积)计算。
将锚点样本与正样本原型的相似度除以锚点样本与完整样本集合中所有元素的相似度之和,对上述结果取指数函数,并除以温度参数 τ 进行缩放。指数函数的作用是增强相似度之间的差异,最后,对取指数函数后的结果取对数,然后取负值作为对比损失的值。
总体来说,这个目标函数通过比较锚样本与正样本原型的相似度与锚点样本与其他样本或原型的相似度之间的差异,来衡量锚点样本预期正样本原型的关系。通过最小化对比损失,我们可以使锚样本更接近其正样本原型,并远离其他样本和原型2,这样能够提高原型的代表性,并在模型训练中实现更好的分类性能
域内原型对比学习(PCL)
-
构建领域内嵌入池:
a. 收集每个样本的特征和每个领域的原型。
b. 构建领域内嵌入池
包括两个部分,
,所有环境e和类别c的原型
是当前小批量B中的特定领域特征
-
定义正样本集合
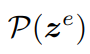
。
a. 对于给定的样本
,定义正样本集合;
b. 它包括与
相同的环境e’和类别c‘的
中的原型k’
-
计算领域内对比损失
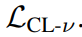
域间PCL
为实现通过在共享空间中对齐样本的不变因素来学习一个不变得有向无环图,开发了一种新的PCL损失函数
-
不变特征提取,使用总效果效应,提取每个样本的不变特征。这个过程中有助于识别在不同领域中保持一致的因素
-
跨领域嵌入池,通过结合两个组成部分构架跨领域嵌入池
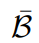
。
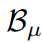
,包含所有类别的原型,记为
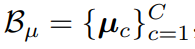
,这些原型代表了在不同领域中同一类样本共享的共同特征。
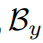
,包含当前小批次的不变特征,表示为
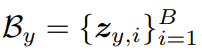
,这些特征捕捉了在共享空间中样本的不变因素
-
正样本集合定义,
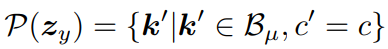
-
计算跨领域对比损失,

通过将A的转置与v的元素逐元素相乘,可以选择性的将父节点的信息传递给第i个因子。即,通过将邻接矩阵的逐元素平方作为指数矩阵的指数,可以计算矩阵的指数迹,并减去(d+1)的值(对于一个有向无环图的邻接矩阵,指数迹的求和结果为d个1的和,将指数迹的值减去(d+1)是为了与无环图进行区分,去报在指数迹为零时,得到的是一个有向无环图)。对于重构误差项,计算每个瓶颈特征元素zi,与其对应的函数gi的输出之间的L2范数(欧氏距离),并将所有瓶颈元素的重构误差累加求和(L2范数衡量了重构特征和真实特征之间的距离);