Invariant Information Bottleneck for Domain Generalization.(N,AAAI 2022)
翻译题目:不变的信息瓶颈对领域泛化。
视频记录:
领域泛化:1.生成更多数据 2.Represeentation learning 3.集成学习 4.meta learning 提取更本质的信息
IRM第一个公式,每个domain的risk(相当于loss)加起来最小,第二个公式,一致最小(50+50优于0+100),下面那个IRMv1就是提出了一个practice的形式,用拉格朗日的逼近方式逐渐优化。

用互信息的方式表示IRM,X-input data,y-label,D-domain label,φ-encoder,Z=φ(x)是提取特征的表示,左边的第一项表示表示提取的feature Z 应该尽量包含true label的信息,让整个式子尽量大就是 让第二项尽量小,第二项(if correctly condition on feature Z,label Y should be as less related with domain D),解释是比如下图是art和cartoon的狗,如果是根据颜色判别狗,则有很多五官的颜色,如果是根据shape判别狗,就是相关的。(D和Y之间的联系信息不可以从φ(x)中获得)(Q)。
我的理解就是也是获得一些不同domain相通的信息,舍弃特有的信息。


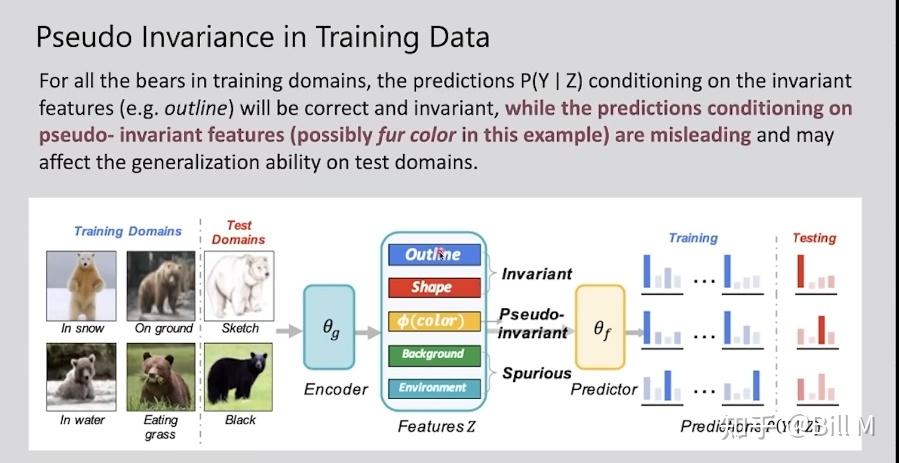
假设有6个domain,4个训练,2个测试,encoder后的outline和shape都是一致的,但是color是不一样的,训 练的时候偏棕色,但是测试的时候有的熊没有颜色了 。pseudo-invariant feature 伪不变特征。可以看出这个pseudo-invariant的来源是由于它用的feature太多了,那我们减少它用的feature会不会就好转了。
希望我们的z包含conditional invariance(条件不变)信息的同时,还希望z包含尽量少的关于x的信息。我们这里没有decoder,我们这里是一个分类层。
IB 简单一句话来讲就是它希望它的feature z被encoder后,服从一个多元高斯分布,服从多元高斯分布后它就能满足尽量的分离,尽量地无关,然后降维把最关键的信息保留下来。
我们的目标就是通过IB后优化feature,但是现在的方法没有很好的办法衡量通过IB后能不能很好地分辨出高维特征是outline还是shape什么的。

为什么IB就能把outline和shape选出来呢?而不是color什么的
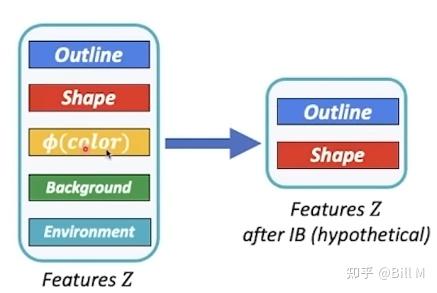
从disentangled representation(解耦合)的角度来看,其中最出名的参考论文beta-VAE,
outline和shape都是预测熊的,color有时候一样有时候不一样,就会导致不同的degrees of disentanglement不一样,color这个分量会在IB这个结构里liminate掉。
很直观。
我们在原有的IRM基础上把它写成了互信息的形式,在结合IB的互信息的形式,把IRM和IB写到一起,
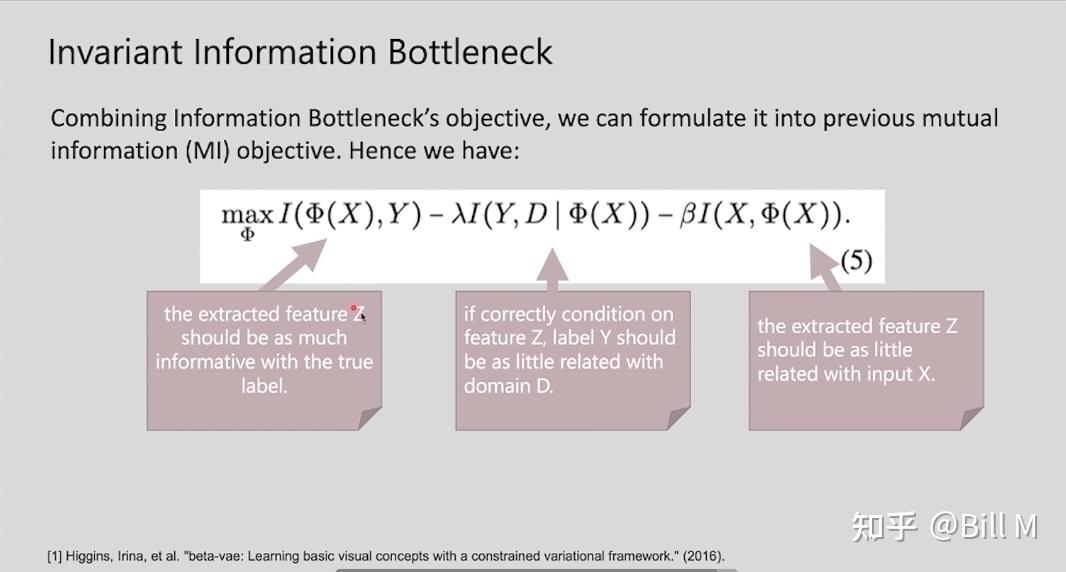
第一项是提取出的特征Z需要拥有真正label的所有信息。第二项是如果特征 Z 的条件正确,标签 Y 应该与domain D 的相关性尽可能小(这个意思就是你的Z尽量condition在一个正确的上面,比如说shape,outline,这样你是熊这件事情就和它来自于哪个domain无关了)。第三项是被提取的特征Z应该和输入X相关性比较小(还有多了就会出现pseudo-invariant现象)。
变分近似法求解:
r(z)去近似p(z),q(y|z)去近似p(y|z),同时让p(z|x)成为随机编码器。这里就是把MI(互信息)的目标写成变分的形式。(包括variational information bottleneck这篇论文也有推导)

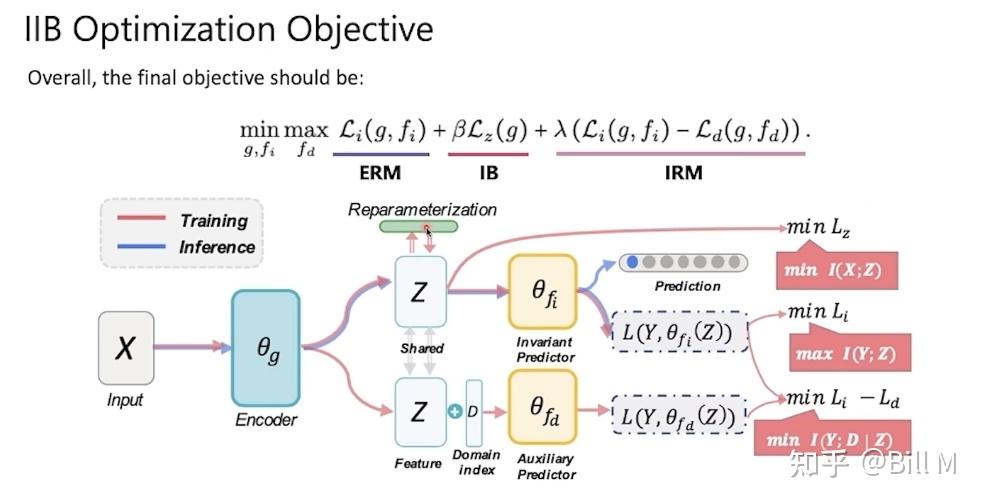
Reparameterization 再参数化,Invariant Predictor不变预测器,Auxiliary Predictor辅助预测器
X经过encoder,拿到z,要做一个IB里面的reparameterization之后再去做KL。
创新性是什么?

怎么优化IRM,分析出的缺陷有pseudo-invariance 和 geometric-skews。
引入了IB这个结构到IRM里面。
写到了一起,然后再用变分的方式去实现。

摘要:
领域泛化的主要挑战是克服多个训练域和不可见测试域之间的潜在分布转移,一种流行的DG算法旨在学习跨训练域具有不变因果关系的表示,然而,某些特征,称为伪不变特征 pseudo-invariant features,可能在训练域是不变的,但在测试域不是,并会大大降低现有算法的性能。为了解决这个问题,我们提出了一种新的算法,称为 Invariant Information Bottleneck(不变的信息瓶颈) (IIB),它学习跨training和testing域的最小充分表示。通过最小化表示和输入之间的互信息,IIB减轻了对伪不变特征的依赖,这是DG所希望的。为了验证IIB原则的有效性,我们对大型DG基准进行了广泛的实验。结果表明在两个评价指标上,IIB比不变学习基线(例如IRM)的准确度平均高出2.8%和3.8%。
1.介绍:
在大多数统计机器学习算法中,一个基本的假设是训练数据和测试数据是独立的同分布的(i.i.d.)。然而,许多真实世界的应用程序是不是这样的,并且经常在训练和测试数据之间存在分布转移偏差。在这样的情况下,经典的统计学习算法具有强泛化保证。例如:经验风险最小化empirical risks minimization(ERM)方法经常不能推广由于违反i.i.d(独立同分布)原理。
已经观察到,当一个训练过的模型呈现来自不同domain的样本时,其性能往往急剧下降,即使只有小的分布偏移[7,23,71,105]。 然而,从所有可能的分布中收集训练样本是不可行的 。因此,认识和提高非分布数据的泛化能力具有重要的现实意义。
领域泛化(DG)是一种从多个不同领域学习模型,并能很好地泛化到不可见领域的方法,近年来受到了广泛的关注,在过去的几年中,DG的进展主要来自于不变表示学习[69,36,45,115]、因果关系[7,53,106,64]、元学习[57,8,27]和特征解缠[27,46,75]等领域。特别有趣的是不变因果预测(ICP)和它的后续不变风险最小化(IRM),它通过一个理论基础的因果描述来解决DG。
ICP假设数据是根据结构因果关系生成的模型(SCM)[73]。数据生成过程的因果机制 causal mechanism在不同领域是相同的,而非因果机制 non-causal mechanisms在不同领域可能不同,该条件通过学习不变特征来揭示因果结构。
特别是,不变风险最小化(IRM)[7]试图学习一个只利用不变特征的不变分类器。ICP中的理论分析表明,这样的分类器可以跨域泛化,即使在测试时存在分布转移。
尽管IRM方法在玩具数据集上有着直观的动机和优越的性能,但最近的一项研究以经验为依据表明,这些方法只略微优于ERM[42],而造成这种差距的根本原因尚不清楚。
为了更好地理解IRM——以及更一般的不变学习方法——我们采用信息理论的视角,通过不变来识别因果关系,并将其表述为一个约束优化问题。
IRM希望寻求一种对标签提供最大信息量但对域的变化提供最小信息量的表示,然而,我们发现IRM可以学习到一类伪不变特征,这可能是IRM失败的主要原因。具体来说,伪不变特征是环境特征的转换,这样它们在训练域上是不变的,但在测试域上是变的。当训练域的数量不够大时,IRM不可避免地同时包含因果特征和伪不变特征。冗余的伪不变特征会阻止模型捕捉因果关系,并导致对测试域的错误预测。
为了解决这一问题,我们提出了一种新的DG方法,称为不变信息瓶颈(IIB)。IIB 的目标是学习跨域不变的最小充分表示,它捕获了因果关系,同时减轻了伪不变特征的影响。总之,我们的工作提供了以下贡献:
(1)我们提出了一个新的基于互信息的不变因果预测公式。我们进一步采用变分逼近的方法来发展非线性分类器的易处理损失函数。
(2)为了减轻伪不变特征 pseudo-invariant features和几何倾斜 geometric skews的影响,受信息瓶颈原理的启发,我们建议约束输入和表示之间的互信息,通过失效模式的综合实验验证了有效性(Ahuja 等人,2021;Nagarajan、Andreassen 和 Neyshabur2021),其中 IIB 显着提高了IRM。
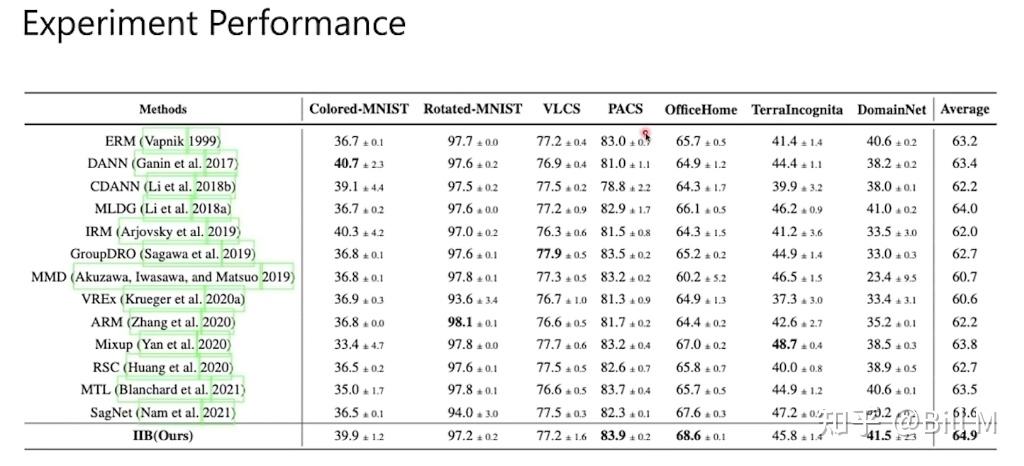
(3) 在实证方面,我们在综合基准和大规模基准上进行了大量实验,分析了eiib的性能。结果表明,IIB方法能够较好地消除伪信息,并在7个数据集上取得了0.7%的一致性改进。
2.最近研究:
Mutual Information-based Domain Adaptation 互信息域适应
领域适应是迁移学习方向的一个重要课题(Long et al. 2015;Ganin等2016;Tzeng等人2017;Long等人2018;赵等,2021,2020c,b;Li等人。2020a)。基于互信息的方法在这一领域得到了广泛的应用。关键思想是学习对标签有信息的域不变表示,可以表示为(Zhao et al. 2020a;Li等人。2020b)
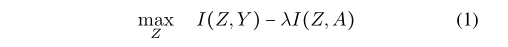
其中A是域的标识符,Z表示特征表示,Y表示标签,(1)通常采用的实现是DANN (Ganin et al. 2017)和CDANN (Long et al. 2018)。这些实现也经常被用作领域泛化的基线(Gulra- jani and Lopez-Paz 2020)。
Invariant Risk Minimization不变的风险最小化
上述方法增强了学习到的表示的不变性。另一方面,不变风险最小化(IRM)表明特征条件标签分布的不变性,具体来说,IRM寻求的是一个不变的因果预测,
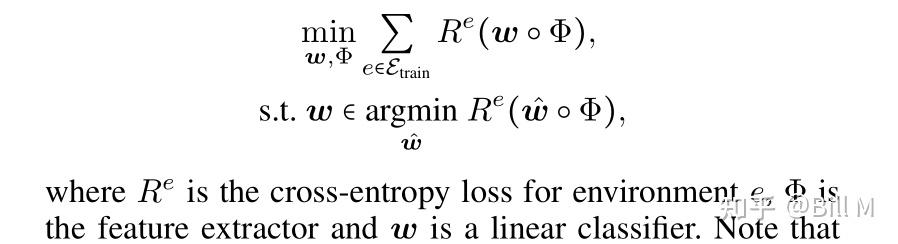
注意,上述目标是一个双层优化,难以优化。因此,(Arjovsky et al. 2019)采用一阶近似,损失函数由
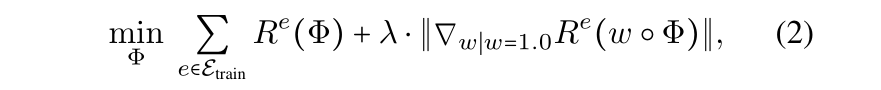
准备:
学习不变表示的失效模式Failure modes在文献中是众所周知的(Zhao et al. 2019a, 2020a)。最近,一些工作也专注于刻画IRM的失败模式(Rosenfeld, Ravikumar和Ris- teski 2020;Nagarajan, Andreassen和Neyshabur 2021年)。作为一个动机,我们首先在下面简要总结这些关于IRM的负面发现,
Pseudo-invariant Features:
即使在线性环境中,已有研究表明,原始的IRM公式(2)也不能真正恢复诱发不变因果预测的特征(Rosenfeld, Ravikumar, and Risteski 2020)。在线性情况下,一个附加的环境可以用来识别一个伪特征,如果环境的数量小于伪特征的数量,一些伪特征会泄漏到算法恢复的因果特征中,我们称之为伪不变特征。
具体地说,我们将因果特征和伪特征分别表示为zc和zs。OOD泛化可能会因为包含zs而失败,zs在测试数据集中可以是任意的。伪不变量特征的说明如图1所示。
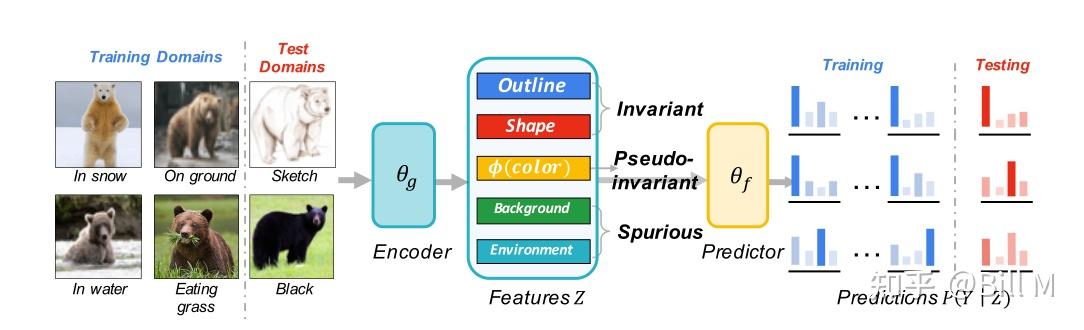
图1:OOD泛化中的特征说明。对于所有训练域中的熊,条件作用于不变特征(如轮廓)的预测P(Y∣Z)将是正确和不变的,而条件作用于伪不变特征(可能在这个例子中是毛皮颜色)的预测具有误导性,并可能影响测试域中的泛化能力。几何歪斜(Nagarajan, Andreassen和Neyshabur, 2021)是作为最大边缘分类器的捷径使用的伪特征。在本例中,ERM经验风险最小化将使用所有5个特性,因为它们为标签提供了信息。具有不变性约束的IRM将利用前3个特性。IIB,通过选择最小的充分特征,只包括形状或轮廓。
Geometric Skews 几何倾斜(Q:这块没看懂)
即使我们假设由于几何倾斜,训练数据集中的不变特征在测试数据集中也是不变的,(out-of-distribution)OOD泛化也可能失败(Nagarajan, Andreassen,和Neyshabur, 2021)。可以观察到,随着训练点数的增加, max-margin classifier的2 -范数增长。体地说,我们考虑一个不变特性zinv与一个纯特性相连接的情况zsp,
w all表示使用不变特征对所有样本进行分类的最小范数分类器,w min表示使用不变特征对样本进行分类的最小范数分类器,在S min集合中,因此,该算法可以利用虚假的特征作为捷径,对Smaj、S min进行分类,然后利用w min对剩余的S min进行分类。这种使用伪特征的分类器的范数比不变分类器小,导致OOD泛化失败。
我们提出的方法:
在本节中,我们提出了一个新的信息论目标——寻找不变因果关系,以克服信息管理目标设计中存在的两个问题。
通过互信息进行不变的因果预测
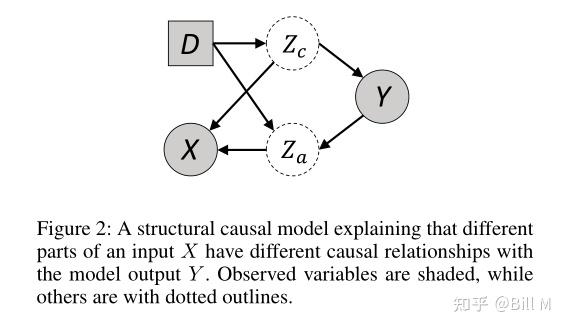
图2:一个结构因果模型,解释了输入X的不同部分与模型输出Y有不同的因果关系。观察变量用阴影表示,其他变量用虚线表示。
我们从一个结构因果模型开始,如图2所示。为了简单起见,我们省略了所有不必要的元素。一般来说,我们可以看到一个输入X可以分为两个变量,因果特征zc和环境特征za,在图2中,我们可以读出这两个特征都与Y相关,但只是zc被认为是一种因果特征。根据d-分离理念,我们认为所有数据的独立分布条件P(D,X,Y)应当满足:
(1).
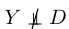
意味着Y的 边缘分布 在不同的domain中会改变。
(2).
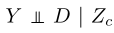
表示类标签Y在因果特征Zc的条件下独立于域D。内在的因果机制决定了其价值,Y来自于其独特的因果父zc,它不会在不同领域发生变化。
(3)
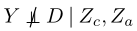
意味着条件独立性在因果特征zc和环境特征za的条件下是不成立的,因为za是D和Y之间的碰撞体。
条件独立性告诉我们,只有真正的因果关系是稳定的,并且在各主次之间保持不变。换句话说,我们应该通过寻找独立于Φ(X)与D的因果特征zc来消除伪环境特征za。Z = Φ(X)应当有以下两个优点,(1)对于相同的类标签Y, Z在不同的域之间不会改变,从而得到的条件不变性。(2) Z应该包含类label Y的信息(否则,即使是一个常量Φ(⋅)也能满足第一个目标)。以上两个条件与IRM的目标相吻合,并提出以下学习目标,其中Φ是特征提取器。
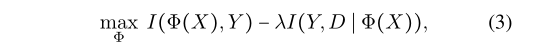
证明。请注意,I(Y,D∣Z) = 0表示Y和D依赖Φ(X)。条件独立表示P(Y∣Φ(X) = X,D) = P(Y∣Φ(X) = X),即E[Y∣Φ(X) = x],就实现了条件独立性。
IRM的失效模式
在本节中,我们首先考察了IRM的失效条件,即伪不变特征和几何倾斜。根据我们的分析,在所有满足不变因果预测约束的特征中,我们建议使用容量最小的特征,即最小的特征I(X, Z),最高的压缩比。
由于伪不变特征和几何倾斜,现有的IRM方法的失败是由于包含(变换)伪特征,我们首先给出一个例子,当特征是一维的,分类器是线性, 不变特征,伪不变特征,引起几何歪斜的特征,伪特征 ( invariant feature, pseudo-
invariant feature, feature causing geometric skews, spurious feature )如 zi, zp, zsk和zsp ,Z=[zi,zp,zsk,zsp]。在ERM模型中,所有的特征都会被采用,OOD泛化失败。我们考虑以下优化问题:
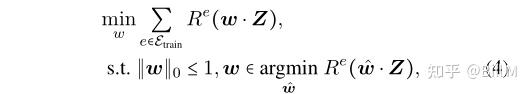
||w|| <=1是稀疏约束,上面的公式是IRM的不变风险约束,由于稀疏性约束,只有4种选择。选择zsp不能满足不变约束,而选择zp或zsk不能最小化经验风险(Q)。因此,唯一的最优解是w = [w *1, 0, 0, 0)。没有稀疏约束,优化问题变成IRM和zi, zp, zsk将被用于分类(Q)。在没有不变约束的情况下,可以选择zsp,因为包含虚假特征可以降低经验风险。
然后我们从互信息的角度将这种直觉扩展到深度神经网络的损失函数设计中。假设z1 z2是从X中提取的特征,我们有
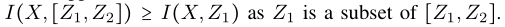
因为Z1是Z的子集。
因此,为了选择容量最小的一个,我们惩罚较大的I(X,Z),将其添加到原始的IRM公式中。为此,我们将目标定为:
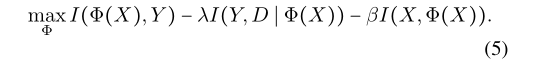
其中第一项和第三项是information bottleneck,第二项是IRM 准则。(5)公式就是IIB准则。
LOSS FUNCTION 设计:
(5)中的目标仍然不是一个易于处理的损失函数,因为高维向量的互信息难以估计。与VIB (Alemi et al. 2017)类似,我们利用变分逼近来解决这个问题。
设r(z)近似于真实的边际p(z), q(y∣z)近似于p(y∣z),同时,让p(z|x)作为随机编码器。现在我们的
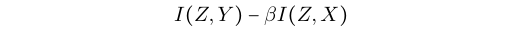
可以被写作:
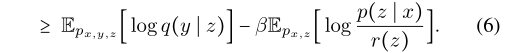
优化(6)仍然是一项艰巨的任务。然后用再参数化操作对其进行变换:
我们使用encoder :
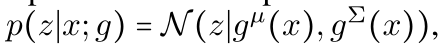
g输出一个K维度的平均值μ和一个KxK维度的协方差矩阵∑。然后通过改变变量公式,我们会有

我们然后去处理I(Y,D|Z)。根据变分近似的规则(FarniaandTse2016),我们有:
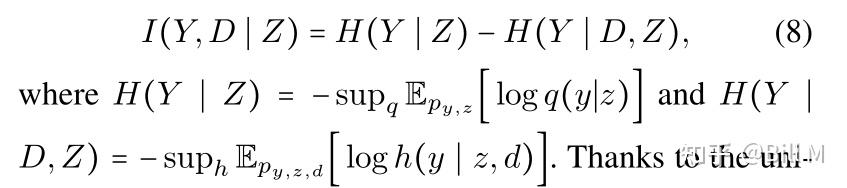
感谢神经网络的普遍逼近能力,(8)可记为减去两个分类损失(Farnia和Tse 2016):
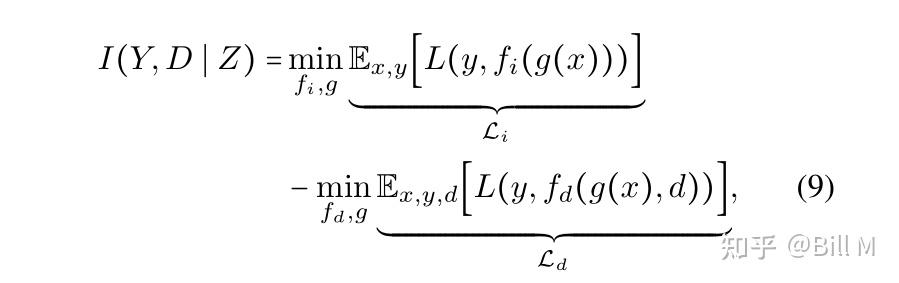
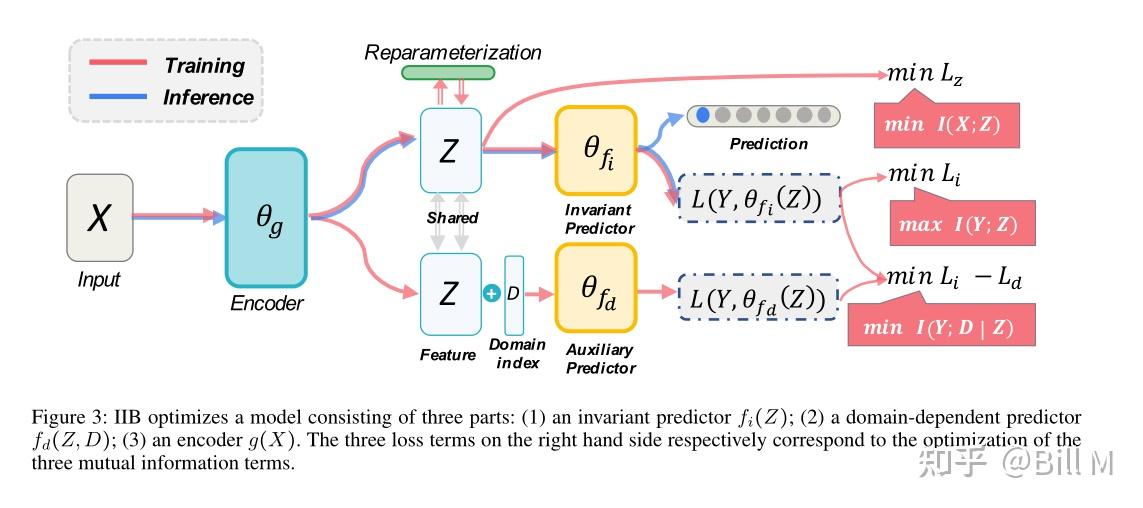
其中fi以特征z为输入,f (d),d = 1,⋯,d以特征z和定义域指标d为输入。总的来说,我们可以通过优化IIB目标函数的可处理下界来最大化我们的IIB目标函数:
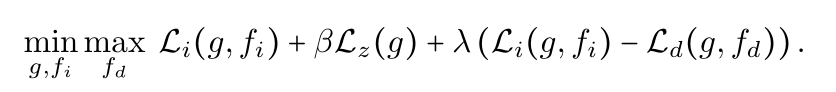
在上述目标函数的指导下,如图3所示,IIB优化了一个由三部分组成的模型:(1)不变预测器fi(Z) (Z);(2)域依赖的预测期fd(Z,D) (3)encoder g(X)
右边的三个损失项分别对应三个互信息项的优化。
模拟合成实验
实验设置
为了验证IIB对伪不变特征和几何歪斜影响的缓解效果,我们采用了两种类型的合成实验。两种实验均存在伪不变特征和几何歪斜。
CS-CMNIST (Ahuja et al. 2021)是一种十向分类任务。这些图像都来自MNIST。有三个环境,两个训练环境包含每个20000张图像,一个测试环境包含20000张图像。有十种颜色与十位数相对应。概率pe表示图像是带有相关颜色的。
在两种训练环境下,将pe分别设为1和0.9,即对某一类图像分别以pe概率的关联颜色进行着色,以1−p e概率的随机颜色进行着色。
在测试环境中,pe设置为0,这意味着所有的图像都是随机着色的。总的来说,训练区域的图像颜色可以完全预测出带有伪特征的拉贝尔图像,即使用相关的颜色,但测试区域的信息会消失。
在CS-CMNIST中,如果测试时准确率下降更多,说明训练过程中更依赖于伪特征。我们将给出AC-CMNIST的IIB结果(在DomainBed中它被称为CMNIST)。
略
结论:
由于现有的IRM方法在领域泛化中的局限性,本文提出了一种新的信息论方法来克服这些问题。我们将我们的新目标称为不变信息瓶颈(IIB)。
我们在设计IIB时的关键见解在于, 当训练域的数量不足以识别所有潜在的虚假特征时,我们应该在所有满足原始IRM目标的潜在特征中,寻找那些具有最小容量的特征 。
为了实现IIB,我们提出了一种变分方法来优化目标函数,它超越了之前的梯度惩罚公式,这只适用于线性分类器。
通过大量的实验,在合成数据集和真实数据集上都证明了其优越的性能。将信息bot- tleneck原理应用于非线性不变量因果预测的理论基础以及IIB在回归任务中的有效性是未来研究的重点。
========================================================
Empirical risk minimizationd
针对定义错的情况,我们定义expected risk,P(x,y)一个事件发生的概率,l-loss function,乘以这个事件发生的值,f是feature,x,y就是在P中采样的sample。

P是一个未知的分布。δ表示在整个数据集中数据正好是xi,yi的概率,有一个复杂的假设,这里只介绍。



========================================================
