扩散模型之DDPM

小小将

华中科技大学工学硕士

“ What I cannot create, I do not understand .” -- Richard Feynman

近段时间最火的方向无疑是 基于文本用AI生成图像 ，继OpenAI在2021提出的文本转图像模型 DALLE 之后，越来越多的大公司卷入这个方向，如谷歌在今年相继推出了 Imagen 和 Parti 。一些主流的文本转图像模型如 DALL·E 2 ， stable-diffusion 和 Imagen 采用了 扩散模型 （ Diffusion Model ）作为图像生成模型，这也引发了对扩散模型的研究热潮。相比GAN来说，扩散模型训练更稳定，而且能够生成更多样的样本，OpenAI的论文 Diffusion Models Beat GANs on Image Synthesis 也证明了扩散模型能够超越GAN。简单来说，扩散模型包含两个过程： 前向扩散过程 和 反向生成过程 ，前向扩散过程是对一张图像逐渐添加高斯噪音直至变成 随机噪音 ，而反向生成过程是 去噪音过程 ，我们将从一个随机噪音开始逐渐去噪音直至生成一张图像，这也是我们要求解或者训练的部分。扩散模型与其它主流生成模型的对比如下所示：

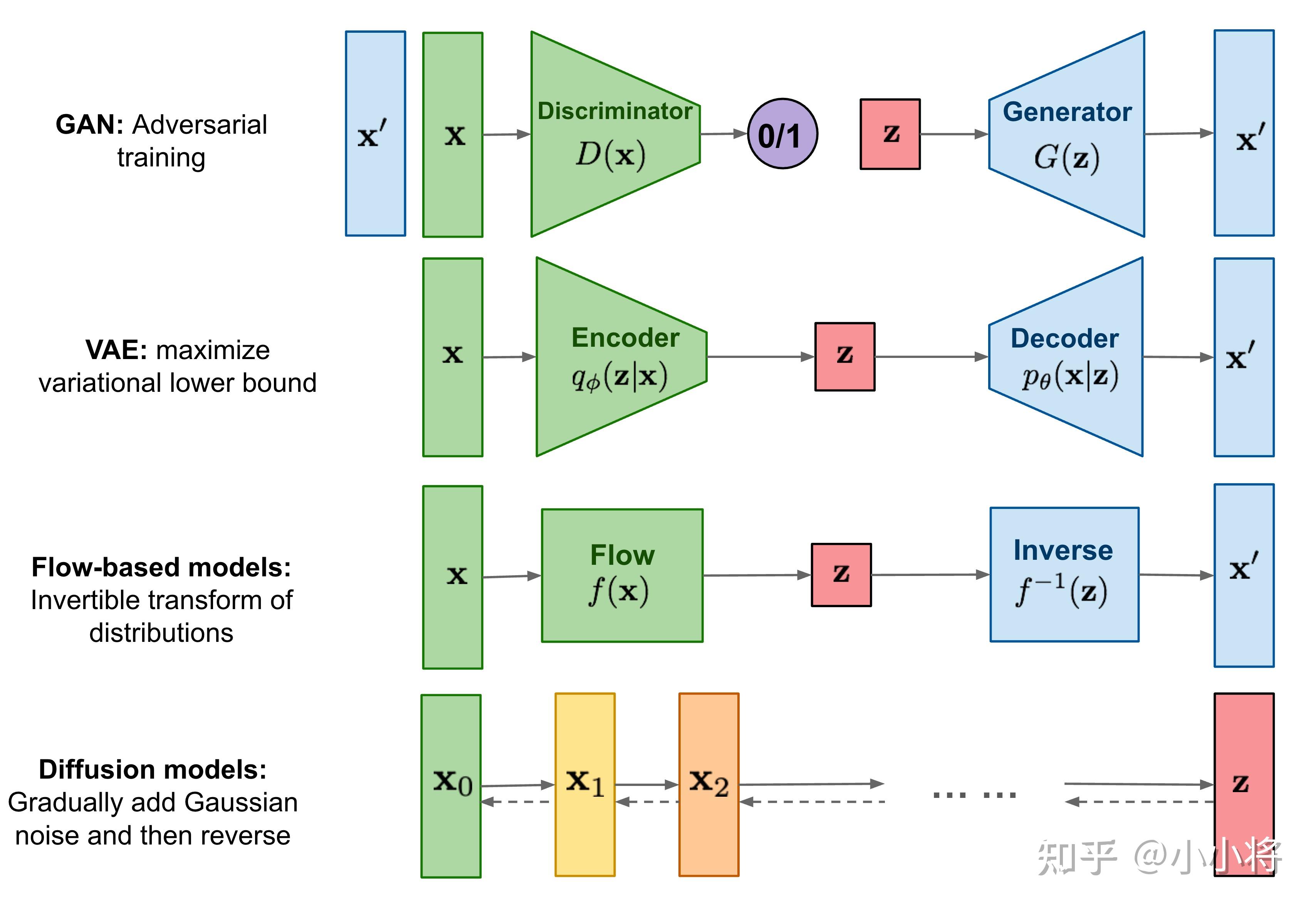
目前所采用的扩散模型大都是来自于2020年的工作 DDPM: Denoising Diffusion Probabilistic Models ， DDPM对之前的扩散模型（具体见 Deep Unsupervised Learning using Nonequilibrium Thermodynamics ）进行了简化，并通过 变分推断 （variational inference）来进行建模，这主要是因为扩散模型也是一个 隐变量模型 （latent variable model），相比VAE这样的隐变量模型，扩散模型的隐变量是和原始数据是同维度的，而且推理过程（即扩散过程）往往是固定的。这篇文章将基于DDPM详细介绍扩散模型的原理，并给出具体的代码实现和分析。

扩散模型原理

扩散模型包括两个过程： 前向过程（forward process） 和 反向过程（reverse process） ，其中前向过程又称为 扩散过程（diffusion process） ，如下图所示。无论是前向过程还是反向过程都是一个 参数化的马尔可夫链（Markov chain） ，其中反向过程可以用来生成数据，这里我们将通过变分推断来进行建模和求解。

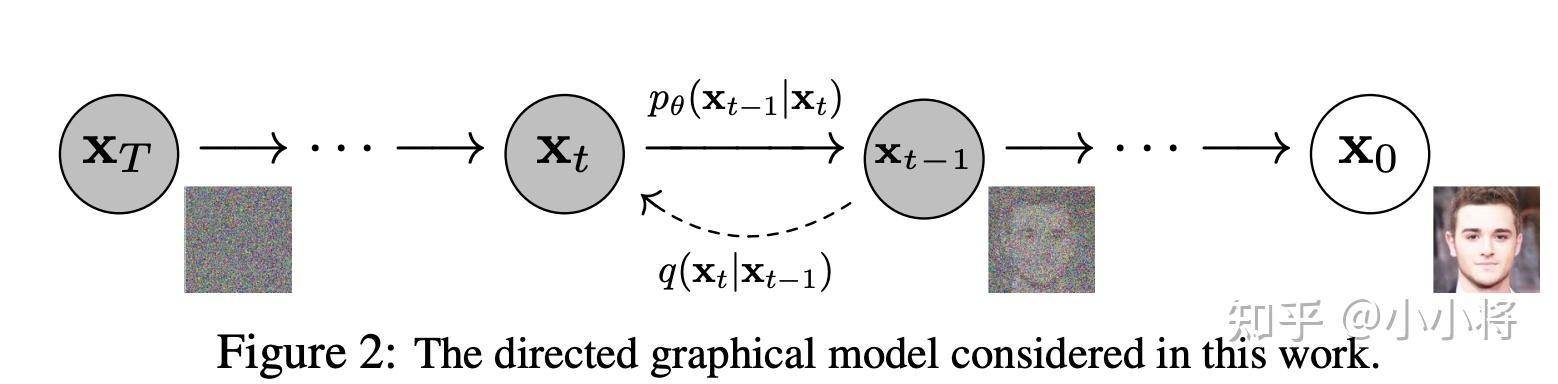
扩散过程

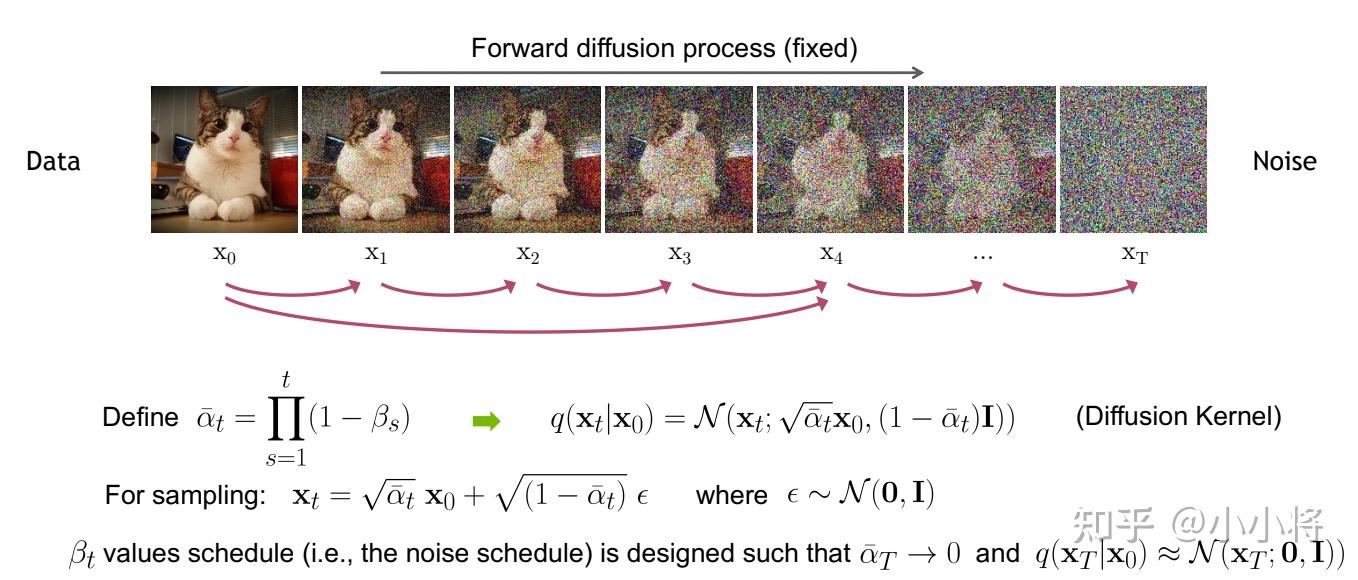
扩散过程是指的对数据逐渐增加高斯噪音直至数据变成随机噪音的过程。对于原始数据 \mathbf{x}_0 \sim q(\mathbf{x}_0) ，总共包含 T 步的扩散过程的每一步都是对上一步得到的数据 \mathbf{x}_{t-1} 按如下方式增加高斯噪音：

q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) \\

这里 \{\beta_t\}^T_{t=1} 为每一步所采用的方差，它介于0～1之间。对于扩散模型，我们往往称不同step的方差设定为 variance schedule 或者 noise schedule ，通常情况下，越后面的step会采用更大的方差，即满足 \beta_1 < \beta_2 < \dots < \beta_T 。在一个设计好的 variance schedule 下，的如果扩散步数 T 足够大，那么最终得到的 \mathbf{x}_{T} 就完全丢失了原始数据而变成了一个随机噪音。扩散过程的每一步都生成一个带噪音的数据 \mathbf{x}_{t} ，整个扩散过程也就是一个 马尔卡夫链 ：

q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) \\

另外要指出的是，扩散过程往往是固定的，即采用一个预先定义好的 variance schedule ，比如DDPM就采用一个线性的 variance schedule 。

扩散过程的一个重要特性是我们可以 直接基于原始数据 \mathbf{x}_{0} 来对任意 t 步的 \mathbf{x}_{t} 进行采样： \mathbf{x}_{t}\sim q(\mathbf{x}_t \vert \mathbf{x}_0) 。这里定义 \alpha_t = 1 - \beta_t 和 \bar{\alpha}_t = \prod_{i=1}^t \alpha_i ，通过 重参数技巧 （和VAE类似），那么有：

\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\mathbf{\epsilon}_{t-1} & \text{ ;where } \mathbf{\epsilon}_{t-1}, \mathbf{\epsilon}_{t-2}, \dots \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}\mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}}\mathbf{\epsilon}_{t-2}) + \sqrt{1 - \alpha_t}\mathbf{\epsilon}_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{\sqrt {\alpha_t-\alpha_t \alpha_{t-1}}^2+\sqrt{1-\alpha_t }^2} \bar{\mathbf{\epsilon}}_{t-2} & \text{ ;where } \bar{\mathbf{\epsilon}}_{t-2} \text{ merges two Gaussians (*).} \\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\mathbf{\epsilon}}_{t-2} \\ &= \dots \\ &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon} \end{aligned}\\

上述推到过程利用了两个方差不同的高斯分布 \mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I}) 和 \mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I}) 相加等于一个新的高斯分布 \mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I}) 。反重参数化后，我们得到：

q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \\

扩散过程的这个特性很重要。首先，我们可以看到 \mathbf{x}_{t} 其实可以看成是原始数据 \mathbf{x}_{0} 和随机噪音 \mathbf{\epsilon} 的线性组合，其中 \sqrt{\bar \alpha_t} 和 \sqrt{1 - \bar{\alpha}_t} 为组合系数，它们的平方和等于1，我们也可以称两者分别为 signal_rate 和 noise_rate （见 https:// keras.io/examples/gener ative/ddim/#diffusion-schedule 和 Variational Diffusion Models ）。更近一步地，我们可以基于 \bar \alpha_t 而不是 \beta_t 来定义 noise schedule （见 Improved Denoising Diffusion Probabilistic Models 所设计的cosine schedule），因为这样处理更直接，比如我们直接将 \bar \alpha_T 设定为一个接近0的值，那么就可以保证最终得到的 \mathbf{x}_{T} 近似为一个随机噪音。其次，后面的建模和分析过程将使用这个特性。

反向过程

扩散过程是将数据噪音化，那么反向过程就是 一个去噪的过程 ，如果我们知道反向过程的每一步的真实分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) ，那么从一个随机噪音 \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) 开始，逐渐去噪就能生成一个真实的样本，所以反向过程也就是 生成数据的过程 。

估计分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 需要用到整个训练样本，我们可以用神经网络来估计这些分布。这里，我们将反向过程也定义为一个马尔卡夫链，只不过它是由一系列 用神经网络参数化的高斯分布 来组成：

p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\\

这里 p(\mathbf{x}_T)= \mathcal{N}(\mathbf{x}_T;\mathbf{0}, \mathbf{I}) ，而 p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 为参数化的高斯分布，它们的均值和方差由训练的网络 \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) 和 \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) 给出。实际上， 扩散模型就是要得到这些训练好的网络，因为它们构成了最终的生成模型 。

虽然分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 是不可直接处理的，但是加上条件 \mathbf{x}_0 的后验分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 却是可处理的，这里有：

q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), \color{red}{\tilde{\beta}_t} \mathbf{I}) \\

下面我们来具体推导这个分布，首先根据贝叶斯公式，我们有：

q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) }\\

由于扩散过程的马尔卡夫链特性，我们知道分布 q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0)=q(\mathbf{x}_t \vert \mathbf{x}_{t-1})=\mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) （这里条件 \mathbf{x}_0 是多余的），而由前面得到的扩散过程特性可知：

q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0, (1 - \bar{\alpha}_{t-1})\mathbf{I})，q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \\

所以，我们有：

\begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned}\\

这里的 C(\mathbf{x}_t, \mathbf{x}_0) 是一个和 \mathbf{x}_{t-1} 无关的部分，所以省略。根据高斯分布的概率密度函数定义和上述结果（配平方），我们可以得到后验分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_{t}, \mathbf{x}_0) 的均值和方差：

\begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}) = \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) \color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned}\\

可以看到方差是一个定量（扩散过程参数固定），而均值是一个依赖 \mathbf{x}_0 和 \mathbf{x}_t 的函数。这个分布将会被用于推导扩散模型的优化目标。

优化目标

上面介绍了扩散模型的扩散过程和反向过程，现在我们来从另外一个角度来看扩散模型：如果我们把中间产生的变量看成隐变量的话，那么扩散模型其实是包含 T 个隐变量的 隐变量模型（latent variable model） ，它可以看成是一个特殊的 Hierarchical VAEs （见 Understanding Diffusion Models: A Unified Perspective ）：

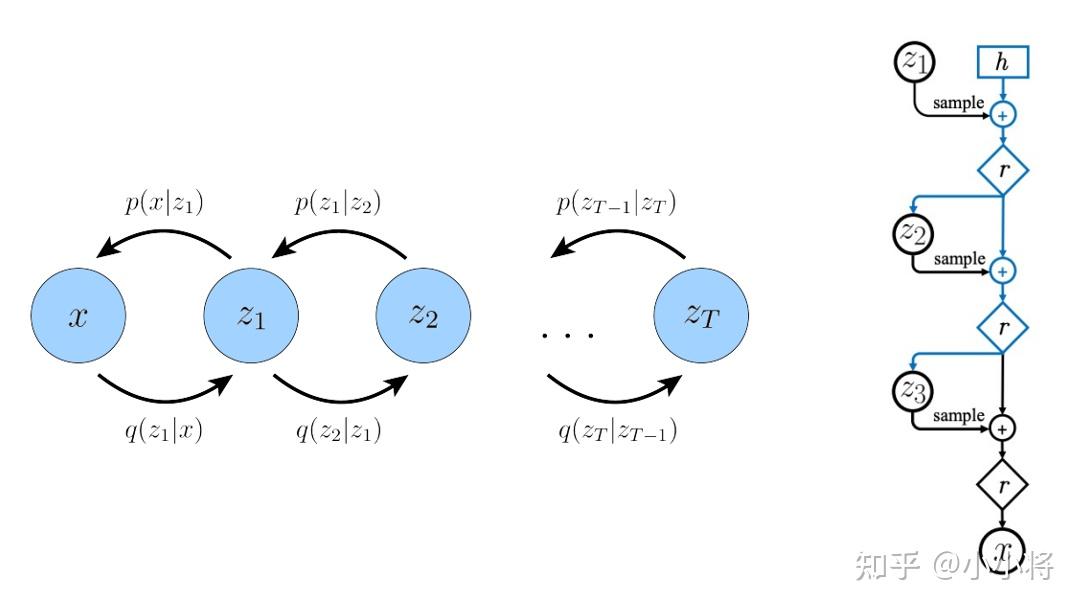
相比VAE来说，扩散模型的隐变量是和原始数据同维度的，而且encoder（即扩散过程）是固定的。既然扩散模型是隐变量模型，那么我们可以就可以基于 变分推断 来得到 variational lower bound （ VLB ，又称 ELBO ）作为最大化优化目标，这里有：

\begin{aligned} \log p_\theta(\mathbf{x}_0) &=\log\int p_\theta(\mathbf{x}_{0:T}) d\mathbf{x}_{1:T}\\ &=\log\int \frac{p_\theta(\mathbf{x}_{0:T}) q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} d\mathbf{x}_{1:T}\\ &\geq \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}[\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}]\\ \end{aligned}\\

这里最后一步是利用了 Jensen's inequality （不采用这个不等式的推导见博客 What are Diffusion Models? ），对于网络训练来说，其训练目标为 VLB取负 ：

L=-L_{\text{VLB}}=\mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}[-\log \frac{p_\theta(\mathbf{x}_{0:T})}{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}]=\mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}[\log \frac{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{0:T})}] \\

我们近一步对训练目标进行分解可得：

\begin{aligned} L &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1}, \mathbf{x}_{0})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] & \text{ ;use } q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0)=q(\mathbf{x}_t \vert \mathbf{x}_{t-1})\\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] & \text{ ;use Bayes' Rule }\\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_{q(\mathbf{x}_{1:T}\vert \mathbf{x}_{0})} \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{T}\vert \mathbf{x}_{0})}\Big[\log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)}\Big]+\sum_{t=2}^T \mathbb{E}_{q(\mathbf{x}_{t}, \mathbf{x}_{t-1}\vert \mathbf{x}_{0})}\Big[\log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\Big] - \mathbb{E}_{q(\mathbf{x}_{1}\vert \mathbf{x}_{0})}\Big[\log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)\Big] \\ &= \mathbb{E}_{q(\mathbf{x}_{T}\vert \mathbf{x}_{0})}\Big[\log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)}\Big]+\sum_{t=2}^T \mathbb{E}_{q(\mathbf{x}_{t}\vert \mathbf{x}_{0})}\Big[q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\Big] - \mathbb{E}_{q(\mathbf{x}_{1}\vert \mathbf{x}_{0})}\Big[\log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)\Big] \\ &= \underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{\mathbb{E}_{q(\mathbf{x}_{t}\vert \mathbf{x}_{0})}\Big[D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))\Big]}_{L_{t-1}} -\underbrace{\mathbb{E}_{q(\mathbf{x}_{1}\vert \mathbf{x}_{0})}\log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} \end{aligned}

可以看到最终的优化目标共包含 T+1 项，其中 L_0 可以看成是原始数据重建，优化的是负对数似然， L_0 可以用估计的 \mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1)) 来构建一个离散化的decoder来计算（见DDPM论文3.3部分）：

p_{\theta}(\mathbf{x}_0\vert\mathbf{x}_1)=\prod^D_{i=1}\int ^{\delta_+(x_0^i)}_{\delta_-(x_0^i)}\mathcal{N}(x_0; \mu^i_\theta(x_1, 1), \Sigma^i_\theta(x_1, 1))dx\\ \delta_+(x)= \begin{cases} \infty& \text{ if } x=1 \\ x+\frac{1}{255}& \text{ if } x <1 \end{cases} \\ \delta_+(x)= \begin{cases} -\infty& \text{ if } x=-1 \\ x-\frac{1}{255}& \text{ if } x >-1 \end{cases}

在DDPM中，会将原始图像的像素值从[0, 255]范围归一化到[-1, 1]，像素值属于离散化值，这样不同的像素值之间的间隔其实就是2/255，我们可以计算高斯分布落在以ground truth为中心且范围大小为2/255时的概率积分即CDF，具体实现见 https:// github.com/hojonathanho /diffusion/blob/master/diffusion_tf/utils.py#L116-L133 （不过后面我们的简化版优化目标并不会计算这个对数似然）。

而 L_T 计算的是最后得到的噪音的分布和先验分布的KL散度，这个KL散度没有训练参数，近似为0，因为先验 p(\mathbf {x}_T)=\mathcal{N}(\mathbf{0}, \mathbf{I}) 而扩散过程最后得到的随机噪音 q(\mathbf{x}_{T}\vert \mathbf{x}_{0}) 也近似为 \mathcal{N}(\mathbf{0}, \mathbf{I}) ；而 L_{t-1} 则是计算的是估计分布 p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) 和真实后验分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 的KL散度，这里希望我们估计的去噪过程和依赖真实数据的去噪过程近似一致：

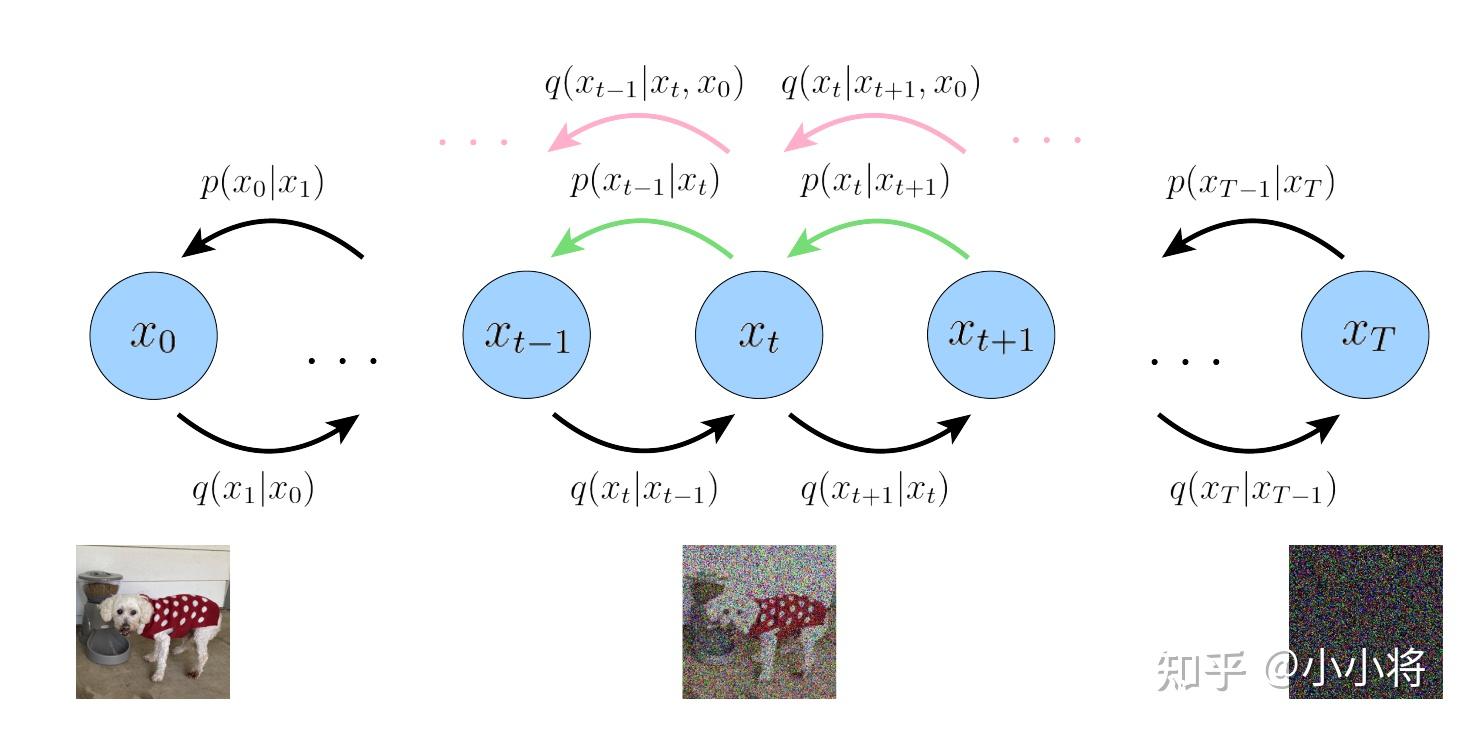
之所以前面我们将 p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) 定义为一个用网络参数化的高斯分布 \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) ，是因为要匹配的后验分布 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 也是一个高斯分布。对于训练目标 L_0 和 L_{t-1} 来说，都是希望得到训练好的网络 \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) 和 \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) （对于 L_0 ， t=1 ）。DDPM对 p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) 做了近一步简化， 采用固定的方差 ： \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)= \sigma_t^2\mathbf{I} ，这里的 \sigma_t^2 可以设定为 \beta _t 或者 \tilde{\beta}_t （这其实是两个极端，分别是上限和下限，也可以采用可训练的方差，见论文 Improved Denoising Diffusion Probabilistic Models 和 Analytic-DPM: an Analytic Estimate of the Optimal Reverse Variance in Diffusion Probabilistic Models ）。这里假定 \sigma_t^2=\tilde{\beta}_t ，那么：

q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)=\mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}} (\mathbf{x}_t, \mathbf{x}_0), {\sigma_t^2} \mathbf{I}) p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), {\sigma_t^2} \mathbf{I})

对于两个高斯分布的KL散度，其计算公式为（具体推导见生成模型之VAE ）：

\text{KL}(p_1||p_2) = \frac{1}{2}(\text{tr}(\boldsymbol{\Sigma}_2^{-1}\boldsymbol{\Sigma}_1)+(\boldsymbol{\mu_2}-\boldsymbol{\mu_1})^{\top}\boldsymbol{\Sigma}_2^{-1}(\boldsymbol{\mu_2}-\boldsymbol{\mu_1})-n+\log\frac{\det(\boldsymbol{\Sigma_2})}{\det(\boldsymbol{\Sigma_1})}) \\

那么就有：

\begin{aligned} D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)\parallel p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)) &=D_\text{KL}(\mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}} (\mathbf{x}_t, \mathbf{x}_0), {\sigma_t^2} \mathbf{I}) \parallel \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), {\sigma_t^2} \mathbf{I})) \\ &=\frac{1}{2}(n+\frac{1}{{\sigma_t^2}}\|\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 -n+\log1) \\ &=\frac{1}{2{\sigma_t^2}}\|\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \end{aligned}\\

那么优化目标 L_{t-1} 即为：

L_{t-1}=\mathbb{E}_{q(\mathbf{x}_{t}\vert \mathbf{x}_{0})}\Big[ \frac{1}{2{\sigma_t^2}}\|\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2\Big] \\

从上述公式来看，我们是希望网络学习到的均值 \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) 和后验分布的均值 {\tilde{\boldsymbol{\mu}}} (\mathbf{x}_t, \mathbf{x}_0) 一致。不过DDPM发现预测均值并不是最好的选择。根据前面得到的扩散过程的特性，我们有：

\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon})=\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon} \quad \text{ where } \mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\

将这个公式带入上述优化目标（注意这里的损失我们加上了对 \mathbf{x}_0 的数学期望），可以得到：

\begin{aligned} L_{t-1}&=\mathbb{E}_{\mathbf{x}_{0}}\Big(\mathbb{E}_{q(\mathbf{x}_{t}\vert \mathbf{x}_{0})}\Big[ \frac{1}{2{\sigma_t^2}}\|\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0) - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2\Big]\Big) \\ &=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{1}{2{\sigma_t^2}}\|\tilde{\boldsymbol{\mu}}_t\Big(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), \frac{1}{\sqrt{\bar \alpha_t}} \big(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}) - \sqrt{1 - \bar{\alpha}_t} \mathbf{\epsilon} \big)\Big ) - {\boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t)} \|^2\Big] \\ &=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{1}{2{\sigma_t^2}}\|\Big (\frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}) + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar \alpha_t}} \big(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}) - \sqrt{1 - \bar{\alpha}_t} \mathbf{\epsilon} \big) \Big) - {\boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t)} \|^2\Big] \\ &=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{1}{2{\sigma_t^2}}\|\frac{1}{\sqrt{\alpha_t}}\Big( \mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}\mathbf{\epsilon}\Big) - {\boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t)} \|^2\Big] \end{aligned}\\

近一步地，我们对 \boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t) 也进行重参数化，变成：

\boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t)=\frac{1}{\sqrt{\alpha_t}}\Big( \mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}\mathbf{\epsilon}_\theta\big(\mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}), t\big)\Big) \\

这里的 \mathbf{\epsilon}_\theta 是一个基于神经网络的拟合函数，这意味着我们 由原来的预测均值而换成预测噪音 \mathbf{\epsilon} 。我们将上述等式带入优化目标，可以得到：

\begin{aligned} L_{t-1}&=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{1}{2{\sigma_t^2}}\|\frac{1}{\sqrt{\alpha_t}}\Big( \mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}\mathbf{\epsilon}\Big) - {\boldsymbol{\mu}_\theta(\mathbf{x_t}(\mathbf{x_0},\mathbf{\epsilon}), t)} \|^2\Big] \\ &= \mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{\beta_t^2}{2{\sigma_t^2}\alpha_t(1-\bar{\alpha}_t)}\| \mathbf{\epsilon}- \mathbf{\epsilon}_\theta\big(\mathbf{x}_t(\mathbf{x_0},\mathbf{\epsilon}), t\big)\|^2\Big]\\ &=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \frac{\beta_t^2}{2{\sigma_t^2}\alpha_t(1-\bar{\alpha}_t)}\| \mathbf{\epsilon}- \mathbf{\epsilon}_\theta\big(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon}, t\big)\|^2\Big] \end{aligned}\\

DDPM近一步对上述目标进行了简化，即去掉了权重系数，变成了： L_{t-1}^{\text{simple}}=\mathbb{E}_{\mathbf{x}_{0},\mathbf{\epsilon}\sim \mathcal{N}(\mathbf{0}, \mathbf{I})}\Big[ \| \mathbf{\epsilon}- \mathbf{\epsilon}_\theta\big(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\mathbf{\epsilon}, t\big)\|^2\Big]

这里的 t 在[1, T]范围内取值（如前所述，其中取1时对应 L_0 ）。由于去掉了不同 t 的权重系数，所以这个简化的目标其实是VLB优化目标进行了reweight。从DDPM的对比实验结果来看，预测噪音比预测均值效果要好，采用简化版本的优化目标比VLB目标效果要好：

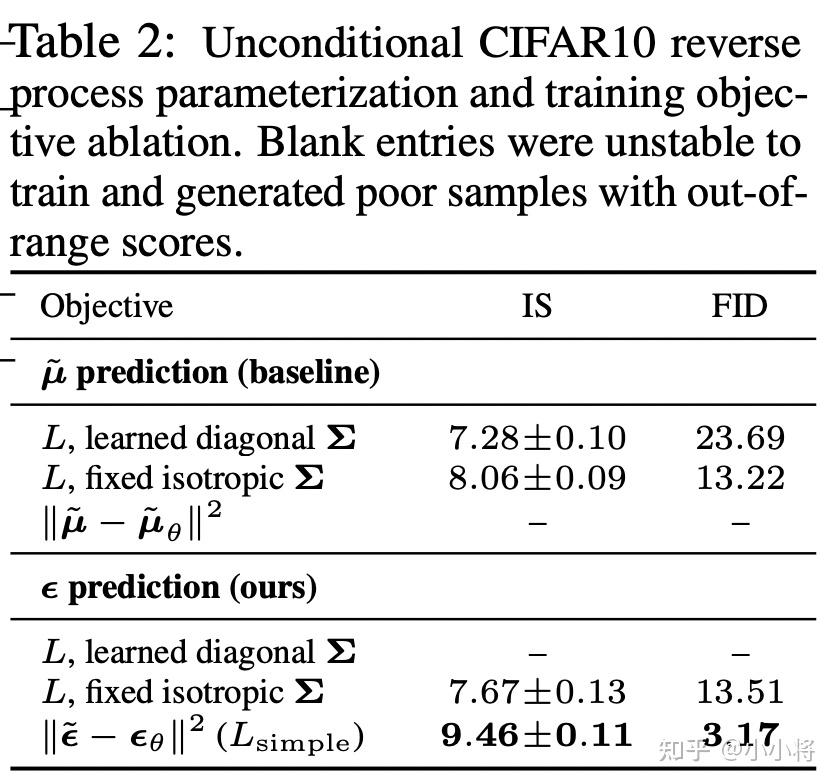
虽然扩散模型背后的推导比较复杂，但是我们最终得到的优化目标非常简单，就是让网络预测的噪音和真实的噪音一致。DDPM的训练过程也非常简单，如下图所示：随机选择一个训练样本->从1-T随机抽样一个t->随机产生噪音-计算当前所产生的带噪音数据（红色框所示）->输入网络预测噪音->计算产生的噪音和预测的噪音的L2损失->计算梯度并更新网络。

一旦训练完成，其采样过程也非常简单，如上所示：我们从一个随机噪音开始，并用训练好的网络预测噪音，然后计算条件分布的均值（红色框部分），然后用均值加标准差乘以一个随机噪音，直至t=0完成新样本的生成（最后一步不加噪音）。不过实际的代码实现和上述过程略有区别（见 https:// github.com/hojonathanho /diffusion/issues/5 ：先基于预测的噪音生成 \mathbf{x}_0 ，并进行了 clip处理 （范围[-1, 1]，原始数据归一化到这个范围），然后再计算均值。我个人的理解这应该算是一种约束，既然模型预测的是噪音，那么我们也希望用预测噪音重构处理的原始数据也应该满足范围要求。

模型设计

前面我们介绍了扩散模型的原理以及优化目标，那么扩散模型的核心就在于训练噪音预测模型，由于噪音和原始数据是同维度的，所以我们可以选择采用 AutoEncoder架构 来作为噪音预测模型。DDPM所采用的模型是一个基于residual block和attention block的 U-Net模型 。如下所示：

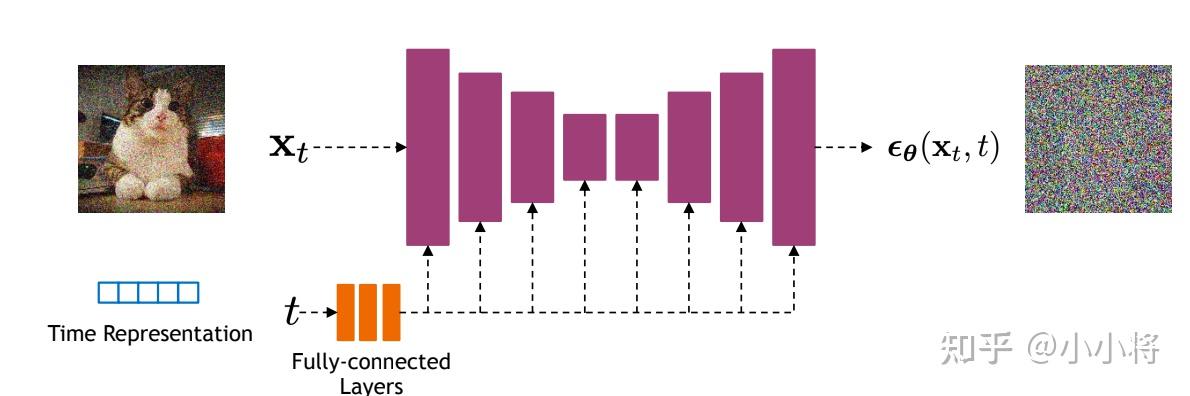
U-Net属于encoder-decoder架构，其中encoder分成不同的stages，每个stage都包含下采样模块来降低特征的空间大小（H和W），然后decoder和encoder相反，是将encoder压缩的特征逐渐恢复。U-Net在decoder模块中还引入了 skip connection ，即concat了encoder中间得到的同维度特征，这有利于网络优化。DDPM所采用的U-Net每个stage包含 2个residual block ，而且部分stage还加入了 self-attention模块 增加网络的全局建模能力。另外，扩散模型其实需要的是 T 个噪音预测模型，实际处理时，我们可以增加一个 time embedding （类似transformer中的position embedding）来将timestep编码到网络中，从而只需要训练一个共享的U-Net模型。具体地，DDPM在各个residual block都引入了 time embedding ，如上图所示。

代码实现

最后，我们基于PyTorch框架给出DDPM的具体实现，这里主要参考了三套代码实现：

GitHub - hojonathanho/diffusion: Denoising Diffusion Probabilistic Models （官方TensorFlow实现）
GitHub - openai/improved-diffusion: Release for Improved Denoising Diffusion Probabilistic Models （OpenAI基于PyTorch实现的DDPM+）
GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch

首先，是time embeding，这里是采用 Attention Is All You Need 中所设计的 sinusoidal position embedding ，只不过是用来编码timestep：

# use sinusoidal position embedding to encode time step (https://arxiv.org/abs/1706.03762)   
def timestep_embedding(timesteps, dim, max_period=10000):
    Create sinusoidal timestep embeddings.
    :param timesteps: a 1-D Tensor of N indices, one per batch element.
                      These may be fractional.
    :param dim: the dimension of the output.
    :param max_period: controls the minimum frequency of the embeddings.
    :return: an [N x dim] Tensor of positional embeddings.
    half = dim // 2
    freqs = torch.exp(
        -math.log(max_period) * torch.arange(start=0, end=half, dtype=torch.float32) / half
    ).to(device=timesteps.device)
    args = timesteps[:, None].float() * freqs[None]
    embedding = torch.cat([torch.cos(args), torch.sin(args)], dim=-1)
    if dim % 2:
        embedding = torch.cat([embedding, torch.zeros_like(embedding[:, :1])], dim=-1)
    return embedding

由于只有residual block才引入time embedding，所以可以定义一些辅助模块来自动处理，如下所示：

# define TimestepEmbedSequential to support `time_emb` as extra input
class TimestepBlock(nn.Module):
    Any module where forward() takes timestep embeddings as a second argument.
    @abstractmethod
    def forward(self, x, emb):
        Apply the module to `x` given `emb` timestep embeddings.
class TimestepEmbedSequential(nn.Sequential, TimestepBlock):
    A sequential module that passes timestep embeddings to the children that
    support it as an extra input.
    def forward(self, x, emb):
        for layer in self:
            if isinstance(layer, TimestepBlock):
                x = layer(x, emb)
            else:
                x = layer(x)
        return x

这里所采用的U-Net采用 GroupNorm进行归一化 ，所以这里也简单定义了一个norm layer以方便使用：

# use GN for norm layer
def norm_layer(channels):
    return nn.GroupNorm(32, channels)

U-Net的核心模块是residual block，它包含两个卷积层以及shortcut，同时也要引入time embedding，这里额外定义了一个linear层来将time embedding变换为和特征维度一致，第一conv之后通过加上time embedding来编码time：

# Residual block
class ResidualBlock(TimestepBlock):
    def __init__(self, in_channels, out_channels, time_channels, dropout):
        super().__init__()
        self.conv1 = nn.Sequential(
            norm_layer(in_channels),
            nn.SiLU(),
            nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=1)
        # pojection for time step embedding
        self.time_emb = nn.Sequential(
            nn.SiLU(),
            nn.Linear(time_channels, out_channels)
        self.conv2 = nn.Sequential(
            norm_layer(out_channels),
            nn.SiLU(),
            nn.Dropout(p=dropout),
            nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
        if in_channels != out_channels:
            self.shortcut = nn.Conv2d(in_channels, out_channels, kernel_size=1)
        else:
            self.shortcut = nn.Identity()
    def forward(self, x, t):
        `x` has shape `[batch_size, in_dim, height, width]`
        `t` has shape `[batch_size, time_dim]`
        h = self.conv1(x)
        # Add time step embeddings
        h += self.time_emb(t)[:, :, None, None]
        h = self.conv2(h)
        return h + self.shortcut(x)

这里还在部分residual block引入了attention，这里的attention和transformer的self-attention是一致的：

# Attention block with shortcut
class AttentionBlock(nn.Module):
    def __init__(self, channels, num_heads=1):
        super().__init__()
        self.num_heads = num_heads
        assert channels % num_heads == 0
        self.norm = norm_layer(channels)
        self.qkv = nn.Conv2d(channels, channels * 3, kernel_size=1, bias=False)
        self.proj = nn.Conv2d(channels, channels, kernel_size=1)
    def forward(self, x):
        B, C, H, W = x.shape
        qkv = self.qkv(self.norm(x))
        q, k, v = qkv.reshape(B*self.num_heads, -1, H*W).chunk(3, dim=1)
        scale = 1. / math.sqrt(math.sqrt(C // self.num_heads))
        attn = torch.einsum("bct,bcs->bts", q * scale, k * scale)
        attn = attn.softmax(dim=-1)
        h = torch.einsum("bts,bcs->bct", attn, v)
        h = h.reshape(B, -1, H, W)
        h = self.proj(h)
        return h + x

对于上采样模块和下采样模块，其分别可以采用插值和stride=2的conv或者pooling来实现：

# upsample
class Upsample(nn.Module):
    def __init__(self, channels, use_conv):
        super().__init__()
        self.use_conv = use_conv
        if use_conv:
            self.conv = nn.Conv2d(channels, channels, kernel_size=3, padding=1)
    def forward(self, x):
        x = F.interpolate(x, scale_factor=2, mode="nearest")
        if self.use_conv:
            x = self.conv(x)
        return x
# downsample
class Downsample(nn.Module):
    def __init__(self, channels, use_conv):
        super().__init__()
        self.use_conv = use_conv
        if use_conv:
            self.op = nn.Conv2d(channels, channels, kernel_size=3, stride=2, padding=1)
        else:
            self.op = nn.AvgPool2d(stride=2)
    def forward(self, x):
        return self.op(x)

上面我们实现了U-Net的所有组件，就可以进行组合来实现U-Net了：

# The full UNet model with attention and timestep embedding
class UNetModel(nn.Module):
    def __init__(
        self,
        in_channels=3,
        model_channels=128,
        out_channels=3,
        num_res_blocks=2,
        attention_resolutions=(8, 16),
        dropout=0,
        channel_mult=(1, 2, 2, 2),
        conv_resample=True,
        num_heads=4
        super().__init__()
        self.in_channels = in_channels
        self.model_channels = model_channels
        self.out_channels = out_channels
        self.num_res_blocks = num_res_blocks
        self.attention_resolutions = attention_resolutions
        self.dropout = dropout
        self.channel_mult = channel_mult
        self.conv_resample = conv_resample
        self.num_heads = num_heads
        # time embedding
        time_embed_dim = model_channels * 4
        self.time_embed = nn.Sequential(
            nn.Linear(model_channels, time_embed_dim),
            nn.SiLU(),
            nn.Linear(time_embed_dim, time_embed_dim),
        # down blocks
        self.down_blocks = nn.ModuleList([
            TimestepEmbedSequential(nn.Conv2d(in_channels, model_channels, kernel_size=3, padding=1))
        down_block_chans = [model_channels]
        ch = model_channels
        ds = 1
        for level, mult in enumerate(channel_mult):
            for _ in range(num_res_blocks):
                layers = [
                    ResidualBlock(ch, mult * model_channels, time_embed_dim, dropout)
                ch = mult * model_channels
                if ds in attention_resolutions:
                    layers.append(AttentionBlock(ch, num_heads=num_heads))
                self.down_blocks.append(TimestepEmbedSequential(*layers))
                down_block_chans.append(ch)
            if level != len(channel_mult) - 1: # don't use downsample for the last stage
                self.down_blocks.append(TimestepEmbedSequential(Downsample(ch, conv_resample)))
                down_block_chans.append(ch)
                ds *= 2
        # middle block
        self.middle_block = TimestepEmbedSequential(
            ResidualBlock(ch, ch, time_embed_dim, dropout),
            AttentionBlock(ch, num_heads=num_heads),
            ResidualBlock(ch, ch, time_embed_dim, dropout)
        # up blocks
        self.up_blocks = nn.ModuleList([])
        for level, mult in list(enumerate(channel_mult))[::-1]:
            for i in range(num_res_blocks + 1):
                layers = [
                    ResidualBlock(
                        ch + down_block_chans.pop(),
                        model_channels * mult,
                        time_embed_dim,
                        dropout
                ch = model_channels * mult
                if ds in attention_resolutions:
                    layers.append(AttentionBlock(ch, num_heads=num_heads))
                if level and i == num_res_blocks:
                    layers.append(Upsample(ch, conv_resample))
                    ds //= 2
                self.up_blocks.append(TimestepEmbedSequential(*layers))
        self.out = nn.Sequential(
            norm_layer(ch),
            nn.SiLU(),
            nn.Conv2d(model_channels, out_channels, kernel_size=3, padding=1),
    def forward(self, x, timesteps):
        Apply the model to an input batch.
        :param x: an [N x C x H x W] Tensor of inputs.
        :param timesteps: a 1-D batch of timesteps.
        :return: an [N x C x ...] Tensor of outputs.
        hs = []
        # time step embedding
        emb = self.time_embed(timestep_embedding(timesteps, self.model_channels))
        # down stage
        h = x
        for module in self.down_blocks:
            h = module(h, emb)
            hs.append(h)
        # middle stage
        h = self.middle_block(h, emb)
        # up stage
        for module in self.up_blocks:
            cat_in = torch.cat([h, hs.pop()], dim=1)
            h = module(cat_in, emb)
        return self.out(h)

对于扩散过程，其主要的参数就是timesteps和noise schedule，DDPM采用范围为[0.0001, 0.02]的线性noise schedule，其默认采用的总扩散步数为 1000 。

# beta schedule
def linear_beta_schedule(timesteps):
    scale = 1000 / timesteps
    beta_start = scale * 0.0001
    beta_end = scale * 0.02
    return torch.linspace(beta_start, beta_end, timesteps, dtype=torch.float64)

我们定义个扩散模型，它主要要提前根据设计的noise schedule来计算一些系数，并实现一些扩散过程和生成过程：

class GaussianDiffusion:
    def __init__(
        self,
        timesteps=1000,
        beta_schedule='linear'
        self.timesteps = timesteps
        if beta_schedule == 'linear':
            betas = linear_beta_schedule(timesteps)
        elif beta_schedule == 'cosine':
            betas = cosine_beta_schedule(timesteps)
        else:
            raise ValueError(f'unknown beta schedule {beta_schedule}')
        self.betas = betas
        self.alphas = 1. - self.betas
        self.alphas_cumprod = torch.cumprod(self.alphas, axis=0)
        self.alphas_cumprod_prev = F.pad(self.alphas_cumprod[:-1], (1, 0), value=1.)
        # calculations for diffusion q(x_t | x_{t-1}) and others
        self.sqrt_alphas_cumprod = torch.sqrt(self.alphas_cumprod)
        self.sqrt_one_minus_alphas_cumprod = torch.sqrt(1.0 - self.alphas_cumprod)
        self.log_one_minus_alphas_cumprod = torch.log(1.0 - self.alphas_cumprod)
        self.sqrt_recip_alphas_cumprod = torch.sqrt(1.0 / self.alphas_cumprod)
        self.sqrt_recipm1_alphas_cumprod = torch.sqrt(1.0 / self.alphas_cumprod - 1)
        # calculations for posterior q(x_{t-1} | x_t, x_0)
        self.posterior_variance = (
            self.betas * (1.0 - self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
        # below: log calculation clipped because the posterior variance is 0 at the beginning
        # of the diffusion chain
        self.posterior_log_variance_clipped = torch.log(self.posterior_variance.clamp(min =1e-20))
        self.posterior_mean_coef1 = (
            self.betas * torch.sqrt(self.alphas_cumprod_prev) / (1.0 - self.alphas_cumprod)
        self.posterior_mean_coef2 = (
            (1.0 - self.alphas_cumprod_prev)
            * torch.sqrt(self.alphas)
            / (1.0 - self.alphas_cumprod)
    # get the param of given timestep t
    def _extract(self, a, t, x_shape):
        batch_size = t.shape[0]
        out = a.to(t.device).gather(0, t).float()
        out = out.reshape(batch_size, *((1,) * (len(x_shape) - 1)))
        return out
    # forward diffusion (using the nice property): q(x_t | x_0)
    def q_sample(self, x_start, t, noise=None):
        if noise is None:
            noise = torch.randn_like(x_start)
        sqrt_alphas_cumprod_t = self._extract(self.sqrt_alphas_cumprod, t, x_start.shape)
        sqrt_one_minus_alphas_cumprod_t = self._extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape)
        return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
    # Get the mean and variance of q(x_t | x_0).
    def q_mean_variance(self, x_start, t):
        mean = self._extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start
        variance = self._extract(1.0 - self.alphas_cumprod, t, x_start.shape)
        log_variance = self._extract(self.log_one_minus_alphas_cumprod, t, x_start.shape)
        return mean, variance, log_variance
    # Compute the mean and variance of the diffusion posterior: q(x_{t-1} | x_t, x_0)
    def q_posterior_mean_variance(self, x_start, x_t, t):
        posterior_mean = (
            self._extract(self.posterior_mean_coef1, t, x_t.shape) * x_start
            + self._extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
        posterior_variance = self._extract(self.posterior_variance, t, x_t.shape)
        posterior_log_variance_clipped = self._extract(self.posterior_log_variance_clipped, t, x_t.shape)
        return posterior_mean, posterior_variance, posterior_log_variance_clipped
    # compute x_0 from x_t and pred noise: the reverse of `q_sample`
    def predict_start_from_noise(self, x_t, t, noise):
        return (
            self._extract(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
            self._extract(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
    # compute predicted mean and variance of p(x_{t-1} | x_t)
    def p_mean_variance(self, model, x_t, t, clip_denoised=True):
        # predict noise using model
        pred_noise = model(x_t, t)
        # get the predicted x_0: different from the algorithm2 in the paper
        x_recon = self.predict_start_from_noise(x_t, t, pred_noise)
        if clip_denoised:
            x_recon = torch.clamp(x_recon, min=-1., max=1.)
        model_mean, posterior_variance, posterior_log_variance = \
                    self.q_posterior_mean_variance(x_recon, x_t, t)
        return model_mean, posterior_variance, posterior_log_variance
    # denoise_step: sample x_{t-1} from x_t and pred_noise
    @torch.no_grad()
    def p_sample(self, model, x_t, t, clip_denoised=True):
        # predict mean and variance
        model_mean, _, model_log_variance = self.p_mean_variance(model, x_t, t,
                                                    clip_denoised=clip_denoised)
        noise = torch.randn_like(x_t)
        # no noise when t == 0
        nonzero_mask = ((t != 0).float().view(-1, *([1] * (len(x_t.shape) - 1))))
        # compute x_{t-1}
        pred_img = model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise
        return pred_img
    # denoise: reverse diffusion
    @torch.no_grad()
    def p_sample_loop(self, model, shape):
        batch_size = shape[0]
        device = next(model.parameters()).device
        # start from pure noise (for each example in the batch)
        img = torch.randn(shape, device=device)
        imgs = []
        for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
            img = self.p_sample(model, img, torch.full((batch_size,), i, device=device, dtype=torch.long))
            imgs.append(img.cpu().numpy())
        return imgs
    # sample new images
    @torch.no_grad()
    def sample(self, model, image_size, batch_size=8, channels=3):
        return self.p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
    # compute train losses
    def train_losses(self, model, x_start, t):
        # generate random noise
        noise = torch.randn_like(x_start)
        # get x_t
        x_noisy = self.q_sample(x_start, t, noise=noise)
        predicted_noise = model(x_noisy, t)
        loss = F.mse_loss(noise, predicted_noise)
        return loss

其中几个主要的函数总结如下：

q_sample ：实现的从 \mathbf{x}_0 到 \mathbf{x}_t 扩散过程；
q_posterior_mean_variance ：实现的是后验分布的均值和方差的计算公式；
predict_start_from_noise ： q_sample 的逆过程，根据预测的噪音来生成 \mathbf{x}_0 ；
p_mean_variance ：根据预测的噪音来计算 p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 的均值和方差；
p_sample ：单个去噪step；
p_sample_loop ：整个去噪音过程，即生成过程。

扩散模型的训练过程非常简单，如下所示：

# train
epochs = 10
for epoch in range(epochs):
    for step, (images, labels) in enumerate(train_loader):
        optimizer.zero_grad()
        batch_size = images.shape[0]
        images = images.to(device)
        # sample t uniformally for every example in the batch
        t = torch.randint(0, timesteps, (batch_size,), device=device).long()
        loss = gaussian_diffusion.train_losses(model, images, t)