多变量时间序列的多步预测——LSTM模型
20210918,附上了数据链接,供大家下载。(抱歉,之前的链接因为整理网盘不小心删除了数据...)
链接: https:// pan.baidu.com/s/1T-QSY6 pDSf9tW4EIBO0PeA
提取码:iuwb
-----------------------------------------------------------------------------------------------
一、问题背景
现实生活中,在一系列时间点上观测数据是司空见惯的活动,在农业、商业、气象军事和医疗等研究领域都包含大量的时间序列数据。时间序列的预测指的是基于序列的历史数据,以及可能对结果产生影响的其他相关序列,对序列未来的可能取值做出预测。现实生活中的时间序列数据预测问题有很多,包括语音分析、噪声消除以及股票期货市场的分析等,其本质主要是根据前T个时刻的观测数据推算出T+1时刻的时间序列的值。
那么面对时间序列的预测问题,我们可以用传统的ARIMA模型,也可以用基于时间序列分解的STL模型或者Facebook开源的Prophet模型。在机器学习或者人工智能大热的现在,深度学习等机器学习方法也可以用于时间序列的预测。今天介绍的就是如何基于Keras和Python,实现时间序列的LSTM模型预测。
二、LSTM模型介绍
长短时记忆网络(Long Short Term Memory,简称LSTM)模型,本质上是一种特定形式的循环神经网络(Recurrent Neural Network,简称RNN)。LSTM模型在RNN模型的基础上通过增加门限(Gates)来解决RNN短期记忆的问题,使得循环神经网络能够真正有效地利用长距离的时序信息。LSTM在RNN的基础结构上增加了输入门限(Input Gate)、输出门限(Output Gate)、遗忘门限(Forget Gate)3个逻辑控制单元,且各自连接到了一个乘法元件上(见图1),通过设定神经网络的记忆单元与其他部分连接的边缘处的权值控制信息流的输入、输出以及细胞单元(Memory cell)的状态。其具体结构如下图所示。

上图中相关部件的描述如下:
Input Gate:控制信息是否流入Memory cell中,记为 i_t 。
Forget Gate:控制上一时刻Memory cell中的信息是否积累到当前时刻Memory cell中,记为 f_t 。
Output Gate:控制当前时刻Memory cell中的信息是否流入当前隐藏状态 h_t 中,记为 o_t 。
cell:记忆单元,表示神经元状态的记忆,使得LSTM单元有保存、读取、重置和更新长距离历史信息的能力,记为 c_t 。
在t时刻,LSTM神经网络定义的公式如下:
\begin{array}{l} f_{t}=\operatorname{sigmoid}\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) \\ i_{t}=\operatorname{sigmoid}\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) \\ o_{t}=\operatorname{sigmoid}\left(W_{o} \cdot\left[h_{t-1}, x_{t}\right]+b_{o}\right) \\ \tilde{c}_{t}=\tanh \left(W_{c} \cdot\left[h_{t-1}, x_{t}\right]+b_{c}\right) \\ c_{t}=f_{t} \times c_{t-1}+i_{t} * \tilde{c}_{t} \\ h_{t}=o_{t} \times \tanh \left(c_{t}\right) \end{array} \\
除了前文提及的 i_t 、 f_t 、 o_t 和 c_t , W_* 分别代表其相应门限的递归连接权重,sigmoid和tanh为两种激活函数。
隐藏层cell结构图如图2所示。在LSTM神经网络的训练过程中,首先将t时刻的数据特征输入至输入层,经过激励函数输出结果。将输出结果、t-1时刻的隐藏层输出和t-1时刻cell单元存储的信息输入LSTM结构的节点中,通过Input Gate,Output Gate,Forget Gate和cell单元的处理,输出数据到下一隐藏层或输出层,输出LSTM结构节点的结果到输出层神经元,计算反向传播误差,更新各个权值。

三、LSTM模型准备
3.1 加载需要的包
from math import sqrt
from numpy import concatenate
from matplotlib import pyplot
from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
import pandas as pd
import numpy as np3.2 定义将时间序列预测问题转化为监督学习问题的函数
前文已经提及,时间序列预测的本质主要是根据前T个时刻的观测数据推算出T+1时刻的时间序列的值。这就转化为机器学习中的监督学习问题,输入值为历史值,输出值为预测值。因此,利用LSTM模型进行时间序列预测的第一步便是将数据集整理成监督学习中常见的数据类型,一行为一个样本,行数为样本数,列数为变量总数。这里利用的是pandas库中dataframe的shift函数。
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = [], []
#i: n_in, n_in-1, ..., 1,为滞后期数
#分别代表t-n_in, ... ,t-1期
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
#i: 0, 1, ..., n_out-1,为超前预测的期数
#分别代表t,t+1, ... ,t+n_out-1期
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
agg = concat(cols, axis=1)
agg.columns = names
if dropnan:
agg.dropna(inplace=True)
return agg3.3 定义准备数据的函数
def prepare_data(filepath, n_in, n_out=30, n_vars=4, train_proportion=0.8):
#读取数据集
dataset = read_csv(filepath, encoding='utf-8')
#设置时间戳索引
dataset['日期'] = pd.to_datetime(dataset['日期'])
dataset.set_index("日期", inplace=True)
values = dataset.values
#保证所有数据都是float32类型
values = values.astype('float32')
#变量归一化
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
#将时间序列问题转化为监督学习问题
reframed = series_to_supervised(scaled, n_in, n_out)
#取出保留的变量
contain_vars = []
for i in range(1, n_in+1):
contain_vars += [('var%d(t-%d)' % (j, i)) for j in range(1,n_vars+1)]
data = reframed [ contain_vars + ['var1(t)'] + [('var1(t+%d)' % (j)) for j in range(1,n_out)]]
#修改列名
col_names = ['Y', 'X1', 'X2', 'X3']
contain_vars = []
for i in range(n_vars):
contain_vars += [('%s(t-%d)' % (col_names[i], j)) for j in range(1,n_in+1)]
data.columns = contain_vars + ['Y(t)'] + [('Y(t+%d)' % (j)) for j in range(1,n_out)]
#分隔数据集,分为训练集和测试集
values = data.values
n_train = round(data.shape[0]*train_proportion)
train = values[:n_train, :]
test = values[n_train:, :]
#分隔输入X和输出y
train_X, train_y = train[:, :n_in*n_vars], train[:, n_in*n_vars:]
test_X, test_y = test[:, :n_in*n_vars], test[:, n_in*n_vars:]
#将输入X改造为LSTM的输入格式,即[samples,timesteps,features]
train_X = train_X.reshape((train_X.shape[0], n_in, n_vars))
test_X = test_X.reshape((test_X.shape[0], n_in, n_vars))
return scaler, data, train_X, train_y, test_X, test_y, dataset3.4 定义拟合LSTM模型的函数
def fit_lstm(data_prepare, n_neurons=50, n_batch=72, n_epoch=100, loss='mae', optimizer='adam', repeats=1):
train_X = data_prepare[2]
train_y = data_prepare[3]
test_X = data_prepare[4]
test_y = data_prepare[5]
model_list = []
for i in range(repeats):
#设计神经网络
model = Sequential()
model.add(LSTM(n_neurons, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(train_y.shape[1]))
model.compile(loss=loss, optimizer=optimizer)
#拟合神经网络
history = model.fit(train_X, train_y, epochs=n_epoch, batch_size=n_batch, validation_data=(test_X, test_y), verbose=0, shuffle=False)
#画出学习过程
p1 = pyplot.plot(history.history['loss'], color='blue', label='train')
p2 = pyplot.plot(history.history['val_loss'], color='yellow',label='test')
#保存model
model_list.append(model)
pyplot.legend(["train","test"])
pyplot.show()
return model_list3.5 定义预测的函数
def lstm_predict(model, data_prepare):
scaler = data_prepare[0]
test_X = data_prepare[4]
test_y = data_prepare[5]
#做出预测
yhat = model.predict(test_X)
#将测试集上的预测值还原为原来的数据维度
scale_new = MinMaxScaler()
scale_new.min_, scale_new.scale_ = scaler.min_[0], scaler.scale_[0]
inv_yhat = scale_new.inverse_transform(yhat)
#将测试集上的实际值还原为原来的数据维度
inv_y = scale_new.inverse_transform(test_y)
return inv_yhat, inv_y3.6 定义预测评价的函数(RMSE)
# 计算每一步预测的RMSE
def evaluate_forecasts(test, forecasts, n_out):
rmse_dic = {}
for i in range(n_out):
actual = [float(row[i]) for row in test]
predicted = [float(forecast[i]) for forecast in forecasts]
rmse = sqrt(mean_squared_error(actual, predicted))
rmse_dic['t+' + str(i+1) + ' RMSE'] = rmse
return rmse_dic3.7 定义将预测可视化的函数
#以原始数据为背景画出预测数据
def plot_forecasts(series, forecasts):
#用蓝色画出原始数据集
pyplot.plot(series.values)
n_seq = len(forecasts[0])
#用红色画出预测值
for i in range(1,len(forecasts)+1):
xaxis = [x for x in range(i, i+n_seq+1)]
yaxis = [float(series.iloc[i-1,0])] + list(forecasts[i-1])
pyplot.plot(xaxis, yaxis, color='red')
#展示图像
pyplot.show()四、建立LSTM模型
4.1 建立模型(n_in = 15,n_neuron = 5,n_batch = 16,n_epoch = 200)
为了减少随机性,重复建立五次模型,取五次结果的平均作为最后的预测。
#定义需要的变量
filepath = r'C:\Users\87689\Desktop\国贸实习\Premium\导出文件.csv'
n_in = 15
n_out = 30
n_vars = 4
n_neuron = 5
n_batch = 16
n_epoch = 200
repeats = 5
inv_yhat_list = []
inv_y_list = []
data_prepare = prepare_data(filepath,n_in, n_out)
scaler, data, train_X, train_y, test_X, test_y, dataset = data_prepare
model_list = fit_lstm(data_prepare, n_neuron, n_batch, n_epoch,repeats=repeats)
for i in range(len(model_list)):
model = model_list[i]
inv_yhat = lstm_predict(model, data_prepare)[0]
inv_y = lstm_predict(model, data_prepare)[1]
inv_yhat_list.append(inv_yhat)
inv_y_list.append(inv_y)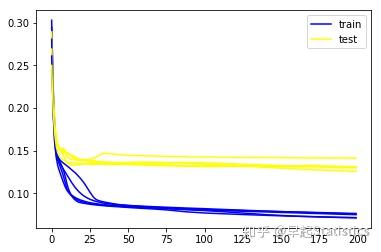
求出平均预测结果
inv_yhat_ave = np.zeros(inv_y.shape)
for i in range(repeats):
inv_yhat_ave += inv_yhat_list[i]
inv_yhat_ave = inv_yhat_ave/repeats4.2 模型评价
求出五次预测结果inv_yhat及最终平均预测结果inv_yhat_ave的每步预测RMSE
rmse_dic_list = []
for i in range(len(model_list)):
inv_yhat = inv_yhat_list[i]
inv_y = inv_y_list[i]
rmse_dic = evaluate_forecasts(inv_y, inv_yhat, n_out)
rmse_dic_list.append(rmse_dic)
rmse_dic_list.append(evaluate_forecasts(inv_y, inv_yhat_ave, n_out))
df_dic = {}
for i in range(len(rmse_dic_list) - 1):
df_dic['第' + str(i+1) + '次'] = pd.Series(rmse_dic_list[i])
df_dic['平均'] = pd.Series(rmse_dic_list[i+1])
rmse_df = DataFrame(df_dic)
rmse_df表1:预测RMSE结果表

下面求最终平均预测结果inv_yhat_ave的每步预测错误率的平均,平均来看,预测结果会比真实结果偏高。
s = inv_yhat_ave[0].shape
erro_rate = np.zeros(s)
for i in range(len(inv_y)):
erro_rate += inv_yhat_ave[i]/inv_y[i]-1
erro_rate_ave = erro_rate/len(inv_y)
err_df = DataFrame(pd.Series(erro_rate_ave))
err_df.columns = ['平均预测错误率']
err_df.index = ['超前%d步预测' % (i+1) for i in range(n_out)]
err_df表2:按步平均预测错误率结果表

4.3 预测结果可视化
测试集的前十个样本
dataset = data_prepare[6]
test_X = data_prepare[4]
n_real = len(dataset)-len(test_X)-len(inv_yhat_ave[0])
#多画一个
y_real = DataFrame(dataset['Y'][n_real:n_real+10+30])
plot_forecasts(y_real, inv_yhat_ave[0:10])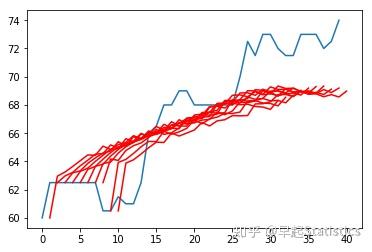
整个测试集
n_real = len(dataset)-len(test_X)-len(inv_yhat[0])
#多画一个
y_real = DataFrame(dataset['Y'][n_real:])
plot_forecasts(y_real, inv_yhat_ave)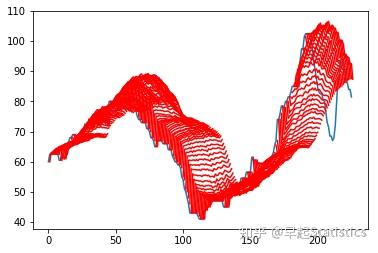
4.4 结果导出
Yhat
pre_df = DataFrame(inv_yhat_ave)
#时间戳处理,让它只显示到日
date_index = dataset.index[n_in-1+len(train_X)-1:n_in-1+len(train_X)+len(test_X)-1]
pydate_array = date_index.to_pydatetime()
date_only_array = np.vectorize(lambda s: s.strftime('%Y-%m-%d'))(pydate_array )
date_only_series = pd.Series(date_only_array)
pre_df = pre_df.set_index(date_only_series)
names_columns = ['未来%d期' % (i+1) for i in range(n_out)]
pre_df.columns = names_columns
pre_df = pre_df.round(decimals=2)#小数点Y
actual_df = DataFrame(inv_y)
names_columns = ['未来%d期' % (i+1) for i in range(n_out)]
