37 个回答
核心还是因为搞工程的比搞理论的人多!
你说说搞通信,搞雷达,控制论不用matlab用啥?
工程上大部分采集数据调试个串口,udp,tcpip协议,mathematica也没matlab方便啊
跟fpga dsp对接,各种数据截位,搞理论的会考虑这种事情吗?用matlab仿真量化噪声,截位确实方便。
mathematica优势 → 理论 → 人少
matlab优势 → 工程→ 人多
认了吧,各位答主别挣扎了,人多欺负人少!
工具就是工具,不要有优越感,尤其是隔壁答案,什么
越好的学校用mathematica的越多
这种回答,以此论证自己用这个比别人优秀?
工具就是工具,有其特定的场景,有适合的适用范围就是好东西!
两者都是非常不错的软件,我都喜欢,人数多少并不能表明软件优劣!

一些人连入门级的问题都搞不定就出来误导别人

都2021了,很多人还是对Mathematica的偏见停留到凭空捏造的印象上。
Matlab本身并没有 符号计算 的能力,目前使用的是Mupad引擎算是二流水平,解不了的 方程 、算不了的 积分 太多了。
用 Matlab 的 solve 解方程要得到解析解,为什么只返回了一个数值解?
定/不定积分
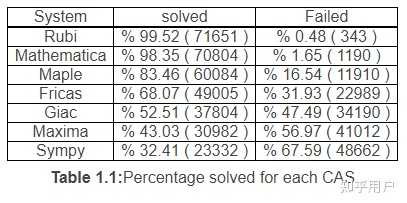
专业的CAS评测没Matlab什么事,最多和Sympy差不多
https://www. 12000.org/my_notes/CAS_ integration_tests/reports/rubi_4_16_1_graded/inch1.htm#x2-10001
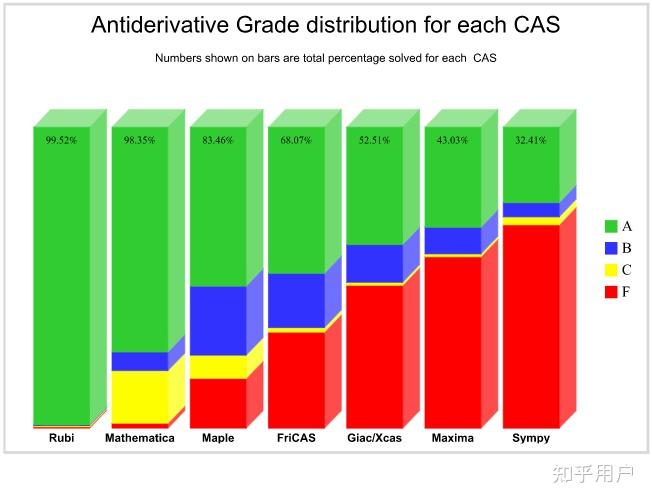
很多人说Matlab的 数值计算 比Mathematica强的多,所以就更流行,到底强在哪里呢?
大多是道听途说,其实未必真的了解,不信你让他们找几个具体的例子看看。
Talk is cheap show me the code.
Matlab的矩阵计算还是不错的,不过现在优势也不大了,Mathematica底层也是链接到MKL,速度上并不会差多少,有时Mathematica反而更快。
不限语言,不用GPU,尽量不并行,计算exp(X)最快的程序应该怎么写?
大家用Mathematica或Matlab不就是馋他们的库函数嘛,不然其他语言那么多都不香吗?
数值积分、非线性方程数值解、数值最优化、微分方程数值解等方面,Matlab的表现只能说很一般,并没有一些人想象的那么好。
- Matlab的大数计算不方便,速度慢
Project Euler上的程序语言排行为什么Matlab比Python低那么多?
- 数值积分
Matlab不擅长高振荡函数的数值积分
高振荡函数的数值积分 – MATLAB中文论坛 (ilovematlab.cn)
三重积分计算一个几何体的体积,Matlab算得很慢,而且得到的结果精度不太好,改method也不好使
f = @(x,y,z)(x.^2 + y.^2 + (z-sqrt(3/8)).^2 < 1) .* ((x+1/sqrt(12)).^2 + (y+1/2).^2 + (z+1/sqrt(24)).^2 < 1) .* ((x+1/sqrt(12)).^2 + (y-1/2).^2 + (z+1/sqrt(24)).^2 < 1) .* ((x-1/sqrt(3)).^2+y.^2+(z+1/sqrt(24)).^2<1);
integral3(f, -inf, inf, -inf, inf, -inf, inf)Mathematica秒出,而且精度更高。很多人把符号计算和数值计算孤立开来,Mathematica之所以表现更好就是因为用符号计算做了一些预处理
NIntegrate[Boole[x^2+y^2+(z-Sqrt[3/2]/2)^2<1&&(x+1/(2 Sqrt[3]))^2+(y+1/2)^2+(z+1/(2 Sqrt[6]))^2<1&&(x+1/(2 Sqrt[3]))^2+(y-1/2)^2+(z+1/(2 Sqrt[6]))^2<1&&(x-1/Sqrt[3])^2+y^2+(z+1/(2 Sqrt[6]))^2<1],{x,-∞,∞},{y,-∞,∞},{z,-∞,∞}]//AbsoluteTiming
- 非线性方程组的数值解
Matlab算了很久只返回了一组解
syms a b d
eqn1=[-31250*(-1+sqrt(sym(3)))^2+(-a+b)^2+(a+b)^2-(2*(-a+b))*(a+b)*cos((1/9)*sym(pi)),
62500+b^2-(-a+d)^2-500*b*cos(2*sym(pi)*(1/9)),
3906250000+a^4-125000*b^2+b^4-62500*sqrt(sym(3))*d^2-2*b^2*d^2+d^4+a^2*(30*b^2-125000+16*sqrt(sym(3))*b^2-2*d^2)];
sol1=vpasolve(eqn1,[a,b,d])
syms x1 x2 y1 y2 k
eqn2=[(-1)+x1.^4+k.*y1.^4,
(-1)+x2.^4+k.*y2.^4,
(-1)+(1/256).*(x1+(-1).* 5.^(1/2).*x1+(3+5.^(1/2)).*x2+(2.*(5+5.^(1/2))).^(1/2).*(y1+(-1).* y2)).^4+(1/256).*k.*((2.*(5+5.^(1/2))).^(1/2).*((-1).*x1+x2)+y1+( -1).*5.^(1/2).*y1+(3+5.^(1/2)).*y2).^4,
(-1)+(1/16).*(x1+x2+(5+2.* 5.^(1/2)).^(1/2).*(y1+(-1).*y2)).^4+(1/16).*k.*((5+2.*5.^(1/2)).^( 1/2).*((-1).*x1+x2)+y1+y2).^4,
(-1)+(1/256).*((3+5.^(1/2)).*x1+x2+( -1).*5.^(1/2).*x2+(2.*(5+5.^(1/2))).^(1/2).*(y1+(-1).*y2)).^4+( 1/256).*k.*((2.*(5+5.^(1/2))).^(1/2).*((-1).*x1+x2)+(3+5.^(1/2)).* y1+y2+(-1).*5.^(1/2).*y2).^4];
sol2=vpasolve(eqn2,[x1,x2,y1,y2,k])Mathematica可以很快算出所有的解
eqn1={
-31250 (-1+Sqrt[3])^2+(-a+b)^2+(a+b)^2-2 (-a+b) (a+b) Cos[Pi/9],
62500+b^2-(-a+d)^2-500 b Cos[(2 Pi)/9],
3906250000+a^4-125000 b^2+b^4-62500 Sqrt[3] d^2-2 b^2 d^2+d^4+a^2 (-125000+30 b^2+16 Sqrt[3] b^2-2 d^2)
sol1=NSolve[eqn1,{a,b,d}];
eqn2={
-1+x1^4+k y1^4,

