因果推断笔记——python 倾向性匹配PSM实现示例（三）

在rubin的理论下， 在观测数据下，为了给实验组寻找合适的对照组，或者消除对照组的影响，有非常多种方式，其中包括：

• - Matching（找对照组）
• - Propensity Score Based Methods（PS中介变量过度）
• - PS Matching ，能解决在高维数据中难以找到相似样本的问题
• - Inverse of Propensity Weighting 方法（IPW）
• - Doubly Robust
• - Directly Confounder Balancing（直接对样本权重进行学习）
• - Entrophy Balancing 方法之中，通过学习样本权重，使特征变量的分布在一阶矩上一致，同时还约束了权重的熵（Entropy）
• - Approximate Residual Balancing。第一步也是通过计算样本权重使得一阶矩一致，第二步与 Doubly Robust 的思想一致，加入了回归模型，并在第三步结合了前两步的结果估计平均因果效应。

0.1 Matching

大牛论文：

0.2 Propensity Score Based Methods

关于PS： Rubin 证明了在给定倾向指数的情况下，Unconfounderness 假设就可以满足。倾向指数其实概括了群体的特征变量，如果两个群体的倾向指数相同，那他们的干预变量就是与其他特征变量相独立的。

0.2.1 PSM

其中PS的方式也可以与Matching进行结合，也就是PSM； 做 Matching，这样能解决在高维数据中难以找到相似样本的问题

0.2.2 IPW

Inverse of Propensity Weighting 方法，对于干预变量为1的样本使用倾向指数的倒数进行加权，而对于为0的样本使用（1-倾向指数）的倒数进行加权，两类样本的加权平均值之差就是平均因果效应的大小。 这里有一个假设，就是估计出的倾向指数与真实的倾向指数是相等的。

因此这个方法有两个弱点， - 一是需要对倾向指数的估计足够精确 - 二是如果倾向指数过于趋近0或1，就会导致某些权重的值过高，使估计出的平均因果效应的方差过大。

其他关联可见：

经过IPW加权之后，我们大致认为各组样本之间不存在选择性偏差，这时，我们用对照组的观测结果的加权值来估计整体的对照策略的潜在结果期望，用试验组的观测结果的加权值来估计整体的试验策略的潜在结果期望。

0.2.3 Doubly Robust

IPW需要样本权重主要围绕倾向的分为核心，倾向得分一旦预测不准，会导致上面的估计方法出现很大的偏差。

为了解决样本权重过度依赖倾向得分准确性的问题， 大佬又提出了Doubly Robust estimator (DR)方法或者成为增强IPW(AIPW)。 DR方法具体做法类似于鸡蛋不放在一个篮子里的投资方法，它结合倾向得分和结果回归模型来得到样本权重，其具体做法如下：

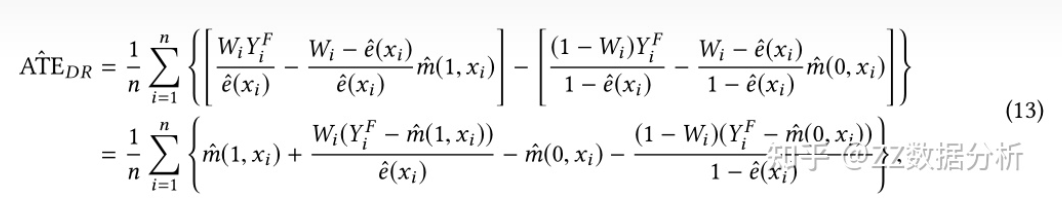
这个方法需要根据已有数据，再学习一个预测的模型，反事实评估某个个体在干预变量变化后，结果变量的期望值。 只要倾向指数的估计模型和反事实预测模型中有一个是对的，计算出的平均因果效应就是无偏的； 但如果两个模型估计都是错误的，那产生的误差可能会非常大。

0.2.4 Covariate balancing propensity score (CBPS)

IPW方法的倾向得分其实是策略的倾向选择概率，但是选择性偏差带来的是样本之间其他相关变量分布的不平衡。所以使用逆倾向得分属于只考虑了策略的倾向选择概率，却用来平衡样本之间其他相关变量的分布。Covariate balancing propensity score (CBPS)，协变量平衡倾向得分方法被设计出来来同时衡量这两方面，来使倾向得分更准确。CBPS得到倾向得分的方式是求解下面的方程：

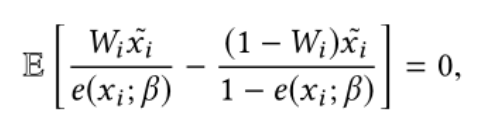
0.2.5 数据驱动的变量分解算法（D²VD）

以上的这三种基于倾向指数的方法比较粗暴，把干预变量和结果变量之外的所有变量都当作混淆变量。而在高维数据中，我们需要精准地找出那些真正需要控制的混淆变量。我们提出了一种数据驱动的变量分解算法（D²VD），将干预变量和结果变量之外的其他变量分为了三类：

1. 混淆变量（Confounders）：既会影响到干预变量，还会影响到结果变量
   
2. 调整变量（Adjustment Variables）：与干预变量独立，但会影响到结果变量
   
3. 无关变量：不会直接影响到干预变量与结果变量
   

进行分类之后，就可以只用混淆变量集去估计倾向指数。而调整变量集会被视为对结果变量的噪声，进行消减。最后使用经过调整的结果，去估计平均因果效应。我们从理论上证明了，使用这种方法可以得到无偏的平均因果效应估计，而且估计结果的方差不会大于 Inverse of Propensity Weighting 方法。

0.3 Directly Confounder Balancing

直接对样本权重进行学习。 这类方法的动机就是去控制在干预变量下其他特征变量的分布。 上述的样本加权方法可以在将观测到样本其他变量均视为混杂因素的意义上实现平衡。 然而，在实际情况中，并非所有观察到的变量都是混杂因素。有些变量被称为调整变量，只是对结果有影响，还有一些可能是无关的变量。

0.3.1 Entrophy Balancing

方法之中，通过学习样本权重，使特征变量的分布在一阶矩上一致，同时还约束了权重的熵（Entropy）。但这个方法的问题也是将所有变量都同等对待了，把过多变量考虑为混杂变量。

0.3.2 Approximate Residual Balancing

第一步也是通过计算样本权重使得一阶矩一致，第二步与 Doubly Robust 的思想一致，加入了回归模型，并在第三步结合了前两步的结果估计平均因果效应。只要样本权重的估计和反事实预测模型中有一个是对的，计算出的平均因果效应就是无偏的。但这里也是将所有变量都同等对待了。

1 倾向性得分

1.0 ATT与ATE的关系

ATT：参与者平均处理效应（Average Treatment Effect on the Treated，ATT） ATE：全部样本的平均处理效应，Average Treatment Effect，ATE）

随机化试验那部分我们讲到了：

T⊥(Y(1), Y(0))(⊥表示独立性)

这个公式其实包含了较强的可忽略性（Ignorability）假定，但我们之前说了，这种方式比较“贵”，所以通常我们会希望收集足够多的X，使得：

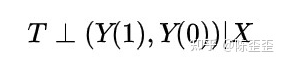
估计ATT最理想的方法是找到参与实验的个体在平行时空的自己，并假设平行时空的自己没有参与实验，最后作差得出最纯粹的ATT，但是找到平行时空的自己不现实； 退而求其次，我们可以使用随机分组的处理组与控制组，作差得到ATT，但现实中个体是否参与实验的选择不随机； 为了得到随机化分组的样本，找出影响个体是否参与实验的因素，控制两组间因素的取值相等，最后利用处理后的分组样本作差得到ATT。

但是，平行时空中的个体一般是无法找到的（至少现在不能~）

为了使 $ATT = ATE$，其中一个思路就是消掉选择偏差这一部分 处理组的选择是随机的，就能实现处理组虚拟变量与结果变量均值独立,只要处理组的选择是随机的，两组间的y之差就是我们需要的参与组平均处理效应ATT

1.1 matching 的讨论

有一篇专门说matching综述论文：

1.1.1 PSM的一些问题

PSM是为了找到实验组比较适配的对照组，之所有会找，大概率是只有观测数据，没有实验数据。 实用性角度，matching 把本来就能一步完成的回归，硬生分作两步：

- 第一步：匹配合适的对照组

- 第二步：用匹配到的对照组和实验组的数据做回归

matching 也无法解决隐形的遗漏变量问题（或内生性问题）。 Matching 是一个有争议的方法，我认识很多老师他们对PSM 包括其它传统的matching是有看法的，觉得有点鸡肋， 原因一是任何matching都是基于一套weighting 规则， 你咋证明这套weighting 规则就比你直接加控制变量进去好？ 原因二是有时候用了matching 也构建不出一个很好的对照组，规则严了找不到好的common support，规则松了对照组和不matching 前也差不了多少。

1.1.2 面板数据中：PSM和DID是天生绝配！

现实中的政策本质上是一种非随机化实验（或称，准自然实验），因此政策效应评估所使用的DID方法难免存在自选择偏差，而使用PSM方法可以为每一个处理组样本匹配到特定的控制组样本，使得准自然实验近似随机，注意是近似，因为影响决策的不可观测因素在两组间仍然存在差异。

PSM - DID也并非是解决选择偏差的灵丹妙药，除了PSM本身不能控制因不可观测因素导致的组间差异，在与DID结合时还存在一个更为关键的问题。

从本质上来说，PSM适用于截面数据，而DID仅仅适用于时间 - 截面的面板数据。

• 对于PSM，每一个处理组样本匹配到的都是同一个时点的控制组样本，相应得到的ATT仅仅是同一个时点上的ATT。下文psmatch2的输出结果中，ATT那一行结果就仅仅代表同一个时点上的参与者平均处理效应。
• 对于DID，由于同时从时间与截面两个维度进行差分，所以DID本身适用的条件就是面板数据。因此，由PSM匹配到的样本原本并不能直接用到DID中做回归。

面对两者适用数据类型的不同，现阶段的文献大致有两种解决思路。

- 第一，将面板数据视为截面数据再匹配。如上文参考文献中的绝大多数。

- 第二，逐期匹配。如，Heyman et al.（2007）[11]、Bockerman & Ilmakunnas（2009）[12]等。

1.1.3 PSM的一些使用条件

1.样本量尽量大，如果样本太小，会导致处理组许多样本在控制组中找不到能匹配的样本，或者能匹配，但是距离很远，也就是控制组的这个样本与处理组的这个样本相对是最匹配的，但是绝对匹配度依然不高。

2.处理组与控制组的倾向得分有较大共同取值范围，否则会丢失较多样本，导致匹配的样本不具备代表性。

需要注意的是，PSM 只能缓解由可观测变量带来的内生性问题，无法处理最为关键的由不可观测变量带来的内生性问题。以上面的例子为例，如果影响企业是否披露R&D投资的因素是不可观测的，那么PSM就不适用了。并且只是缓解，从根本上处理内生性问题还得用IV方法。

1.2 相似性的测度标准

到底多相似（距离、卡尺）算相似呢？标准不同找到的匹配对象就不同。

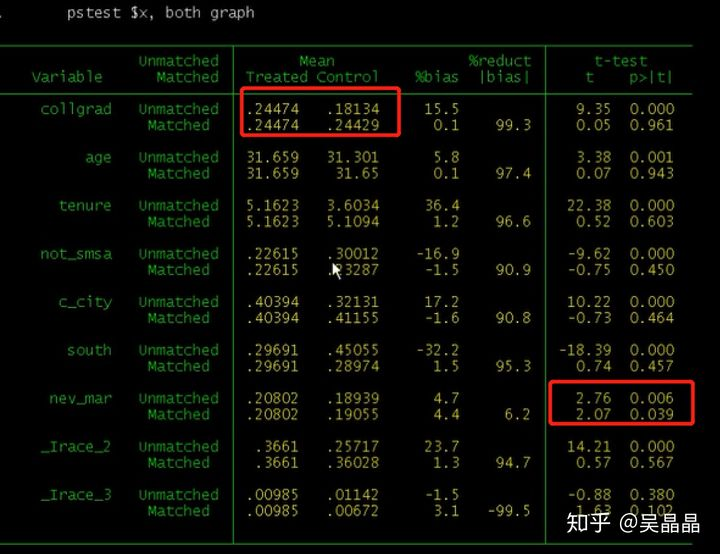
距离。一般的欧式距离、标准化的欧式距离、马氏距离。后两者距离测度方法消除了量纲（or 单位）的影响。下面展示一个标准化欧式距离的公式：

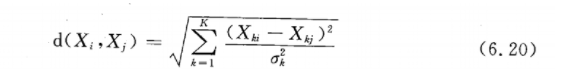
卡尺。根据倾向指数设定卡尺，只有再卡尺范围内，才有可能相似。有卡尺的马氏距离匹配将距离定义为：

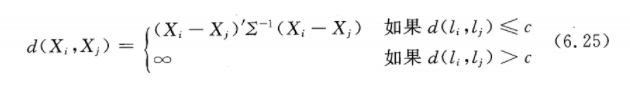
1.3 匹配实施方法

1.3.1 近邻匹配（nearest neighbor matching）

1.3.1.1 1对1匹配

【概念】指为每一个干预组个体在控制组中寻找个距离最近的控制组个体与其匹配（一夫一妻）。

【优缺点】最终的匹配样本比较少,估计方差较大,但每个干预组个体寻找到的都是最近的,因而,偏差比较小。

1.3.1.2 1对多匹配

【概念】为每个干预组个体在控制组寻找多个个体与其匹配（一夫多妻）。

【优缺点】寻找的匹配比较多,匹配样本容量比较大,估计精度提高,但由于一对多近邻匹配中,与干预组个体相匹配的第二个、第三个等后面的控制组个体与干预组个体的相似性下降,从而估计偏差会增加。

权衡后的选择：控制组样本数量很多时,可以考虑一对多近邻匹配。

1.3.2 其他匹配

重复匹配。 重复选择控制组进行匹配能降低匹配偏差，但是会降低最终匹配样本的样本量，估计精度可能下降。

贪婪匹配vs最优匹配。 贪婪匹配（个体最优，整体不一定最优）是指对每一个干预组个体都在控制组中寻找一个距离最近的.但是保证每一对距离最近,对全部干预组个体而言,匹配上的控制组样本并不一定是总体上最近的另一种匹配方法。总体上对所有的干预组个体同时进行匹配,寻找对所有干预组个体而言匹配上的总距离最小。 权衡后的选择：如果关心平均因果效应，选择贪婪匹配即可；如果关心每个个体的匹配效果，最优匹配会得到更为平衡的结果。

raidus matching 半径、近邻匹配

选择一个半径内最接近的样本作为控制组，增大了方差，减少了偏差。

核匹配 kernel and local linear matching 将处理组样本与由控制组所有样本计算出的一个估计效果进行配对，其中估计效果由处理组个体得分值与控制组所有样本得分值加权平均获得，而权数则由核函数计算得出。 这种方法的主要在于选择全部对照组的样本作为对照组，通过给与不同样本不同权重的方式予以控制

分层匹配

根据协变量的取值进行分层。 主要思路在于把样本分为几个子样本，确这几个子样本不存在较大差异，然后在子样本内做均值的回归

1.4 三种常见的Matching方法

• 倾向性评分匹配法(Propensity Score Matching，PSM) PSM将处理组和对照组中倾向性评分接近的样本进行匹配后得到匹配群体，再在匹配群体中计算因果效应。最常用的匹配方法是最近邻匹配法(nearest neighbor matching)，对于每一个处理组的样本，从对照组选取与其倾向评分最接近的所有样本，并从中随机抽取一个或多个作为匹配对象，未匹配上的样本则舍去。
  
• 倾向性评分分层法(Propensity Score Stratification，PSS) PSS将所有样本按照倾向性评分大小分为若干层(通常分为5-10层)，此时层内组间混淆变量的分布可以认为是均衡的，当层内有足够样本量时，可以直接对单个层进行分析，也可以对各层效应进行加权平均。当两组的倾向性评分分布偏离较大时，可能有的层中只有对照组个体，而有的层只有试验组的个体，这些层不参与评估因果效应。PSS的关键问题是分层数和权重的设定。可通过比较层内组间倾向性评分的均衡性来检验所选定的层数是否合理，权重一般由各层样本占总样本量的比例来确定。
  
• 倾向性评分加权法(Propensity Score Weighting，PSW) 一般有两种加权方法：逆概率处理加权法（the inverse probability of treatment weighting，IPTW）和标准化死亡比加权法（the standardized mortality ratio weighting，SMRW）
  

PSW在计算得出倾向性评分的基础上，通过倾向性评分值赋予每个样本一个相应的权重进行加权，使得处理组和对照组中倾向性评分分布一致，从而达到消除混淆变量影响的目的。

2 基于倾向性评分法理论实现步骤

倾向性评分法由Rosenbaum和Rubin于1983年首次提出，是控制混淆变量的常用方法，其基本原理是将多个混淆变量的影响用一个综合的倾向性评分来表示，从而降低了混淆变量的维度。

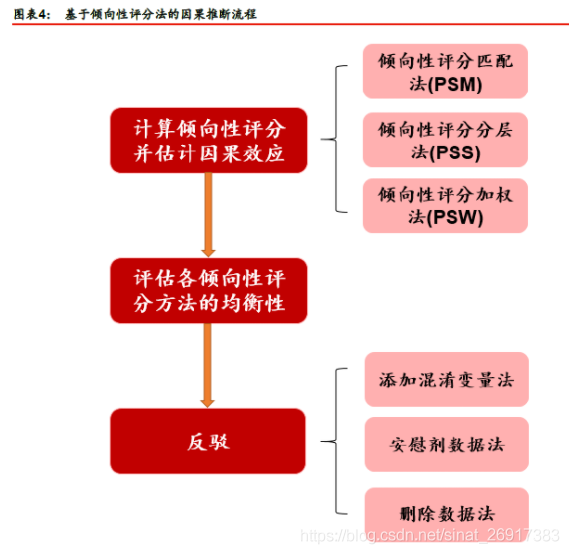
倾向性评分是给定混淆变量W的条件下，个体接受Treatment的概率估计，即 P(T=1|W)。 需要以Treatment为因变量，混淆变量Confounders为自变量，建立回归模型(如Logistic回归)来估计每个研究对象接受Treatment的可能性。

回归：T~W

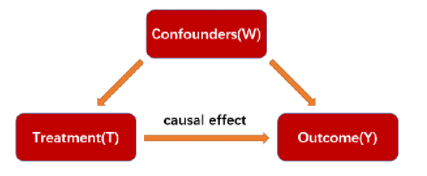
可以分为以下几个步骤：

2.1 选择协变量

计算倾向得分类似于一个降维的过程，把非常多的协变量维度降为一个维度，就是倾向得分，也就是倾向得分综合包含了所有协变量的信息。两个个体的倾向得分非常接近，并不意味着这两个个体的其他属性也接近，这不好判断。不过根据PSM的原理，倾向得分接近就够了，其他属性也接近更好。

协变量太多，则维度太高，找到相似的匹配对象不容易，维度越高越不容易，协变量太少则难以说明个体和匹配对象高度相似。所以协变量的选择需要权衡。

2.2 倾向性得分估算

-倾向性得分估算：倾向性得分怎么估算？

• 因变量为是否被干预Treatment，自变量为用户特征变量。套用LR或者其他更复杂的模型，如LR + LightGBM等模型估算倾向性得分。

2.3 倾向性得分匹配

倾向性得分匹配：怎么用得分完成匹配？

有了每个用户的倾向性得分，针对目前的实验组用户，匹配得到一个接近相同的对照组。 - 1、匹配用的得分：可选原始倾向性得分 e(x) 或者得分的 logit，ln(e(x)/(1−e(x)))。 - 2、修剪（trimming）：先筛选掉倾向性得分比较 “极端” 的用户。常见的做法是保留得分在 [a,b]这个区间的用户，关于区间选择，实验组和对照组用户得分区间的交集，只保留区间中部 90% 或者 95%，如取原始得分在 [0.05,0.95]的用户。 - 3、匹配（matching)：实验组对对照组根据得分进行匹配的时候，比较常见的有以下两种方法。nearest neighbors: 进行 1 对 K 有放回或无放回匹配。 radius: 对每个实验组用户，匹配上所有得分差异小于指定 radius 的用户。 - 4、得分差异上限：当我们匹配用户的时候，我们要求每一对用户的得分差异不超过指定的上限。

2.4 平衡性/均衡性检验检查

平衡性/均衡性检验检查：怎么知道匹配效果？或者实验组、对照组分布是否均匀？

怎么衡量 “配平效果 “呢？比较直观的是看倾向性得分在匹配前后的分布、以及特征在匹配前后的 QQ-Plot。匹配后的实验组和对照组的倾向性得分分布更加接近，变量分布也更接近。量化指标 Standarized Mean Difference (SMD)。SMD 的一种计算方式为：（实验组均值 - 对照组均值）/ 实验组标准差。一般如果一个变量的 SMD 不超过 0.2，一般就可以认为这个变量的配平质量可以接受。当一个变量的 SMD 超过 0.2 的时候，需要凭经验确认一下那个变量是不是没有那么重要。

倾向性评分法要求匹配后样本的所有混淆变量在处理组和对照组达到均衡，否则后续分析会有偏差，因此需要对匹配之后的样本进行均衡性检验。

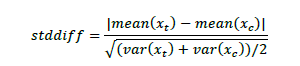
还包括： 共同支撑检验（common support检验）：主要检验的目的是为了确定针对每个处理组，都有对照组与之匹配，一般可以通过倾向匹配得分的分布进行观察，看是否符合，对于没有找到对照组的处理组，去掉其样本 主要对匹配前后的核密度图进行对比，最好的结果是匹配之后两条线很相近。有的时候也会用第二章条形图。

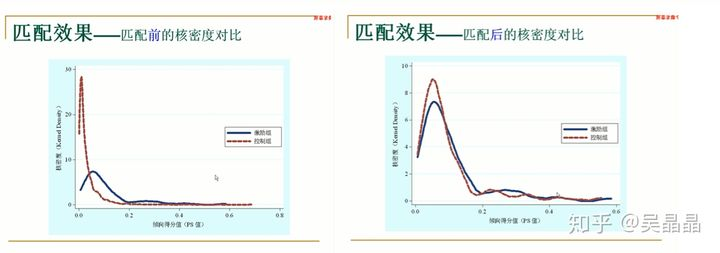
平衡性检验 追求的目标：匹配前后各个变量的均值之间没有明显差异（均值偏差小，t值之小不显著）。主要是下面的表格和图。

2.5 因果效应估算

因果效应估算：匹配后，怎么从匹配后的两组用户中得到因果效应？

我们的目标是推断实验组的平均干预效应 ATT (Average Treatment Effect on the Treated)。ATT 的定义为 ATT=E[Y1−Y0|T=1]。 - 现在我们已经有一对接近同质的实验组和对照组了，有很多方法可以用来估算 ATT 。可以直接比较匹配后的实验组和对照组，也可拟合一个由干预和用户特征预测观察结果的线形模型，看看干预 T 的系数是多少。

看y变量的ATT和显著性，如下图

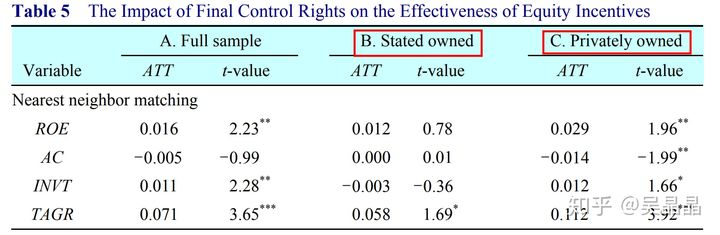
2.6 敏感度分析与反驳

敏感度分析与反驳：混淆变量的选择等主观的一些分析是否会得到一致的分析结论？

敏感性分析主要的目标是衡量当混淆变量（特征）不满足非混淆假设（unconfoundedness ）时，分析结论是不是稳健的。简单的做法是去掉一个或者多个混淆变量重复上面的过程。

反驳(Refute)使用不同的数据干预方式进行检验，以验证倾向性评分法得出的因果效应的有效性。反驳的基本原理是，对原数据进行某种干预之后，对新的数据重新进行因果效应的估计。 理论上，如果处理变量(Treatment)和结果变量(Outcome)之间确实存在因果效应，那么这种因果关系是不会随着环境或者数据的变化而变化的，即新的因果效应估计值与原估计值相差不大。 反驳中进行数据干预的方式有： - 安慰剂数据法：用安慰剂数据(Placebo)代替真实的处理变量，其中Placebo为随机生成的变量或者对原处理变量进行不放回随机抽样产生的变量。 - 添加随机混淆变量法：增加一个随机生成的混淆变量。 - 子集数据法：随机删除一部分数据，新的数据为原数据的一个随机子集。

3 倾向性得分案例解读一（无代码）：就业与收入的影响

Lalonde数据集是因果推断领域的经典数据集 数据集共包含445个观测对象，一个典型的因果推断案例是研究个人是否参加就业培训对1978年实际收入的影响。 treatment变量，就业培训与否0/1 混淆变量为age、educ、black、hisp、married、nodeg。

3.1 第一步:使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表7中，由于不同方法的原理不同，估计的因果效应值也不同。其中倾向性评分匹配法(PSM)因果效应估计值为2196.61，即参加职业培训可以使得一个人的收入增加约2196.61美元 我们计算ATE(Average Treatment Effect)，即在不考虑任何混淆变量的情况下，参加职业培训(treat=1)和不参加职业培训(treat=0)两个群体收入(re78)的平均差异，在不考虑混淆变量下，参加职业培训可以使得一个人的收入增加约1794.34美元。

另外从ATE和几个估计方法的差异来看，ATE 与PSS/PSW差异不大（说明混淆变量影响不大），PSM差异较大，所以可能PSM不太稳定。

3.2 第二步：评估各倾向性评分方法的均衡性

图表8展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小(除了hisp)，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

3.3 第三步：反驳

图表8展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表9最右侧进行对比。 在安慰剂数据法中，由于生成的安慰剂数据(Placebo)替代了真实的处理变量，每个个体接收培训的事实已不存在，因此反驳测试中的因果估计效应大幅下降，接近0，这反过来说明了处理变量对结果变量具有一定因果效应。 在添加随机混淆变量法和子集数据法中，反驳测试结果的均值在1585.19~1681.75之间。

对比真实数据的因果估计效应值，PSM的反驳测试结果大符下降，说明其估计的因果效应不太可靠； PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

所以，可以需要得到的结论： - 需要挑选PSM/PSS/PSW中一个合适的方法 - 然后来看因果是正向还是负向（因果效应估计值的正负）

4 倾向性匹配案例二（无代码）：是否有诊所与死亡率的因果关系

比较清晰了给出了PSM匹配步骤的做法，不过可惜没有代码

对比对照组和实验组项目实施前和项目实施后的新生儿死亡率，进行Difference in Difference 的研究，目前我们假设，并没有历史的新生儿死亡率数据 数据样式：

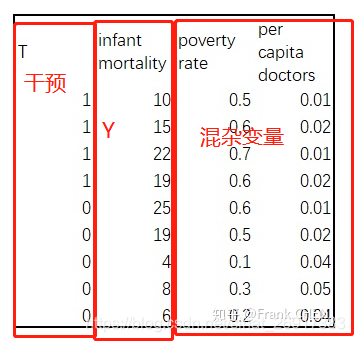
这里把treatment-T（有没有诊所），Outcome - Y（infant mortality 死亡率），都标明了；两个混杂变量，poverty rate 贫穷率 和per capita doctors 人均医生数。

目标：为每一个实验组的村庄创建/找到新的对照组： 针对每一个实验组的村庄，找到其特征类似的对照组。

4.1 PSM Step1：计算Propensity Score

import statsmodels.api as sm
formula = "T ~ poverty_rate + per_capita_doctors"
model = sm.Logit.from_formula(formula, data = data)
re = model.fit()
X = data[['poverty_rate', 'per_capita_doctors']]
data['ps'] = re.predict(X)

这里注意，不是 Y ~ f(T,X) ，而是 T~f(Y,X)

那么最终出来的结果就是， 每个村庄有诊所的可能性。

4.2 PSM Step2：Matching

计算出Propensity Score后，在对照组中需要寻找到与实验组行为（贫穷率、人均医生数）相似的村庄，此过程被称为Matching。 在这里我们采取最简单的临近匹配法，对每一个实验组村庄进行遍历，找到ps值最接近的对照组村庄作为新对照组集合中的元素，即为new_control_index。

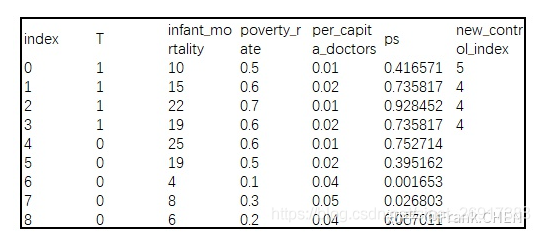
因为我们需要为有诊所的村庄（T = 1） 一一对应找无诊所（T=0）村庄 所以，以index=0的实验组村庄为例（ps=0.416571），在健康诊所项目启动前，与其贫穷率、人均医生数最为接近的对照组成员为index=5村庄（ps=0.395162）。

这里的计算方式就是非常简单的：ps(index=5) - ps(index = 1)是最小

到此为止，每个实验组村庄都找到了其新的对照组归宿~

4.3 PSM Step3：实验组 VS 新对照组 评估建立健康诊所对新生儿死亡率的影响

新对照组村庄（未建立健康诊所）新生儿死亡率比实验组村庄（建立健康诊所）足足高出7%，从而证明这个NGO组织的健康诊所项目对新生儿死亡率的降低有显著作用。

5 倾向性匹配案例（含代码）案例三

整个代码非常简单，抽取 + 参考 文档： psmatching github:

笔者练习代码：

基本实现与案例二无差别，那我们就来看一下。

import psmatching.match as psm
import pytest
path = "simMATCH.csv"
model = "CASE ~ AGE + TOTAL_YRS"
k = "3"
# m = psm.PSMatch(path, model, k)
# Instantiate PSMatch object
m = PSMatch(path, model, k)
# Calculate propensity scores and prepare data for matching
m.prepare_data()
# Perform matching