利用arima预测中国GDP

2 年前

折磨王

利用python从tushare数据库（ID:435525）中读取中国GDP从1992年到2020年的数据。

按照惯例，摒弃2020年的异常GDP数据。下图为1992年第一季度到2019年第四季度中国GDP。

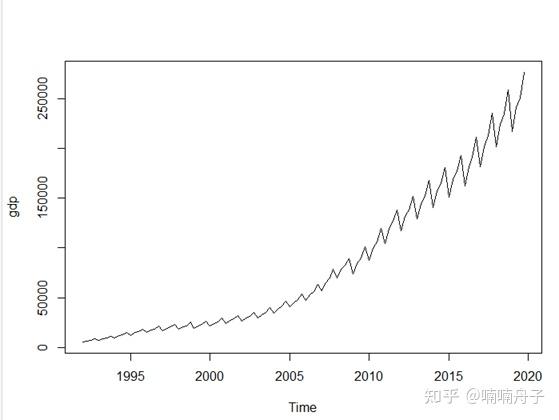
观察到随着时间推进方差变大，故可对数据取对数，如下图。

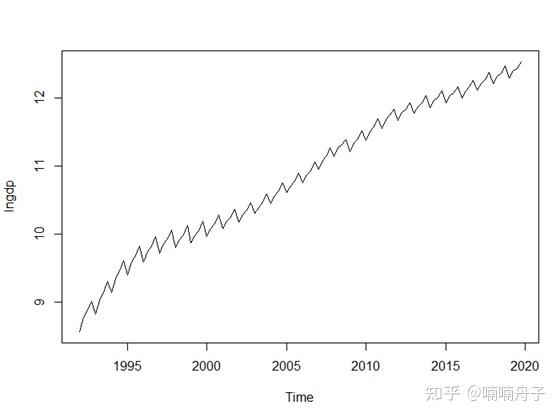
以下分别为中国季度GDP的环比增长率和同比增长率。

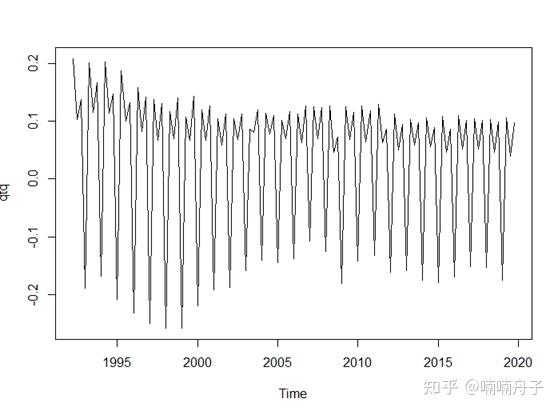
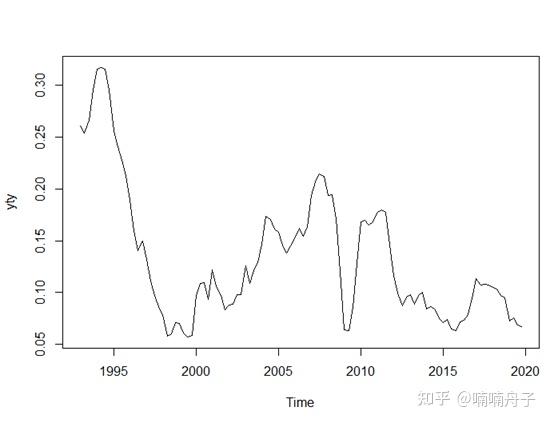
使用decompose函数对环比增长率和GDP对数分解，并去除季节性波动，代码如下。

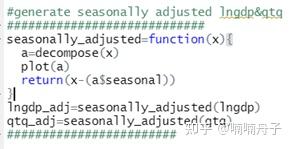
分别得到结果如下图。

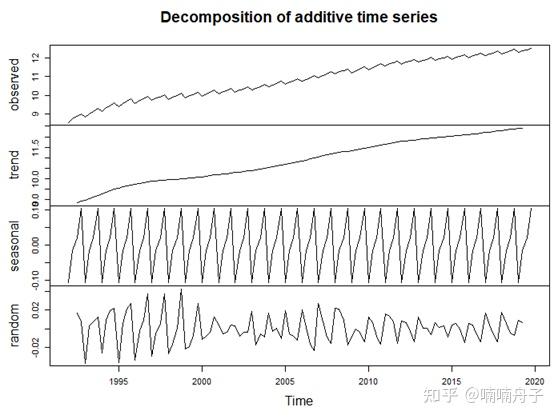
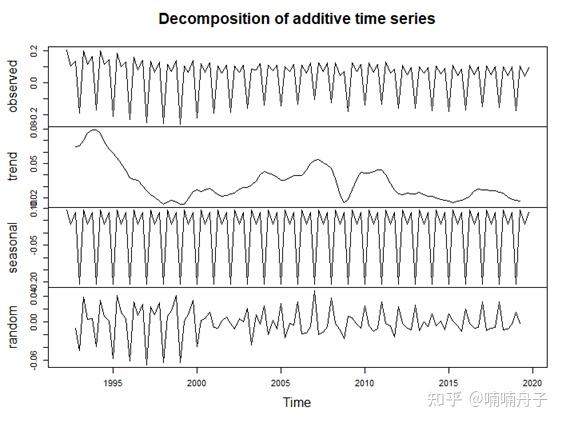
季节调整后的环比增长率和GDP对数如下图。

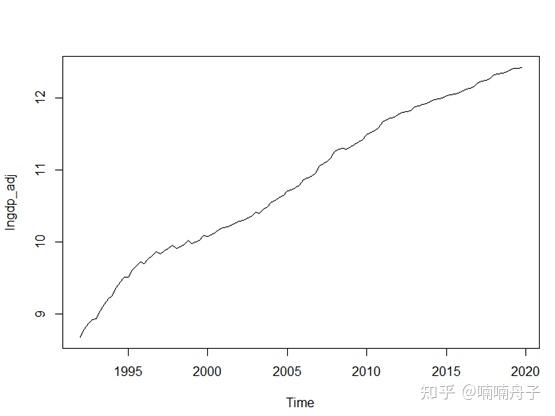
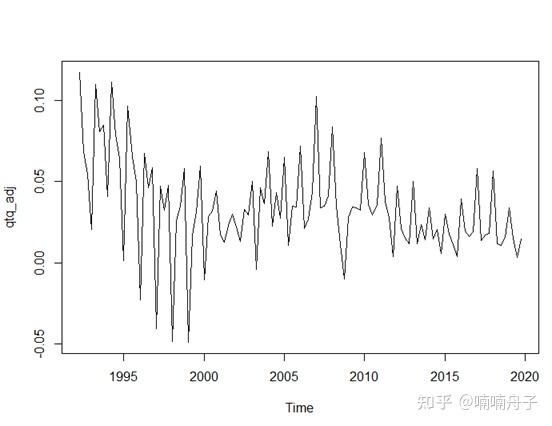
自编了一个滚动用ARIMA方法固定长度窗口作预测的函数。

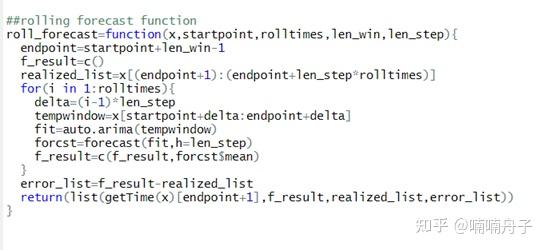
分别做一步预测和两步预测。由于样本大小有限，固定窗口长度为96，滚动五次，调整同比增长率、环比增长率和gdp对数的窗口起点分别为1，4，5使得提前一步预测滚动得到2017Q1到2018Q1的预测值，提前两步预测滚动得到2017Q1到2019Q1的预测值。代码如下。

将得到的同比增长率、季节调整GDP对数、季节调整环比增长率预测值分别还原成GDP的尺度，并得出相应的真实值。代码如下。

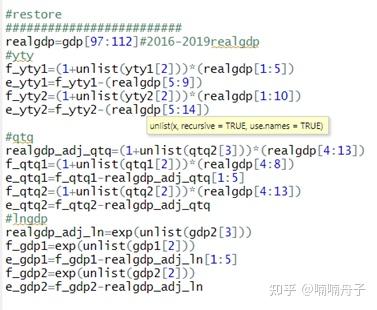
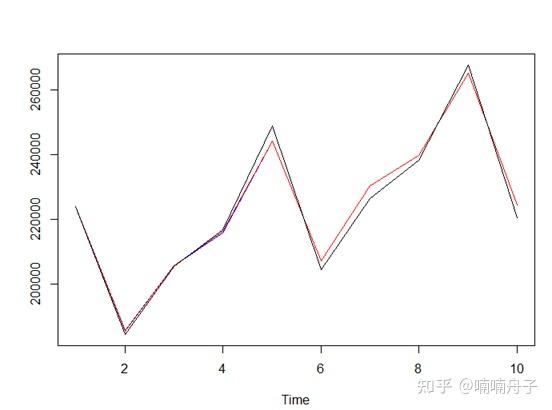
以下蓝线表示提前一步预测的结果，红线表示提前两步的预测结果，黑线表示真实值。

同比增长率预测效果。

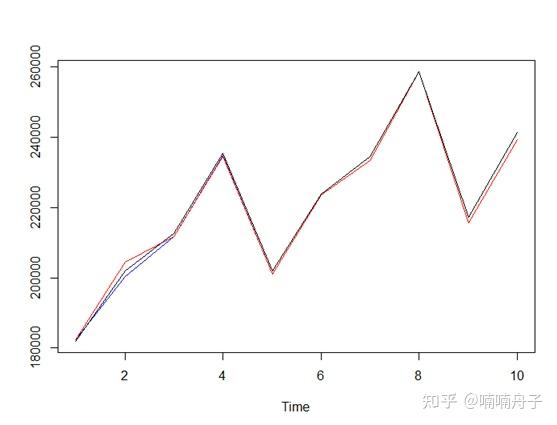
环比增长率预测效果。

对数GDP预测效果。

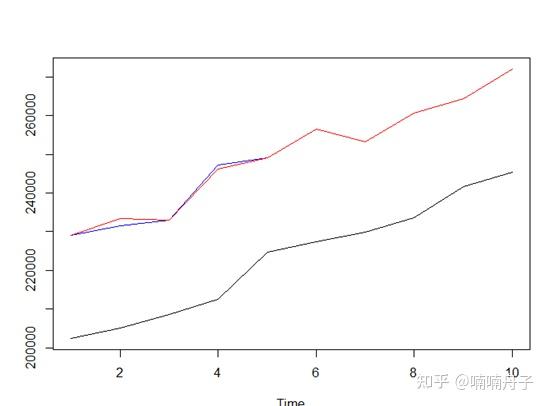
对数GDP的样本外预测偏离明显，精度不好。但是同比增长率和环比增长率预测效果似乎难以区分。

取每种方法预测误差时间序列的原点矩除以误差时间序列的长度，谁大谁则精度相对差。

注意到提前一步预测的同比增长率方法值为234499.6小于环比增长率方法值为1183681，提前两步预测的同比增长率方法值为192927.1小于环比增长率方法值为782947.1。从而可判断同比增长率样本外预测精度更高，同理GDP原始数据方法样本外预测精度最差。

rm(list=ls())
library(readxl)
library(urca)
library(fBasics)
library(forecast)
library(tseries)
df<-read_excel('gdp_cn_quarterly.xlsx')
gdp=ts(df$gdp[1:112],start=c(1992,1),frequency = 4)
lngdp=ts(log(gdp),start=c(1992,1),frequency = 4)
qtq=ts(diff(lngdp,1),start=c(1992,2),frequency = 4)
yty=ts(diff(lngdp,4),start=c(1993,1),frequency = 4)
plot(gdp)
plot(lngdp)
plot(qtq)
plot(yty)
#generate seasonally adjusted lngdp&qtq
############################
seasonally_adjusted=function(x){
  a=decompose(x)
  plot(a)
  return(x-(a$seasonal))
lngdp_adj=seasonally_adjusted(lngdp)
qtq_adj=seasonally_adjusted(qtq)
plot(lngdp_adj)
plot(qtq_adj)
########################
##rolling forecast function
roll_forecast=function(x,startpoint,rolltimes,len_win,len_step){
  endpoint=startpoint+len_win-1
  f_result=c()
  realized_list=x[(endpoint+1):(endpoint+len_step*rolltimes)]
  for(i in 1:rolltimes){
    delta=(i-1)*len_step
    tempwindow=x[startpoint+delta:endpoint+delta]
    fit=auto.arima(tempwindow)
    forcst=forecast(fit,h=len_step)
    f_result=c(f_result,forcst$mean)
  error_list=f_result-realized_list
  return(list(getTime(x)[endpoint+1],f_result,realized_list,error_list))
#one step ahead
#############
yty1=roll_forecast(x=yty,startpoint=1,rolltimes=5,len_win=96,len_step=1)
qtq1=roll_forecast(x=qtq_adj,startpoint=4,rolltimes=5,len_win=96,len_step=1)
gdp1=roll_forecast(x=lngdp_adj,startpoint=5,rolltimes=5,len_win=96,len_step=1)
#two steps ahead
##############
yty2=roll_forecast(x=yty,startpoint=1,rolltimes=5,len_win=96,len_step=2)
qtq2=roll_forecast(x=qtq_adj,startpoint=4,rolltimes=5,len_win=96,len_step=2)
gdp2=roll_forecast(x=lngdp_adj,startpoint=5,rolltimes=5,len_win=96,len_step=2)
f_yty1=exp(unlist(yty1[2]))*(realgdp[1:5])
e_yty1=f_yty1-(realgdp[5:9])
f_yty2=(1+unlist(yty2[2]))*(realgdp[1:10])
e_yty2=f_yty2-(realgdp[5:14])
realgdp_adj_qtq=(1+unlist(qtq2[3]))*(realgdp[4:13])
f_qtq1=(1+unlist(qtq1[2]))*(realgdp[4:8])
e_qtq1=f_qtq1-realgdp_adj_qtq[1:5]
f_qtq2=(1+unlist(qtq2[2]))*(realgdp[4:13])
e_qtq2=f_qtq2-realgdp_adj_qtq
#lngdp
realgdp_adj_ln=exp(unlist(gdp2[3]))
f_gdp1=exp(unlist(gdp1[2]))
e_gdp1=f_gdp1-realgdp_adj_ln[1:5]
f_gdp2=exp(unlist(gdp2[2]))
e_gdp2=f_gdp2-realgdp_adj_ln
#plot the real and forecast
###################################
ts.plot(ts(f_yty1),ts(f_yty2),ts(realgdp[5:14]),gpars=list(col=c("blue","red",'black')))
ts.plot(ts(f_qtq1),ts(f_qtq2),ts(realgdp_adj_qtq),gpars=list(col=c("blue","red",'black')))
ts.plot(ts(f_gdp1),ts(f_gdp2),ts(realgdp_adj_ln),gpars=list(col=c("blue","red",'black')))