非对称加密算法又称公开密钥加密算法，非对称加密是相对于对称加密而言的，对称加密指的是通信双方使用的密钥是一致的，而非对称加密就是算法使用的密钥不一致。

非对称加密的好处是当通信双方没有事先协商密钥的情况下也能进行安全通信，而在互联网普及的今天，很多通信双方往往在事先是无法协商好密钥的，从而非对称加密算法得到了广泛应用，本文主要阐述Diffie-Hellman密钥交换这一非对称加密算法。

传统的加密通信需要通信双方共享一个密钥，即用于加密和解密的密钥，此种方法的一个问题就是双方必须就共享密钥达成一致，但是共享密钥的传输又需要通信，从而该密钥有着被攻击者窃取的风险。在互联网普及的今天，在网络世界中通信各方之间可能从来没有接触过，即需要一种在没有预先共享密钥的情况下能进行安全通信的方法，即所谓的非对称加密算法。

假设A要和B之间需要通信，但是A与B并未共享一个密钥，在此情况下他们之间如何进行安全通信呢？

为了方便阐述非对称加密的概念，假定通信者A与B共享一个公钥，这个公钥是公开的，任何人都可以获得（对于攻击者来说也是如此），该公钥用Kpublic表示。

A可以持有一个私钥KprivateA，A基于这个私钥KprivateA进行某种运算f，即f(KprivateA,Kpublic)。B也随机生成私钥KprivateB进行运算f即f(KprivateB,Kpublic)，紧接着A，B以明文方式交换他们的运算结果（入侵者可以截取到该信息），即此时A获得了f(KprivateB,Kpublic)记为fB，B获得了f(KprivateA,Kpublic) 记为fA。

然后A与B进行运算g，即A运算得到g(fB,KprivateA,Kpublic)，B运算得到g(fA,KprivateB,Kpublic)，分别记做gA和gB，并且存在着这样的运算使得gA=gB，此时gA和gB分别是A与B的新的私钥，即通信中加密/解密的私钥。

从上面的过程来看A，B之间任何一方都无须分发任何敏感的私钥（初始的私钥是各自持有的，无须在信道上传输）。假定在A，B通信的过程中有一个攻击者C截获了他们之间的报文，显然入侵者只能获取Kpublic，f(KprivateB,Kpublic)与f(KprivateA,Kpublic)，而无法获得真正的私钥gA和gB，因此无法解密报文，保证了通信的安全性。下面我们将介绍应用这一过程的算法-Diffie-Hellman密钥交换算法。

Diffie-Hellman密钥交换算法基于数论知识，最初由Whitefield与Martin Hellman在1976年提出，该算法本质上是一个确保共享的私钥穿越不安全网络的方法，它基于单向函数这样一个概念，单向函数的基本思想就是单向函数计算起来相对容易，但求逆运算却非常困难。也就是说，已知x, 我们很容易计算f(x), 但已知f(x), 却很难计算出x。Diffie-Hellman算法运用的单向函数是模运算，如下所示：f(x) = x mod p，已知x与p很容易计算f(x)，但是已知f(x)与p却很难准确计算出x，因为x的取值非常多，特别是当x和p取很大的值时。

为了方便叙述，假设A和B需要进行安全通信，需要安全地生成一个密钥，而中间有一个攻击者C在窃听，其基本步骤如下：

1. A和B公开化达成共识，选择 数a 和 素数p (质数，只能被1和自己整除的数)，假设分别为 a=5 和 p=23 ，可以当成是公钥，这个信息是A，B和攻击者C都掌握的。

2. A随机选择一个数，记为 s1=29 ，即A的私钥，计算单向函数 f(s1) = a**s1 mod p 的值(**表示乘方)，记为f1(此处计算得17)， f1=5**29 mod 23=17 ，然后将计算得到的值发送给B。在这个过程中, B得到单项函数的值17，攻击者C也能截获。

3. B也选择一个数，记为 s2=33 ，即B的私钥, 计算单向函数 f(s2) = a**s2 mod p 的值，记为f2(此处计算得22)， f2=5**33 mod 23=22 ，然后将计算得到的值发送给A。在这个过程中，A得到单向函数的值22，窃听者C也能截获。

4. 定义函数 g1(x)=f2**x mod p ，A计算g1(s1)的值作为密钥，此例中为 g1(29) = 22**29 mod 23=22。

5. 定义函数 g2(x)=f1**x mod p ，B计算g2(s2)的值作为密钥，此例中为 g2(33) = 17**33 mod 23=22 。

上述整个过程如下图1所示：

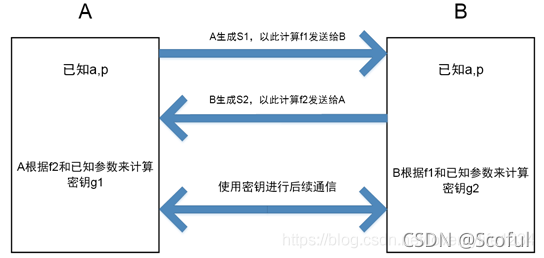
图1 A，B通信过程

可以发现 g1(x)= g2(x) ，即 (a**s2 mod p)**s1 mod p= (a**s1 mod p)**s2 mod p 。事实上根据数论理论可以证明对任意整数，有上式成立。通信双方只需知道公钥a，p以及交换非敏感信息f1，f2就可以完成密钥交换这一工作，从而在后续的通信中使用生成的密钥来加密/解密信息。

使用python进行简单的编程验证，代码如下图2：（运行1000次输出结果为Success）

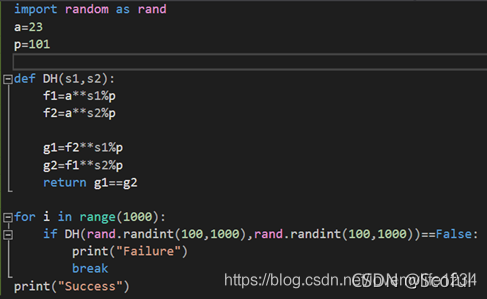
图2 python验证代码

输出结果如下图3：

图3 代码输出结果

Diffie-Hellman算法的有效性依赖于计算离散对数的难度 ,即此时窃听者尽管能截获f1，f2以及获知所用的公钥，但是想从f1、f2、a与p计算出指数s1，s2是十分困难的，进而也就无法计算出私钥g1，g2。

Diffie-Hellman算法让通信双方在完全没有对方任何预先信息的条件下通过不安全信道建立起一个密钥，这个密钥一般作为对称加密的密钥而被双方在后续数据传输中使用。

Diffie-Hellman算法仅当需要时才生成密钥，减小了将密钥存储很长一段时间而致使遭受攻击的机会，除对全局参数即公钥的约定外，密钥交换不需要事先约定其它参数，这也是非对称加密的优势所在。

然而Diffie-Hellman算法也有着以下一些缺点：

1. 通信时没有提供双方身份的任何信息；
2. 该算法是计算密集性的，因此容易遭受阻塞性攻击，即对手请求大量的密钥时本机会花费了相对多的计算资源来求解参数而不是在做真正的工作；
3. 没办法防止重演攻击，即攻击者截获了先前的整个过程的通信报文，然后来重演这一过程，向本机重发一模一样的报文；
4. 容易遭受中间人的攻击，即攻击者C在和A通信时扮演B，在和B通信时扮演A。A和B都与C协商了一个密钥，然后C就可以监听A，B的通信过程；

以上的一些缺点并没有阻止Diffie-Hellman算法在实际工程中的广泛应用，通常可以采用一些辅助技术来弥补上述缺点，如数字签名技术、鉴别协议与MAC（Message Authentication Code）技术等。