洛谷的官方定义：洛谷是一个面向全体学生的信息学竞赛社区，提供了丰富的题库和在线编程环境，旨在帮助学生提高编程能力，增强算法思维，同时也是国内知名的在线评测系统之一。

洛谷是一个 刷题 练习编程网站，收录各色题目，从基础到NOI/CTSC的题目应有尽有。可有些用户初入洛谷时认为它功能繁杂，一时不知该怎么办才好。如果您也遇到了这样的问题，就来看看我为大家整理的洛谷功能全解吧。

注：洛谷写的简略版教程在这，可以先了解个大概。

第一章 进入方式

这有什么好看的？不就是注册和登陆吗...... 其实，洛谷的注册登陆的细节也是值得细细研究的！

1.1 基础操作

初入洛谷，在右上角可以发现图中内容。有账号的话点登录，没有就点注册。 好像没啥好研究的

1.2 两步验证

终于登陆成功了！但你以为到这就结束了吗.......不！为了保证账号安全，最好使用两步验证。两步验证设置后，登陆时将会向您索要一个每分钟变化的动态密码。

进入方式：鼠标移至右上角头像->个人设置->安全设置->滚到页面最底下->设置两步验证

看上面的图。对于两步验证的过程，洛谷已经解释得很清楚了，此处不再赘述。

1.3 安全邮箱和安全手机

现在总该结束了吧？还没有！为了保证安全，建议绑定安全邮箱和安全手机。（如果没有电子邮箱、手机，也可以不绑定） 这个绑定应该谁都会的吧......

第二章 侧栏与主界面介绍

主界面就不用多说了吧......

洛谷左侧有一个侧栏，有许多按钮，将一一简单介绍。

2.1 蓝底白色洛谷标志

点击它，可以回到洛谷首页。

2.2 “应用>>”

点击它，会跳出6个应用。主题商店可以让你更改洛谷的主题颜色；图片上传让您上传完图片之后就可以复制网址，在洛谷站内用超链接；在线IDE可让你在线输入代码进行测试，再也无须自己搭建编程环境了；云剪贴板可以让您记录个人笔记，或复制文字资料/代码并生成短链接分享；咕值排名是洛谷对用户活跃程度评分后得出的排名；反馈问题则是让您进入讨论区中的反馈、申请、工单专版（关于讨论区是什么，请跳至2.7）。

2.3 题库

让您跳至洛谷题库。详情请看第四章。

2.4 题单

让您跳至洛谷题单。详情请看第四章。

2.5 比赛

让您跳至比赛界面。详情请看第四章。

2.6 记录

让您跳至提交题目的记录界面。详情请看第四章。

2.7 讨论

讨论可从主页（往下拉）或侧栏进入。

在此处有站务版、题目总版、学术版、灌水区与反馈、申请、工单专版，共5个板块。这些板块的名字很好理解，此处不再解释。您可以阅读帖子，或者选择一个板块发布帖子。

2.8 打卡

打卡在主页即可直接看到。

如图，打卡很“玄学”， 都是与“运势”有关的。但打卡连续天数规则有些复杂：设你的打卡间断 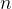天，原先连续打卡了 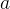天，则现在的连续打卡天数为 天。

洛谷还专门做了道题说明这个规则，详见洛谷的 P1664 每日打卡心情好 这道题。

2.9 跳题及其右侧栏目

如图，跳题功能就在打卡的左下角。有两种形式：一是输入题号后跳转至对应题目，二是随机跳转至任一题目。右侧是您通过题数的月统计图和统计图（关于什么是通过题目，请看我的 另一篇文章 ）。

2.10 犇犇

把主页拉到最下方（如图所示），写好内容后 开炮 发射犇犇，内容会进入您的个人中心。

第三章 个人中心

如图所示，当您把鼠标悬停在右上角头像，可看到一个小窗口。

3.1 直接点击头像或用户名

如图，会进入“标准个人页面”。有主页、动态、练习等栏目。主页中，可填写个人介绍，以及查看自己的一些数据（作者尚未摸清“咕值”的作用）。点击“个人设置”后进入的页面将在3.2中介绍。点击“个人博客”后进入的页面将在3.6中介绍。“动态”即您发布的每一条犇犇。

3.2 个人设置

点进去后，如图，会进入“安全设置界面”。在3.1中，点击“个人设置”也可进入此界面。

头像设置就不用说了吧...... RemoteJudge与OpenID洛谷已经解释得很清楚了，此处不再赘述。关于Retome Judge的着重介绍在4.2中。这里重点说说奖项认证和CCF等级认证。假如您在某场编程比赛中获奖了，那么在一般情况下，洛谷会将其自动进行认证，并转化为CCF等级。但洛谷也有可能出现漏认证的情况，这时您就需要按洛谷的指引，自行手动认证。CCF等级可以设为显示或隐藏，以带底色的白勾展示。

CCF等级规则如下：

1. 一级：NOIP初赛（CSP-J/S第一轮）60分以上（此级不颁发等级证书）；
2. 二级：NOIP初赛（CSP-J/S第一轮）80分以上（此级不颁发等级证书）；
3. 三级：进入NOIP复赛（CSP-J/S第二轮）；
4. 四级：在NOIP普及组（或提高组）复赛（CSP-J/S第二轮）中成绩列全国前50%；
5. 五级：在NOIP普及组复赛（CSP-J第二轮）中成绩列全国前20%；
6. 六级：在NOIP提高组复赛（CSP-S第二轮）中成绩列全国前20%；
7. 七级：在NOIP提高组复赛（CSP-S第二轮）中成绩列全国前10%；
8. 八级：NOI铜牌或累计积分250分以上的选手可获得八级资格。
9. 九级：NOI银牌或累计积分500分以上的选手可获得九级资格。
10. 十级：NOI金牌或累计积分1000分以上的选手可获得十级资格。

积分折算规则不详细说明，有兴趣的读者朋友们可以查看 这个链接 。

“使用偏好”里我的台词已经被洛谷抢了......

“安全设置”里可以更改用户名（注意，一年只能改一次，请谨慎修改）、改密码、绑定/解绑安全邮箱和安全手机，还可根据洛谷的指引取消两步验证。

3.3 我的收藏

如图，会进入“标准个人页面”的收藏区，展示您收藏的题单、题目等。

3.4 我的团队

如图，会进入“标准个人页面”的“我的”栏目中“我加入的团队”小栏目，展示您加入的团队，也可自己创建一个团队。

3.5 我的比赛

会进入“我参加的比赛”小栏目，展示您参加过的比赛。

3.6 我的博客

在“标准个人页面”中点击“个人博客”同样可以进入该界面。会进入您的个人博客，若您没有博客，则需要创建一个。

如图，这是个人博客的首页。点击左上角的图标后，还可以管理后台，用于写文章和进行一些设置。

3.7 我的题库

会进入“题库”页中“我创建的题目”栏目。可自行创建题目或编辑题目，但不会展示在公共题库。

3.8 锁定&登出

如图，点击“锁定”后，会直接把账户锁住，需要解锁，且无法进行任何操作。

点击“登出”后，会让您重新登录。登出不会导致账户解锁。

第四章 开肝！！！

呼，终于把前面的东西讲完了......

这一章主要介绍洛谷的题目。

4.1 开始做题

可以从侧栏的“题库”按钮中进入做题。

如图，这是点进去后展示的前 12 13题。状态中，√表示已通过（AC了！），×表示未通过（反正做了，但没AC），--表示没坐过这题。比如在图中，我做对了题号为P1000的题和P1001的题，做错了题号为P1009的题，其他题没做。

题目的标签描述了这题的特征。有年份标签（用蓝色表示），比如P1002的年份标签是2002，表示该题是在2002年被发布的；有竞赛标签（用浅蓝色表示），比如P1002的竞赛标签是“NOIp普及组”，表示其出自NOIp普及组；有算法标签，用于标明该题所使用的算法。您可以设置是否显示算法标签。

每题都有对应的难度。入门最简单，NOI/NOI+/CTSC最难。

（2022.1）

（2023.8）

在如图所示的位置，可以筛选难度和标签，还可以搜索题目。在本文初版（2022.1）时，主题库共7066道题；现在（2023.8），主题库已经有了8347道题。（一年半更新1000多道题，效率很高！！！）

提交代码的方法是：点击题目标题（蓝色字）进入题目后，点击“提交答案”，选择编程语言后可直接编写代码（会自动缩进、补齐右括号等）。比如，您在 主题库的P1001 （A+B Problem） 这道著名的试机题 这道题中编写了如下C++11代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int a,b;
    cin>>a>>b;
    cout<<a+b;
    return 0;
再点击“提交评测”后，就可以上传代码。 
 
4.2 特殊介绍-Retome Judge
 
在3.2中，也提到过Retome Judge。但当时只是一笔带过，这里正好需要再一次介绍，我就来具体讲一讲。
 
如图，Retome Judge的原理是：在洛谷中提交完代码，代码会被发送至另一个在线判题系统进行评测。评测完后，洛谷会抓取该网站的评测结果，再显示出来。若未绑定账户，则会使用公用账户进行评测；否则，会使用您的个人账户进行评测，您在该网站的评测记录也会相应地增加一条。
 
在洛谷，RetomeJudge有：CodeForces、ATCoder、SPOJ、UVA。其中，UVA在境内的可访问性较差需要V*N；ATCoder无法绑定账号，其余均可绑定（关于绑定账号的介绍，请看3.2中的图片）。
 
入门与面试其实也是洛谷自己的题库，不属于Retome Judge。
 
4.3 题目的题解、提交记录、讨论区、推荐题目
 
如图，在每道题中（以主题库中的P1001 A+B Problem为例），都会有提交纪录、查看题解（用户自编题目除外）、相关讨论、推荐题目。 
 
 提交纪录，如图，展示了用户提交该题的纪录（表格形式）：
 
可看到他们的提交状态、分数、语言、用时与内存占用，还可以对记录进行筛选。您可点击用户状态来查看他们各测试点的详细状态。若您的分数达到一定值，您还可能看到他的源代码。点击题目编号或标题（即图中的“P1001 A+B Problem”）可以回到原题。
 
题解，如图，展示了用户提交的题目解析：
 
相关讨论展示了用户关于此题的讨论（根据洛谷的规定，千万不要在这里发题解！！！）；推荐题目展示了在刷做完后，洛谷建议您继续做的题目。
 
 4.4 题单
 
由一些题目组成的集合叫做题单。题单主要分为两种：优秀用户题单和官方题单。如图所示：
 
 您可以查看题单的题目列表以及您的完成进度。
 
4.5 比赛
 
和许多其他大型OJ一样，洛谷会举办比赛，有官方的，也有非官方的。带有官方绿底白色Rated标记的比赛及官方比赛，会影响咕值；非官方比赛则不会。您还可在比赛界面查看比赛状态，或进入做题。
 
上图是我写作时的比赛列表。最上面和最下面的比赛都没有Rated标记，其余比赛都有。其中，除了最下方的比赛结束了以外，其余都未开始。
 
 如图是一个未开始比赛的报名界面。报名比赛且比赛开始后，您就可以做题了，还可以查看得分情况排行榜。
 
如图，还可查看一场未开始的比赛距离开始时间的时长。
 
就算比赛已经结束了，您也能查看提交排行榜与题目列表，并点进去做题。您也会被记入排行榜中。 
 
4.6 纪录
 
如图，在该界面可以看到自己的所有做题纪录，格式与每题的做题纪录相同。
 
终于可以把“未更完”删掉了......本文到此就结束了。若想了解更多有关洛谷的内容，以后我还会更新更多关于洛谷的文章，并放入专栏“洛谷入门系列”内。
                                    请注意，洛谷个人用户可加入的团队是有上限的，超出了则会被限制加入其他团队。云剪贴板可以存放任何文本，保存后的文本，通过点击 “查看”，将文本的网页链接分享给其他人。在左侧点击 “讨论” 进入讨论区域，选择相应的板块进行发帖，具体规则查看。通过 “个人中心—我的”，创建团队，普通用户可以创建 3 个团队。通过 “头像—开通博客”，输入符合要求的博客个性地址，即可开通博客。之后请在个人博客页面寻找对应按钮进入 “管理后台” 管理你的文章。将完成的代码输入在文本框中，点击 “提交评测”。调出 “在线 IDE”；
                                    洛谷创建于2013年6月15日，至今已有数万用户，致力于为OIers/ACMers提供清爽、快捷的编程体验。它不仅仅是一个在线测题系统，更拥有强大的社区、在线学习功能。同时，许多教程内容都是由五湖四海的ers提供的，保证了内容的广泛性。无论是初学oi的蒟蒻，还是久经沙场的神犇，均可从洛谷Online Judge获益，也可以帮助他人，共同进步。
洛谷评测系统搭建与Linux上，采用分布式集群保...
                                    洛谷更多题库详见我的另一个博客 ：
https://www.cnblogs.com/hsjj/p/P1553.html
有问题欢迎邮件至hpzhangjunjiell@163.com
CSDN用来写技术交流
博客园用来写代码和题库~
                                    思路1（洛谷题解）
设n维球体为α，其半径为r（注意，这是一个设而不求。），其球心X的坐标为(x_1,x_2,…,x_n )。∀A_1,A_2,…,A_(n+1)∈α，点A_i (1≤i≤n+1)坐标为(a_((i,1) ),a_((i,2) ),…,a_((i,n) ) )。由n维球体的定义，得方程组：
{█((a_((1,1) )-x_1 )^2+(a_((1,2) )-x_2 )^2+⋯+(a_((1,n) )-x_n )^2=r^2@(a_((2,1) )-x_1 )^2+(a_((2,2) )-x_2 )^2+⋯+(a_((2,n) )-x_n )^2=r^2@⋮@(a_((n+1,1) )-x_1 )^2+(a_((n+1,2) )-x_2 )^2+⋯+(a_((n+1,n) )-x_n )^2=r^2 )┤.
从上往下，将第1个方程与第2个方程相减，将第2个方程与第3个方程相减，……，将第n个方程与第(n+1)个方程相减，得：
{█(∑_(i=1)^n▒2(a_((1,i) )-a_((2,i) ) )  x_i=∑_(i=1)^n▒(a_((1,i) )+a_((2,i) ) )(a_((1,i) )-a_((2,i) ) ) @∑_(i=1)^n▒2(a_((2,i) )-a_((3,i) ) )  x_i=∑_(i=1)^n▒(a_((2,i) )+a_((3,i) ) )(a_((2,i) )-a_((3,i) ) ) @⋮@∑_(i=1)^n▒2(a_((n,i) )-a_((n+1,i) ) )  x_i=∑_(i=1)^n▒(a_((n,i) )+a_((n+1,i) ) )(a_((n,i) )-a_((n,i) ) ) )┤.
这是一个线性方程组，其增广矩阵为[■(2(a_((1,1) )-a_((2,1) ) )&⋯&2(a_((1,n) )-a_((2,n) ) )&∑_(i=1)^n▒(a_((1,i) )+a_((2,i) ) )(a_((1,i) )-a_((2,i) ) ) @⋮&⋱&⋮&⋮@2(a_((n,1) )-a_((n+1,1) ) )&⋯&2(a_((n,n) )-a_((n+1,n) ) )&∑_(i=1)^n▒(a_((n,i) )+a_((n+1,i) ) )(a_((n,i) )-a_((n+1,i) ) ) )]，可用列主元高斯消元法求得其解。
n(n∈N_+ )维空间中到两个互不重合的点的距离相等的点的集合叫做这两个点的垂直平分图形。
求n维空间中两点的垂直平分图形的方程的基本思路：
设点A坐标为(a_1,a_2,…,a_n ),点B的坐标为(b_1,b_2,…,b_n )，A≠B，它们的垂直平分图形为β。取∀X∈β，其坐标为(x_1,x_2,…,x_n )。
由垂直平分图形的意义，得：
|AX|=|BX|⇔|AX|^2=|BX|^2⇔∑_(i=1)^n▒(a_i-x_i )^2 =∑_(i=1)^n▒(b_i-x_i )^2 ⇔(∑_(i=1)^n▒〖a_i〗^2 )-2(∑_(i=1)^n▒〖a_i x_i 〗)+(∑_(i=1)^n▒〖x_i〗^2 )=(∑_(i=1)^n▒〖b_i〗^2 )-2(∑_(i=1)^n▒〖b_i x_i 〗)+(∑_(i=1)^n▒〖x_i〗^2 )⇔∑_(i=1)^n▒〖2(a_i-b_i ) x_i 〗=∑_(i=1)^n▒(a_i+b_i )(a_i-b_i ) .
最后出来的这个等式就是垂直平分图形的方程。
回到题目中，对于∀A_1,A_2,…,A_(n+1)∈α，取A_1,A_2为一对，A_2,A_3为一对，……，A_n,A_(n+1)为一对代入垂直平分图形的方程中，惊奇地发现得到的线性方程组与思路1中相同，接下来的解法也相同。