卡尔曼滤波和粒子滤波的理论介绍

李为

围观者

这里先总体介绍下，原文转自：

http://www. cnblogs.com/gaoxiang12/ p/5560360.html

任何传感器，激光也好，视觉也好，整个SLAM系统也好，要解决的问题只有一个： 如何通过数据来估计自身状态。 每种传感器的测量模型不一样，它们的精度也不一样。换句话说，状态估计问题，也就是“ 如何最好地使用传感器数据 ”。可以说，SLAM是状态估计的一个特例。

1. 离散时间系统的状态估计

记机器人在各时刻的状态为 x_1,\cdots,x_k ，其中k是离散时间下标。在SLAM中，我们通常要估计机器人的位置，那么系统的状态就指的是机器人的位姿。用两个方程来描述状态估计问题：

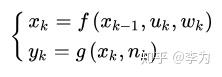
解释一下变量：

f-运动方程

u- 输入

w- 输入噪声

g- 观测方程

y- 观测数据

n- 观测噪声

运动方程描述了状态 x_{k-1} 是怎么变到 x_k 的，而观测方程描述的是从 x_k 是怎么得到观察数据 y_k 的。

请注意这是一种抽象的写法。当你有实际的机器人，实际的传感器时，方程的形式就会变得具体，也就是所谓的 参数化 。例如，当我们关心机器人空间位置时，可以取 x_k=[x,y,z]_k 。进而，机器人携带了里程计，能够得到两个时间间隔中的相对运动，像这样 \Delta x_k=[\Delta x, \Delta y, \Delta z]_k ，那么运动方程就变为：

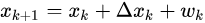
同理，观测方程也随传感器的具体信息而变。例如激光传感器可以得到空间点离机器人的距离和角度，记为 y_k=[r,\theta]_k ，那么观测方程为：

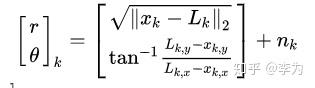
其中 L_k=[L_{k,x},L_{k,y}] 是一个2D路标点。

举这几个例子是为了说明， 运动方程和观测方程具体形式是会变化的 。但是，我们想讨论更一般的问题：当我不限制传感器的具体形式时，能否设计一种方式，从已知的u,y（输入和观测数据）从，估计出x呢？

这就是最一般的状态估计问题。我们会根据f,g是否线性，把它们分为 线性/非线性系统 。同时，对于噪声w,n，根据它们是否为高斯分布，分为 高斯/非高斯噪声 系统。最一般的，也是最困难的问题，是非线性-非高斯(NLNG, Nonlinear-Non Gaussian)的状态估计。下面先说最简单的情况：线性高斯系统。

2. 线性高斯系统(LG，Linear Gaussian)

在线性高斯系统中，运动方程、观测方程是线性的，且两个噪声项服从零均值的高斯分布。这是最简单的情况。简单在哪里呢？主要是因为 高斯分布经过线性变换之后仍为高斯分布 。而对于一个高斯分布，只要计算出它的一阶和二阶矩，就可以描述它（高斯分布只有两个参数 \mu,\Sigma ）。

线性系统形式如下：

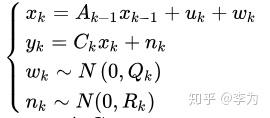
其中 Q_k,R_k 是两个噪声项的协方差矩阵。 A,C 为转移矩阵和观测矩阵。

对LG系统，可以用贝叶斯法则，计算x的后验概率分布——这条路直接通向 卡尔曼滤波器 。卡尔曼是线性系统的递推形式（recursive，也就是从 x_{k-1} 估计 x_k ）的无偏最优估计。由于解释EKF和UKF都得用它，所以我们来推一推。如果读者不感兴趣，可以跳过公式推导环节。

符号：用 \hat{x} 表示 x 的后验概率，用 \tilde{x} 表示它的先验概率。因为系统是线性的，噪声是高斯的，所以状态也服从高斯分布，需要计算它的均值和协方差矩阵。记第k时刻的状态服从：

我们希望得到状态变量 x 的最大后验估计（MAP，Maximize a Posterior），于是计算：

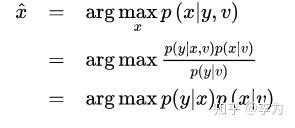
第二行是贝叶斯法则，第三行分母和 x 无关所以去掉。

第一项即观测方程，有：

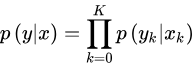
很简单。

第二项即运动方程

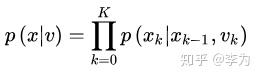
也很简单。

现在的问题是如何求解这个最大化问题。对于高斯分布，最大化问题可以变成最小化它的负对数。当我对一个高斯分布取负对数时，它的指数项变成了一个二次项，而前面的因子则变为一个无关的常数项，可以略掉（这部分我不敲了，有疑问的同学可以问）。于是，定义以下形式的最小化函数：

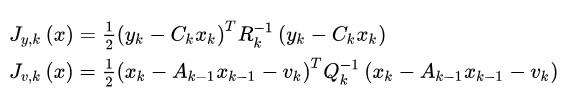
那么最大后验估计就等价于：

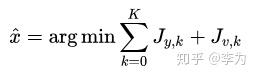
这个问题现在是二次项和的形式，写成矩阵形式会更加清晰。定义：

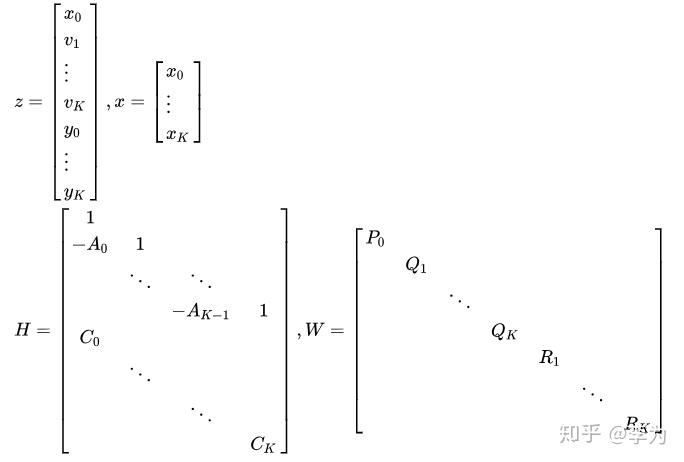
就得到矩阵形式的，类似最小二乘的问题：

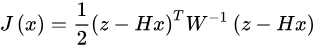
于是令它的导数为零，得到：

(*)

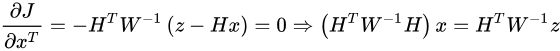
读者会问，这个问题和卡尔曼滤波有什么问题呢？事实上， 卡尔曼滤波就是递推地求解(*)式的过程 。所谓递推，就是只用 x_{k-1} 来计算 x 。对(*)进行Cholesky分解，就可以推出卡尔曼滤波器。详细过程限于篇幅就不推了，把卡尔曼的结论写一下：

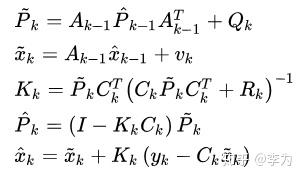
前两个是预测，第三个是卡尔曼增益，四五是校正。

另一方面，能否直接求解(*)式，得到 \hat{x} 呢？答案是可以的，而且这就是优化方法（batch optimization）的思路：将所有的状态放在一个向量里，进行求解。与卡尔曼滤波不同的是，在估计前面时刻的状态（如 x_1 ）时，会用到后面时刻的信息（ y_2,y_3 等）。从这点来说，优化方法和卡尔曼处理信息的方式是相当不同的。

增加一篇KF的说明：

http:// blog.csdn.net/baimafuji nji/article/details/50646814

一、引言

下面我们引用文献【1】中的一段话作为本文的开始：

想象你在黄昏时分看着一只小鸟飞行穿过浓密的丛林，你只能隐隐约约、断断续续地瞥见小鸟运动的闪现。你试图努力地猜测小鸟在哪里以及下一时刻它会出现在哪里，才不至于失去它的行踪。或者再想象你是二战中的一名雷达操作员，正在跟踪一个微弱的游移目标，这个目标每隔10秒钟在屏幕上闪烁一次。或者回到更远的从前，想象你是开普勒，正试图根据一组通过不规则和不准确的测量间隔得到的非常不精确的角度观测值来重新构造行星的运动轨迹。在所有这些情况下，你都试图根据随对问变化并且带有噪声的观察数据去估计物理系统的状态（例如位置、速度等等）。这个问题可以被形式化表示为时序概率模型上的推理，模型中的转移模型描述了运动的物理本质，而传感器模型则描述了测量过程。为解决这类问题，人们发展出来了一种特殊的表示方法和推理算法——卡尔曼滤波。

二、基本概念

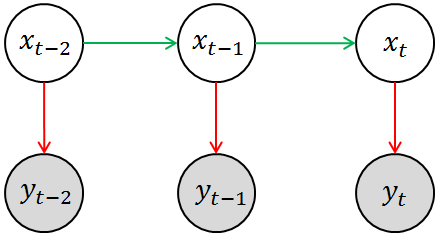
回想一下HMM的基本模型（如下图所示），其中涂有阴影的圆圈（ y t-2, y t-1, y t）相当于是观测变量，空白圆圈（ x t-2, x t-1, x t）相当于是隐变量。这其实揭示了卡尔曼滤波与HMM之间拥有很深的渊源。回到刚刚提及的那几个例子，你所观测到的物体状态（例如雷达中目标的位置或者速度）相当于是对其真实状态的一种估计（因为观测的过程中必然存在噪声），用数学语言来表述就是 P ( y t | x t)，这就是模型中的测量模型或测量概率（Measurement Probability）。另外一方面，物体当前的（真实）状态应该与其上一个观测状态相关，即存在这样的一个分布 P ( x t | x t-1)，这就是模型中的转移模型或转移概率（Transition Probability）。当然，HMM中隐变量必须都是离散的，观测变量并无特殊要求。

而从信号处理的角度来讲，滤波是从混合在一起的诸多信号中提取出所需信号的过程 [2]。例如，我们有一组含有噪声的行星运行轨迹，我们希望滤除其中的噪声，估计行星的真实运动轨迹，这一过程就是滤波。如果从机器学习和数据挖掘的角度来说，滤波是一个理性智能体为了把握当前状态以便进行理性决策所采取的行动 [1]。比如，前两天我们没出门，但是我们可以从房间里观察路上的行人有没有打伞（观测状态）来估计前两天有没有下雨（真实状态）。基于这些情况，现在我们要来决策今天（是否会有雨以及）外出是否需要打伞，这个过程就是滤波。读者应该注意把握上面两个定义的统一性。

所谓估计就是根据测量得出的与状态X(t) 有关的数据Y(t) = h [X(t)] + V(t) 解算出X(t)的计算值 \hat{X}(t) ，其中随机向量V(t) 为测量误差， \hat{X} 称为X的估计，Y 称为 X 的测量。因为 \hat{X}(t)

是根据Y(t) 确定的．所以 \hat{X}(t) 是Y(t) 的函数。 \hat{X} 是Y 的线性函数，则 \hat{X} 称作 X 的线性估计。设在 [ t 0, t 1] 时间段内的测量为Y，相应的估计为 \hat{X}(t) ，则

当 t = t 1 时， \hat{X}(t) 称为X(t)的估计；
当 t > t 1 肘， \hat{X}(t) 称为X(t)的预测；
当 t < t 1 时， \hat{X}(t) 称为X(t)的平滑。

最优估计是指某一指标函数达到最值时的估计。卡尔曼滤波就是一种线性最优滤波器。

因为后面会用到，这里我们补充一下关于协方差矩阵的概念。

设 n 维随机变量（ X 1, X 2, …, X n）的2阶混合中心距

σ ij= cov( X i, X j) = E[( X i-E( X i))( X j-E( X j))], (i,j = 1, 2, …, n)

都存在，则称矩阵

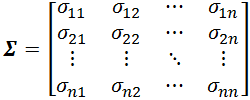
为 n 维随机变量（ X 1, X 2, …, X n）的协方差矩阵，协方差矩阵是一个对称矩阵，而且对角线是各个维度的方差。

维基百科中还给出了协方差矩阵的一些重要性质，例如下面这两条（此处不做具体证明）。后续的内容会用到其中的第一条。

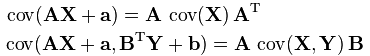
三、卡尔曼滤波的方程推导

直接从数学公式和概念入手来考虑卡尔曼滤波无疑是一件非常枯燥的事情。为了便于理解，我们仍然从一个现实中的实例开始下面的介绍，这一过程中你所需的预备知识仅仅是高中程度的物理学内容。

假如现在有一辆在路上做直线运动的小车（如下所示），该小车在 t 时刻的状态可以用一个向量来表示，其中 p t 表示他当前的位置， v t表示该车当前的速度。当然，司机还可以踩油门或者刹车来给车一个加速度 u t， u t相当于是一个对车的控制量。显然，如果司机既没有踩油门也没有踩刹车，那么 u t就等于0。此时车就会做匀速直线运动。

如果我们已知上一时刻 t -1时小车的状态，现在来考虑当前时刻 t 小车的状态。显然有

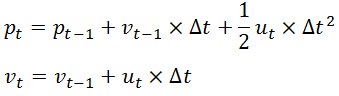
易知，上述两个公式中，输出变量都是输入变量的线性组合，这也就是称卡尔曼滤波器为线性滤波器的原因所在。既然上述公式表征了一种线性关系，那么我们就可以用一个矩阵来表示它，则有

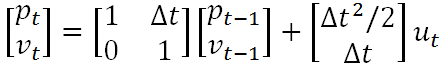
如果另其中的

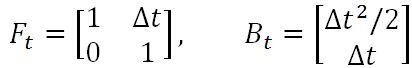
则得到卡尔曼滤波方程组中的第一条公式——状态预测公式，而 F 就是状态转移矩阵，它表示我们如何从上一状态来推测当前状态。而 B 则是控制矩阵，它表示控制量 u 如何作用于当前状态。

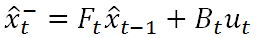
（1）

上式中 x 顶上的hat表示为估计值（而非真实值）。等式左端部分的右上标“-”表示该状态是根据上一状态推测而来的，稍后我们还将对其进行修正以得到最优估计，彼时才可以将“-”去掉。

既然我们是在对真实值进行估计，那么就理应考虑到噪声的影响。实践中，我们通常都是假设噪声服从一个0均值的高斯分布，即 Noise~Guassian (0, σ )。例如对于一个一维的数据进行估计时，若要引入噪声的影响，其实只要考虑其中的方差 σ 即可。当我们将维度提高之后，为了综合考虑各个维度偏离其均值的程度，就需要引入协方差矩阵。

回到我们的例子，系统中每一个时刻的不确定性都是通过协方差矩阵 Σ 来给出的。而且这种不确定性在每个时刻间还会进行传递。也就是说不仅当前物体的状态（例如位置或者速度）是会（在每个时刻间）进行传递的，而且物体状态的不确定性也是会（在每个时刻间）进行传递的。这种不确定性的传递就可以用状态转移矩阵来表示，即（注意，这里用到了前面给出的关于协方差矩阵的性质）

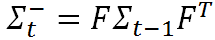
但是我们还应该考虑到，预测模型本身也并不绝对准确的，所以我们要引入一个协方差矩阵 Q 来表示预测模型本身的噪声（也即是噪声在传递过程中的不确定性），则有

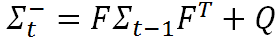
（2）

这就是卡尔曼滤波方程组中的第二条公式，它表示不确定性在各个时刻间的传递关系。

继续我们的小汽车例子。你应该注意到，前面我们所讨论的内容都是围绕小汽车的真实状态展开的。而真实状态我们其实是无法得知的，我们只能通过观测值来对真实值进行估计。所以现在我们在路上布设了一个装置来测定小汽车的位置，观测到的值记为V(t)。而且从小汽车的真实状态到其观测状态还有一个变换关系，这个变换关系我们记为 h (•)，而且这个 h (•)还是一个线性函数。此时便有（该式前面曾经给出过）

Y(t) = h [X(t)] + V(t)

其中V(t)表示观测的误差。既然 h (•)还是一个线性函数，所以我们同样可以把上式改写成矩阵的形式，则有

Yt= H xt + v

就本例而言，观测矩阵 H = [1 0]，这其实告诉我们 x 和 Z 的维度不一定非得相同。在我们的例子中， x 是一个二维的列向量，而Z只是一个标量。此时当把 x 与上面给出的 H 相乘就会得出一个标量，此时得到的 Y 就是 x 中的首个元素，也就是小车的位置。同样，我们还需要用一个协方差矩阵R来取代上述式子中的 v 来表示观测中的不确定性。当然，由于 Z 是一个一维的值，所以此时协方差矩阵R也只有一维，也就是只有一个值，即观测噪声之高斯分布的参数 σ 。如果我们有很多装置来测量小汽车的不同状态，那么Z就会是一个包含所有观测值的向量。

接下来要做的事情就是对前面得出的状态估计进行修正，具体而言就是利用下面这个式子

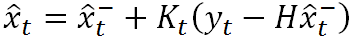
（4）

直观上来说，上式并不难理解。前面我们提到， \hat{x}^-_t 是根据上一状态推测而来的，那么它与“最优”估计值之间的差距现在就是等式右端加号右侧的部分。 y_t-H\hat{x}^-_t 表示实际观察值与预估的观测值之间的残差。这个残差再乘以一个系数 K 就可以用来对估计值进行修正。 K 称为卡尔曼系数，它也是一个矩阵，它是对残差的加权矩阵，有的资料上称其为滤波增益阵。

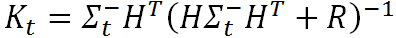
（3）

上式的推导比较复杂，有兴趣深入研究的读者可以参阅文献【2】（P35~P37）。如果有时间我会在后面再做详细推导。但是现在我们仍然可以定性地对这个系数进行解读：滤波增益阵首先权衡预测状态协方差矩阵 Σ 和观测值矩阵R的大小，并以此来觉得我们是更倾向于相信预测模型还是详细观测模型。如果相信预测模型多一点，那么这个残差的权重就会小一点。反之亦然，如果相信观察模型多一点，这个残差的权重就会大一点。不仅如此，滤波增益阵还负责把残差的表现形式从观测域转换到了状态域。例如本题中观测值 Z 仅仅是一个一维的向量，状态 x 是一个二维的向量。所以在实际应用中，观测值与状态值所采用的描述特征或者单位都有可能不同，显然直接用观测值的残差去更新状态值是不合理的。而利用卡尔曼系数，我们就可以完成这种转换。例如，在小车运动这个例子中，我们只观察到了汽车的位置，但K里面已经包含了协方差矩阵 P 的信息（ P 里面就给出了速度和位置的相关性），所以它利用速度和位置这两个维度的相关性，从位置的残差中推算出了速度的残差。从而让我们可以对状态值 x 的两个维度同时进行修正。

最后，还需对最优估计值的噪声分布进行更新。所使用的公式为

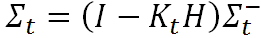
（5）

至此，我们便获得了实现卡尔曼滤波所需的全部五个公式，我在前面分别用（1）~（5）的标记进行了编号。我现在把它们再次罗列出来：

我们将这五个公式分成预测组和更新组。预测组总是根据前一个状态来估计当前状态。更新组则根据观测信息来对预测信息进行修正，以期达到最优估计之目的。

四、一个简单的实例

当然，你可能困惑于卡尔曼滤波是否真的有效。下面利用文献[4]中给出的例子（为提升显示效果，笔者略有修改）来演示卡尔曼滤波的威力。这个例子模拟质点进行匀速直线运动（速度为1），然后引入一个非常大的噪声，再用卡尔曼滤波来对质点的运动状态进行轨迹。注意是匀速直线运动，所以其中不含有控制变量。

Z=(1:100); %观测值  
noise=randn(1,100); %方差为1的高斯噪声  
Z=Z+noise;  
X=[0; 0]; %状态  
Sigma = [1 0; 0 1]; %状态协方差矩阵  
F=[1 1; 0 1]; %状态转移矩阵  
Q=[0.0001, 0; 0 0.0001]; %状态转移协方差矩阵  
H=[1 0]; %观测矩阵  
R=1; %观测噪声方差  
figure;  
hold on;  
for i=1:100  
  X_ = F*X;  
  Sigma_ = F*Sigma*F'+Q;  
  K = Sigma_*H'/(H*Sigma_*H'+R);  
  X = X_+K*(Z(i)-H*X_);