ICLR 2022有哪些值得关注的投稿？

这篇文章有幸得到6-6-8-10的评分，最后入选ICLR的spotlight，这里来厚颜无耻地来推销一下自己的文章~

这篇文章通过度量神经网络权重里的信息量，从而得以对网络的泛化能力进行衡量。我们希望这个信息度量能够帮助提高深度学习的解释性，并且在未来能够用于设计增强网络训练的算法。

• 论文地址：

我们知道，解释神经网络的泛化能力是近年来人工智能领域的一项热点研究。而神经网络中储存的信息量被认为是可以衡量网络泛化能力的指标。如果我们能计算神经网络中的信息量，则可以解释和推断网络的泛化能力，解开深度学习的黑箱，并且指导其优化和设计。

在这篇文章中，我们提出了一种能快速计算神经网络权重中储存数据信息量的算法，并且基于此构建了一种新的信息瓶颈(PAC-Bayes IB)。我们在实验中证明，这种信息度量能从多个角度解释和追踪网络的泛化能力，比如在不同的宽度和深度，数据大小，数据噪音程度，批次大小等。并且，使用该种信息量作为约束能够训练更好的神经网络。

背景：信息瓶颈和信息论深度学习

我们知道Tishby老爷子在2000年就提出了一个叫信息瓶颈 (Information Bottleneck, IB) ^[1] 的东西。顺便提一句老爷子在21年8月逝世，信息瓶颈也可以说是老爷子一辈子的代表作了，后来由其团队在2015年 ^[2] 提出信息瓶颈是一种可以解释神经网络的工具，被Hinton高度赞扬：

信息瓶颈极其有趣，我要再听一万遍才能真正理解它，当今能听到如此原创的想法非常难得，或许它就是解开谜题的那把钥匙。——Geoffrey Hinton

关于信息瓶颈的介绍知乎上已经珠玉在前 ^[3] ，这里就不再赘述了，简单介绍一下：

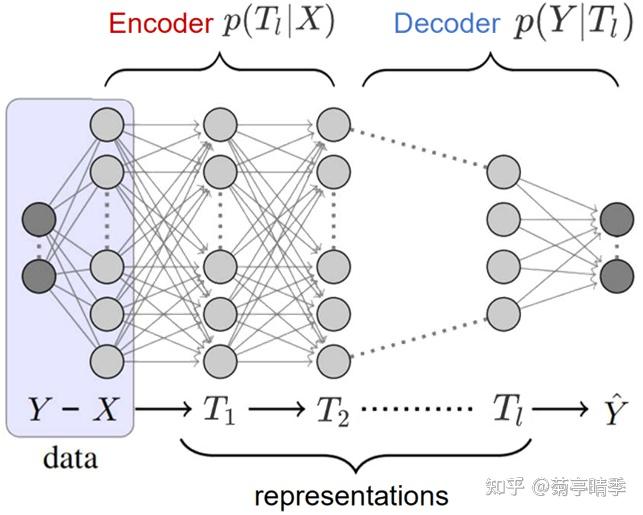
如上图，我们可以把一个全连接网络的任意一层切开得到其中间特征 T_l ，那么我们可以用 p(T_l|X) 和 p(\hat{Y}|T_l) 分别代表编码器和解码器。同时，我们也可以尝试度量特征里所包含的关于输入 X 和样本标签 Y 的信息量，写成一个基于表征的信息瓶颈：

\min I(T;X)-\beta I(T;Y)

这里的 I 是互信息。那么，Tishby团队发现神经网络的训练过程遵循着 " 记忆-遗忘" 两阶段的的过程。在记忆阶段，神经网络尝试记住所有的标签信息，即不断提高 I(T;Y) ；在遗忘阶段，神经网络尝试在保持标签信息的同时，遗忘掉关于输入的信息，即降低 I(T;X) 。呈现出来的结果就是下图中，Y轴是标签信息，X轴是输入信息，每一条线是网络中的一层。可以看到，标签信息随着训练一直在提高，对应了记忆阶段；而输入信息基本是先升高，再下降，对应了遗忘阶段。

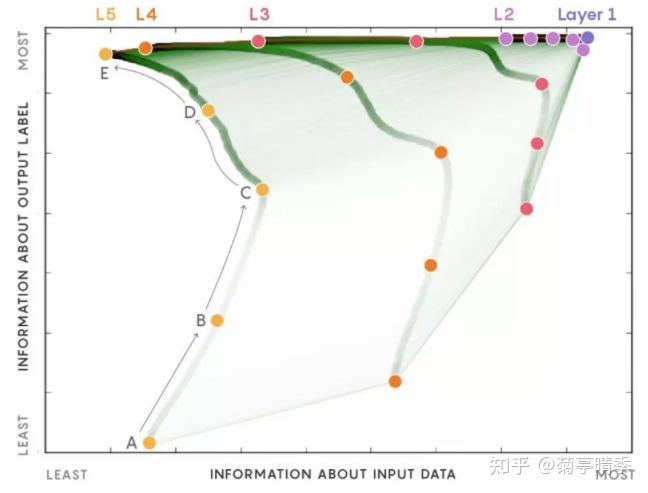
这个发现很有趣。因为如果我们知道网络是"通过遗忘来学习"，我们就可以专门设计目标函数来加强网络的训练，比如后续的变分信息瓶颈(VIB) ^[4] 和我们的一篇在NeurIPS'20上发表的用IB做推荐系统纠偏的工作 ^[5] 。并且，这个发现也启发了我们，信息论作为一门深厚的科学，是不是能在深度学习时代再放异彩？

挑战：表征信息 v.s. 权重信息

Tishby的信息瓶颈是在表征上度量信息，而表征的计算则受到很多网络中间架构的影响。因为大部分的网络都是一种多层的嵌套形式，比如 f(f(f(X)\dots) ，表征 T 则具体值则受到如激活函数，batchnorm，dropout等等操作的影响。18年的一篇文章 ^[6] 就在这个方面开撕，他们的实验中发现当我们把tanh激活函数换成ReLU之后，上面提到的记忆-遗忘现象直接消失了！而且，他们还做了不少实验，最后得出一个结论

压缩的网络可能会也可能不会很好地泛化，未压缩的网络也是如此。

基本等于说信息瓶颈的观点是错误的了。面对这种攻击，Tishby本人也下场battle，可以在这

观看当时的直播回放。

那么，我们能不能选择度量一个 不受中间操作影响 的东西呢？如果神经网络可以表达为一个编码器 T=f(X;\theta) ，其实网络的学习到的权重 \theta 可能才是网络更本质的东西。

基于这个思想，我们认为度量网络 权重中的信息量 会有帮助，至少它应该不会受到激活函数选择的直接影响。

权重信息量和神经网络的PAC-Bayes泛化能力

其实用权重信息量来度量网络泛化能力已经有一些工作了。最早的相关工作应该是NeurIPS'17的这篇 ^[7] 。作者提了一个PAC-Bayes泛化bound，即

\mathbb{E}_{p(S)}[L(w)-L_S(w)] \leq \sqrt{\frac{2\sigma^2}{n}I(w;S)}

大意是网络的泛化误差被网络权重 w 和数据集 S 之间的互信息所bound住。有了它，我们终于可以开始用权重信息量构建一个新的信息瓶颈了！

基于网络权重的信息瓶颈：PAC-Bayes information bottleneck

我们用权重 w 搭建了一个信息瓶颈：

\max I(w;Y|X,S)-\beta I(w;S)

其中第一项代表了标签信息量，第二项代表了权重对于输入数据集的信息量。我们看到，第一项其实在分类问题中就是我们所用的交叉熵损失，所以其实我们在这可以直接写成

\min L_S(w) + \beta I(w;S)

其中第一项是我们的交叉熵损失。此时，我们可以用这个损失来代替表征信息瓶颈里的 I(T;Y) ，用 I(w;S) 来代替表征信息瓶颈里的 I(T;X) 来看看，"记忆-遗忘"现象是否还存在了。

关于激活函数

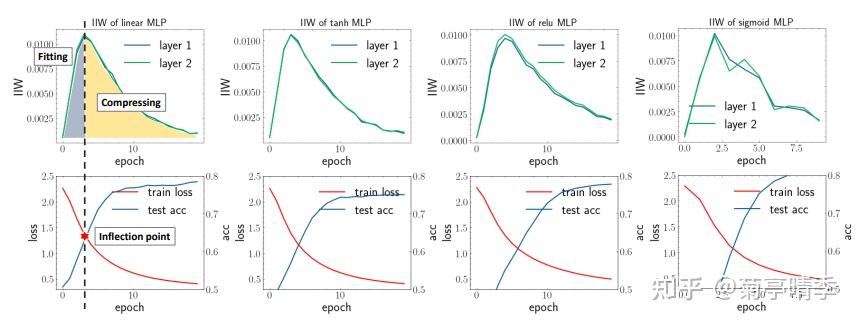
如下图所示，我们选择了四种激活函数，分别是Linear(无激活函数), tanh，ReLU，和sigmoid，并且画出训练损失和度量的information in weight (IIW)，即 I(w;S) 。我们可以看到，所有四个网络都明显的显示出了两阶段的现象：在第一阶段IIW先升高，达到顶点之后进入第二阶段开始下降。并且，可以明显看到，这个IIW的顶点和我们的损失函数值，以及测试精度的拐点基本重合！这是不是说明网络的学习行为和IIW的变化高度一致呢？在记忆阶段，网络也在快速学习；而在遗忘阶段，网络开始"精耕细作"，慢慢地稳步提高。

相对比，在表征信息瓶颈中，只是换了个激活函数（tanh->ReLU），两阶段现象就不复存在。

关于网络层数

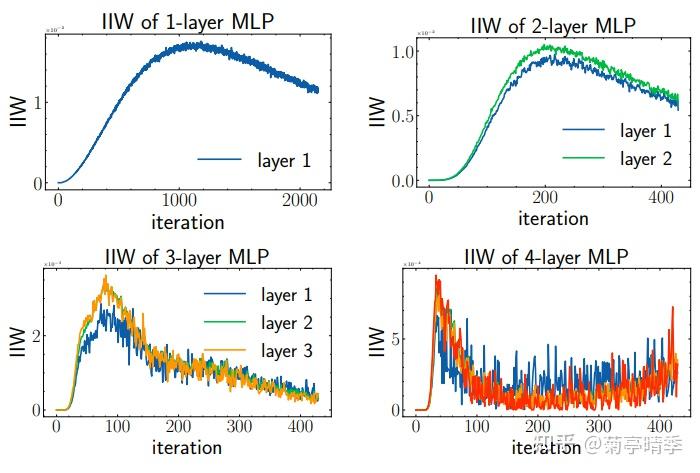
我们进一步来测试下增大网络层数对于IIW有什么影响。下图是1到4层网络的训练情况。我们发现层数越多，IIW达到顶点所需的训练轮数显著减少。比如1层网络需要1000轮左右才达到顶点，而4层网络只花了50轮左右。这说明，增大网络层数能在实践中得到更好效果的原因似乎是其加速了网络对于信息的处理。

关于网络宽度

同样，我们试试加大宽度，看看IIW的变化。下图中我们发现，IIW和不同网络宽度下的网络泛化能力高度同步。比如，在512和4096宽时，网络的泛化误差(generalization gap)，或者说训练精确度减去测试精确度达到最低。同时，IIW也在此时达到最低点。

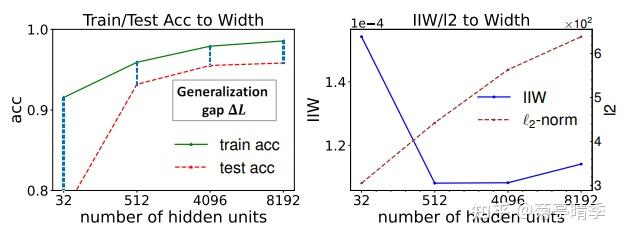
关于网络与批次大小(batch size)

我们继续改变batch size训练网络，并且看看IIW的变化。我们发现在batch size=16的时候，泛化误差达到最小，同时IIW也达到最低点。

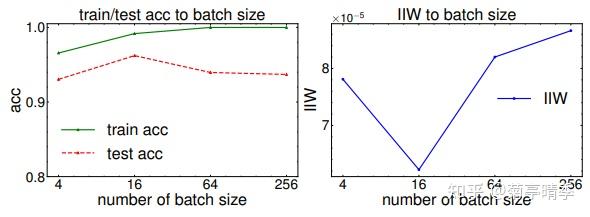
关于信息与数据集噪声程度

我们知道神经网络在过参数(overparameterized)的情况下是可以几乎完全拟合训练集的。那么，IIW在过参数情况下是否继续有效呢？

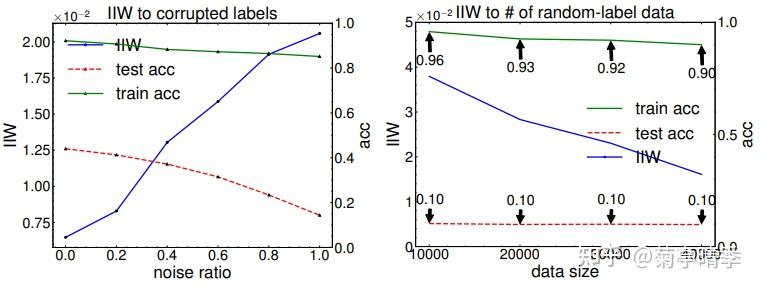
我们首先测试了在噪声逐渐增加的情况下IIW的变化（下左图）。可以看到，在噪声达到100%时，训练精确度仍然稳定在85%，而测试精确度掉到了18%，基本等于瞎猜。这时，我们可以看到IIW也跟着逐渐上升，发现了训练集和测试集的不匹配。哪怕网络能够在100%噪声的训练集上拟合，通过IIW我们也可以看出，网络的泛化能力并不好。

然后，我们测试了下载100%噪声下增加更多的数据（下右图）。可以看到，无论加多少噪声训练数据，测试精确度都稳定在瞎猜10%的水平，这是符合我们的直觉的。同时，由于噪声数据变多，模型拟合训练集的能力也下降了。这也反映在了逐渐降低的IIW上。这说明，哪怕在完全噪声的训练数据的情况下，IIW仍然可以为泛化误差的一个有效度量指标。

小记

我们发现基于权重的信息可以解释很多神经网络的行为，而且我们也可以利用它来指导网络的设计：如果 I(w;S) 就是度量网络泛化误差的量，我们能不能尝试直接优化它呢？这应该是一个有趣的方向。这篇文章里我们做了一些初步的尝试，这里就不再赘述了，感兴趣的朋友可以去看看原文~欢迎讨论~

参考

1. ^ Tishby, N., Pereira, F. C., & Bialek, W. (2000). The information bottleneck method. arXiv preprint physics/0004057. https://arxiv.org/pdf/physics/0004057.pdf?ref=hackernoon.com
2. ^ Tishby, N., & Zaslavsky, N. (2015, April). Deep learning and the information bottleneck principle. In 2015 ieee information theory workshop (itw) (pp. 1-5). IEEE. https://arxiv.org/pdf/1503.02406.pdf?ref=https://githubhelp.com
3. ^ 关于利用 information bottleneck 来解释深度学习 - Zhanxing Zhu的文章 - 知乎 https://zhuanlan.zhihu.com/p/29723280
4. ^ Alemi, A. A., Fischer, I., Dillon, J. V., & Murphy, K. (2016). Deep variational information bottleneck. arXiv preprint arXiv:1612.00410. https://arxiv.org/pdf/1612.00410.pdf
5. ^ Wang, Z., Chen, X., Wen, R., Huang, S. L., Kuruoglu, E., & Zheng, Y. (2020). Information theoretic counterfactual learning from missing-not-at-random feedback. Advances in Neural Information Processing Systems, 33, 1854-1864. https://proceedings.neurips.cc/paper/2020/file/13f3cf8c531952d72e5847c4183e6910-Paper.pdf
6. ^ Saxe, A. M., Bansal, Y., Dapello, J., Advani, M., Kolchinsky, A., Tracey, B. D., & Cox, D. D. (2019). On the information bottleneck theory of deep learning. Journal of Statistical Mechanics: Theory and Experiment, 2019(12), 124020. https://openreview.net/pdf?id=ry_WPG-A-
7. ^ Aolin Xu and Maxim Raginsky. Information-theoretic analysis of generalization capability of learning algorithms. In Advances in Neural Information Processing Systems, pp. 2521–2530, 2017. https://proceedings.neurips.cc/paper/2017/file/ad71c82b22f4f65b9398f76d8be4c615-Paper.pdf