你真的分得清“前后左右”和“东西南北”吗?(二)——经纬度的秘密
早点关注我,精彩不错过!
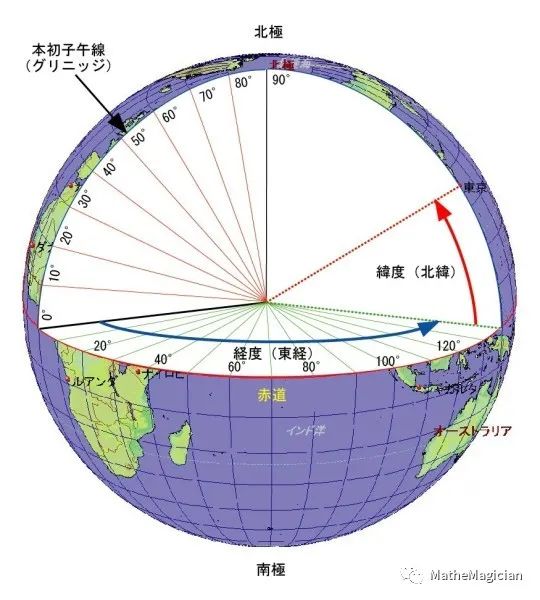
在上一篇文章中,我们聊到了方向的基础,以及地球上描述方向方法选择的两个线索,自转方向基准和球坐标系,相关内容请戳:
你真的分得清“前后左右”和“东西南北”吗?(一)——以太阳还是地球当参考系?
今天我们接着讲。
上期也剧透了这个思路的最终结论即为经纬度的地球上方位描述,我们把球坐标再写一遍:
x = rsintsinp
y = rcostsinp
z = rcosp
经纬度方位之经度
回忆起学过的地理知识和上面的公式,你应该知道了,theta我们叫作为经度,以格林威治天文台为0度起点,其正方向为地球自转的方向。另外,我们知道,有方向的圆周角是一个随旋转运动2pi弧度为周期的值,任何一个长度为2pi的周期都可以代表这个角度的范围。为了不让这个角度的绝对值超过pi,也就是180度,我们取的代表范围是[- pi, pi],可以看作一个模2pi加法群减pi的一个完全剩余系,其特点是整个区间关于原点对称。在大于0度的范围内,绝对值增大表示正方向,小于0度的范围内,绝对值增大其实是数值减小,也就是负方向。
注意到,我们这边的角度,实际上对应的是以原点为公共顶点o,向参考位置s和描述位置d的有向角sod,从os到od,和规定方向相同为正,否则为负。注意这样定义下来,我们常说的角有大角和小角,恰好是起点和终点两个排列形成,在这里恰好一正一负,互为相反数,且都在[- pi, pi]内可以取到。
最后,把取正数的角度称作东经,负值的角度称作西经。显然这里的东经西经其实抛开文化讲,不过也是广义的物理上用正负来表达相对方向的一个实例罢了,它和把一条数轴上原点正方向上的点规定为正数,反方向规定为负数是一个意思。
以此相对地球球心的经度方位定义好以后,两个地球上的点的相对经度方向也可以推导出来了。这一点理解了的的话,就再也不要去背那些如何根据两个经纬度去算谁在谁的东边还是西边多少度的公式了。给定两个点的经度A, B,把西经用加负号替代,则A一定比B大A - B,即A一定在B的东边A - B度。注意,这里的减法,是模2pi加法这个群的操作,而且用来代表群内元素的值取自[- pi, pi],相当于你得把答案通过mod(2pi)减法运算得到值,再等价到[- pi, pi]这个空间去。这样映射有个好处,就是两点的距离绝对值不会超过pi,即通常规定角度取pi以内的值。而不超过pi的那个度量所代表的的方向才能代表真实的谁比谁大,谁在谁后面(东边)的意思,这个方向恰是其中一点要旋转到达另一点需要的最短距离。因此,如果是正数,A一定在B的东边A - B度;如果是负数,得翻译一下,变成A一定在B的西边- (A - B)度。如果负数不翻译,相当于在东边(2pi + A - B)度,但我们一方面希望绝对位置的度量不要超过180度,相对位置也不要,自然这不是一个常规的叫法了。故我们是直接凭借两个位置形成的这个小角的方向,判断谁在谁的哪一侧,具体而言就是看起点B走到A到底是要向东还是向西最近,这和最后得到的旋转正负值,也就是东还是西就一一对应了。
所以东西的概念其实和用+表示和正方向相同,-表示相反没什么区别。而所谓正方向,取的是地球自转的方向,即随着想象的时间推移着,方向跟着前进的方向。而和直线上位置运算的区别是,角度的加减法的结构是mod(2pi)的群,其上两点最大距离为pi,只不过区分正负,也分别叫作在东边和在西边。这样的好处是,无论是描述一个点的绝对位置还是两个点的相对位置,可以用小范围[0, pi]内的绝对值来表达,同时是否为负,也就是是否是西侧,决定其到底是在西还是东的基本属性,也表明了达到终点最近的路到底该朝哪边走,这些方便的判断结论,都源自精妙的数学模型表示的结构设计。
经纬度方位之维度
维度的规定和经度如出一辙,就对应上述角度phi。因为已经有一个2pi范围的平面了,所以phi的整体范围只有pi长,剩下一半通过加180度经度去表示。自然地取右手系的oz方向作为正方向,反方向为负方向就是范围为[- pi / 2, pi / 2]的维度范围了,因为规定的旋转面恰好在范围中间,因此恰好正负各半,符合原来经度想要用更小的数表达距离,符号可代表方向的原则。但是,纬度度和其加法并不构成群结构,比如pi / 2 + pi / 2就超出范围不具有封闭性了,原因就是我们其实只给了一个半球规定了纬度,剩下一半是未定义的,其触达交给经度去实现了。
于是,我们规定正值称为北纬,负值称为南纬,就成了纬度的定义,用减法来衡量其距离的方法还是适用的。假设C,D是两个点的维度,化南纬为负数以后,C - D即表达C比D大的值,如果是正数,即C在D北边C-D度;负数则翻译为C在D南边- (C - D)度,而且这个值绝对值本身就不会超过pi,不需要另外模转化,其值却可以超过任何一个点经纬度的绝对值pi / 2,还是因为在球坐标中,pi方向不是个标准的循环群结构,只用了一半。要用全部不是不行,那经度就得只用一半而已,否则存在一个位置两个描述的非一一映射情况了,这个事已经因为经度比维度的定义先来后到给定下来了,也符合一般的球坐标系的约定。
值得一提的是,在一般的球坐标的定义中,phi定义为以oz为0度起点,范围为[0, pi],而我们这里是以xoy平面内的投影射线为0度起点,范围恰好变得对称,是原来角度减pi / 2。这里可以看到,在地理中,为了使得角度的绝对值范围变小,且可以以之符号有更加明确的物理意义。这样一来,到底是在南半球,还是北半球,到底是在西边还是东边这样重要的信息就被直接地提取出来,可见一个学科的命名习惯其实也是依照其数学模型所需要描述的问题去在原始数学上去做了适配和调整的。
有两点还需要说明一下,这里我简单的用右手系来确定了oz的方向,源于我们日常默认的空间直角坐标系一般就是右手系,是一种约定俗成的习惯,是一种为说明问题的“不妨设”。如果用左手系,以上负号和正号倒转过来即可。还有,我们把北和正联系在一起,使得大天朝恰好在正的维度上,也可以看作一种上,地图上就是这样体现的。而实际上,澳大利亚人却把南看作上,也认为自己在地球的上边,是正方向,用的左手系了,只不过南北半球的人还好对南北的定义是重合的,还是能交流,哪怕心里对正方向的看法完全相反,也都选取了自己土地在正方向上的极坐标手性,去看看澳大利亚南向上的地图就自然明白了。另外,可能一开始定义这些经度,维度的人真的没想我这么多,就直接给本来是通用的数学里的正负的意义取了东西,南北的定义,但我这么分析一边的价值在于,看到这些约定中背后统一的数学逻辑,和妥协的一些人类文化的影子,并分别来欣赏,吸收。
结语和预告
所以,你现在知道为什么地球自西向东转了吧?是因为我们以东为自转方向,在我们说明里就是以自转方向为正方向,规定为东,那可不就是自西向东转么?这个结论几乎就是一条规定而已,并不是什么高深发现,却是智慧。
所以你也应该知道,为什么太阳从东方升起了吧?因为你跟着地球自转一起向一个方向转并且以慢慢地从黑夜进入白天定义为太阳升起,这个过程相当于你从远日点逐渐转到近日点,逐渐的到达午时那个近似的最近日点的过程。因此,相当于你在不断地接近那个点,而你朝哪里转,你便能接近在你哪个方向的点而已。你都规定了地球是向东转的,那太阳不就看起来从东方升起,慢慢地升到头顶你就相当于到达了东方?你要是规定地球是向X转的,那太阳一样也要从X方升起,这同样也是一条基本就是规定的知识,若不知道来龙去脉,还真等于没学过地理。
以上就是我们人类争论了很多年以后,所好不容易统一的描述一个地球上位置的方案。至少概念上统一了,这就很不容易了,虽然不同的语言还是用了如东南西北和“NEWS”这样不同的语言符号来表达。在数学和物理人看来,这不过是在地球上的一次建立球坐标系的实例,然而这种思维可不仅仅存在于地球上,我们还有很多通用的来构建坐标,表明方位的技巧,以及,当你在地球上行走时,也会发现东南西北的局限性,且听我下回慢慢道来。

我们是谁:
MatheMagician ,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖 互联网,计算机,统计,算法,NLP 等前沿的数学及应用领域;也包括 魔术思想,流程鉴赏 等魔术内容;以及结合二者的 数学魔术 分享,还有一些思辨性的谈天说地的 随笔 。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流!
