Kaggle数据竞赛:泰坦尼克号幸存预测 ——基于SPSS Statistics&Modeler
Titanic: Machine Learning from Disaster是Kaggle上最知名的数据科学竞赛之一。该竞赛要求参赛者从训练数据集(train)从得出哪种类型的人群能在事故中更可能存活,并预测测试集(test)中乘客的存活状况。我尝试使用SPSS Statistics&SPSS Modeler来对数据进行整理分析和预测。
一、 数据说明和整理
首先将训练数据集train导入SPSS Statistics中。

可以看出该数据集共有12个变量,各变量说明如下。
PassengerId:对乘客进行标识的ID
Survived:存活情况,1为存活,0为死亡
Pclass:客舱等级,1为高级,2为中级,3为低级
Name:乘客名字
Sex:乘客性别
Age:乘客年龄
SibSp:在船上兄弟姐妹数及配偶数量
Parch:在船上父母及子女数量
Ticket:船票编号
Fare:船票价格
Cabin:客舱区域
Embarked:登船港口
首先对变量进行初步处理,对所有变量增加标签,为了方便数据处理,将变量Pclass、Sex、Survived更改为数值型变量,测度不变。对部分变量的缺失值进行转变。

数据集train共有12个变量,变量Pasenger ID对数据分析没有帮助,可对数值型变量Sex、Age、Pclass、Fare、Parch、SibSp逐个分析对Survived的影响。一些字符串变量如Name、Cabin、Embarked、Ticket比较复杂,无法简洁的转变为数值型变量,只对数值型变量进行分析。
二、 数据处理、可视化及分析
总所周知,在Titanic海难救援中,妇女和小孩先走,年龄大的尽量后走。变量Sex和Age可能是对存活情况影响较大的变量。

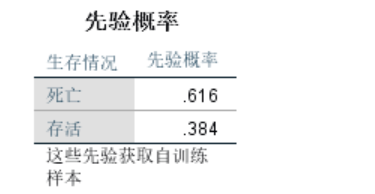
由图可知,在数据集train中,乘客的存活率仅为38.4%
1、 变量Sex对存活率的影响

对变量Sex进行的描述性统计分析显示,变量Sex并无缺失值。总人数891人,男性577人,女性314人。
使用堆积条形图对变量Sex与Survived的关系进行可视化。

再使用简单条形图进行可视化。

选择个案,使得变量Sex=1,即选择所有女性乘客。


选择个案,使得变量Sex=0,即选择所有男性乘客。


由图可知,女性乘客的存活率为74.2%,男性乘客的存活率仅为18.9%。可见“女士优先”这一准则在这一灾难救援中展现的淋漓尽致。
2、 变量Age对存活率的影响
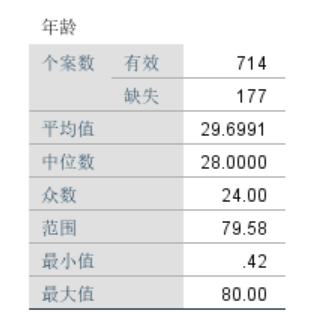
对变量Age进行描述性统计分析的结果显示,变量Age存在177个缺失值,中位数为28,均值为29.70,众数为24。
对变量Age进行缺失值分析。由于样本数较大,且变量Age近似服从正态分布,可考虑使用EM法插补缺失值。



使用均值26.70(保留小数点后两位)对缺失值进行插补。

在对变量Age插补缺失值的情况下可以得出,年龄8岁以下孩子的存活率较高,大于50%;年龄60岁以上的存活率极低;年龄17岁到30岁、37岁到48岁之间的存活率也比较低。
3、 变量Fare对存活率的影响

对变量Fare进行描述性统计分析的结果显示,变量Fare不存在缺失值,均值为32.20,中位数为14.45,众数为8.05,最大值为512.33。

由图可知,变量Fare较高时,存活率也比较高;Fare较低时存活率很低。大体上,Fare越高,存活率也越高。
4、 变量Pclass对存活率的影响
对变量Pclass进行描述性统计分析。


由图可知,客舱等级越高,存活率越高。分析客舱等级是因为,有些乘客的票价相等但是客舱等级不同,这样对他们的存活率或许是有影响的。
5、 变量Parch对存活率的影响
对变量Parch进行描述性统计分析。


当变量Parch为0时,乘客的存活率约为35%,低于所有人的存活率(38.4%);变量Parch为1到2时,乘客存活率大于50%,明显较高;变量Parch大于3时,乘客的存活率极低。
6、 变量SibSp对存活率的影响
对变量SibSp进行描述性统计分析。


很明显,当变量SibSp=0时,乘客的存活率较低,约33%左右,低于所有乘客的存活率(38.4%);SibSp为1或2时,乘客的存活率在50%左右,相对较高;SibSp大于等于3时,存活率极低。
三、 建立模型及预测
1、 使用Statistics建立预测模型
常见的分类与预测模型有回归分析、决策树、人工神经网络、贝叶斯网络、支持向量机等。这里我采取决策树模型。
决策树模型最常见的算法为有CHAID算法、CRT算法、Quest算法、C5.0算法。使用SPSS Statistics建立决策树模型,采取CRT算法。
对数据集train使用决策树模型,最后将输出规则,即决策树算法,进行保存。


最后得到以下结果。





可见对于预测集,该模型在分类预测时,对死亡的预测的正确率为88.2%,对存活的预测的正确率为71.9%,总的正确率81.9%。还显示了在该模型中,自变量的重要性中,变量Sex最大,为0.14;变量Fare的重要性为0.062;变量Pclass的影响为0.047;变量Age的重要性为0.036;变量SibSp的重要性为0.023;变量Parch的重要性为0.021。
读取test数据集,运行刚才保存的决策树语法,得到预测数据。

将数据上传Kaggle得到分数为0.77511。

2、 使用SPSS Modeler建立预测模型
使用SPSS Modeler建立决策树模型,使用C5.0算法。

决策树C5.0模型设置如下。

运行“分析”节点得到以下结果。

运行“表格”节点可得到以下结果。

上图中,SPSS Modeler在建模时,一部分数据用来训练数据,一部分用来测试数据,用来保证模型的可靠性。训练数据和测试数据的分区是随机的。
接下来用生成的模型预测test数据集。

得到以下数据。

将数据上传到Kaggle,得分0.78468。

使用SPSS Modeler还可以建立其他的模型如CHAID、CRT、贝叶斯网络、人工神经网络、随机森林等模型,就不详细说了。

最终,使用SPSS Modeler预测的结果在Kaggle上的成绩如下图。

四、 结束语
总体上来说,对于 Titanic: Machine Learning from Disaster 这一课题来说,SPSS Statistics 和 SPSS Modeler 还是可以做出一定精度的预测的。不过还是有一些局限性的,主要在于对于一些存在缺失值的变量的分析上,可能会损失一些关于存活可能性的信息量。而且对于一些可能隐藏着存活信息的变量,如Name、Cabin等信息,不太容易进行方便的处理
。最后,鉴于我的水平有限,一定还有一些需要改进的地方,请大家指点。

