平抛运动与斜面结合

平抛运动与斜面相结合的模型，其特点是做平抛运动的物体落在斜面上，包括两种情况：
(1)物体从空中抛出落在斜面上；
(2)从斜面上抛出落在斜面上。
在解答该类问题时，除要运用平抛运动的位移和速度规律外，还要充分利用 斜面倾角 ，找出斜面倾角同位移和速度的关系，从而使问题得到顺利解决。

两种常见的情况分类
1、分解速度类

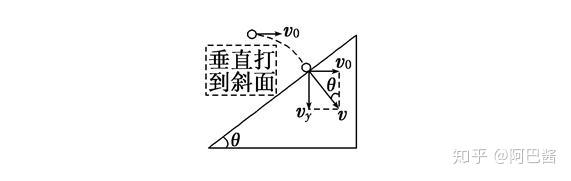
水平速度

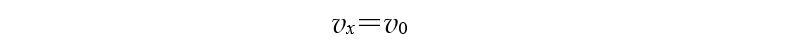
竖直速度

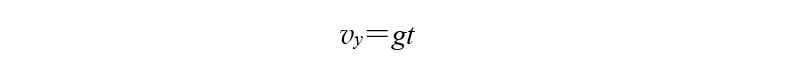
合速度

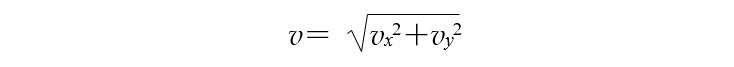
根据上图中的关系

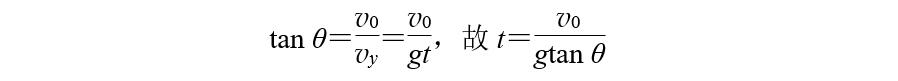
2、分解位移类

水平位移

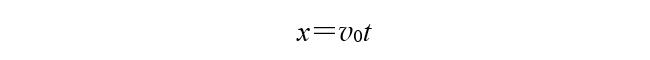
竖直位移

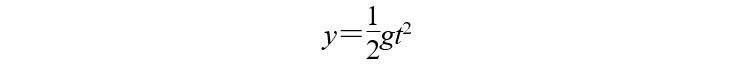
合位移

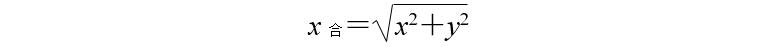
根据上图中的关系

举例分析
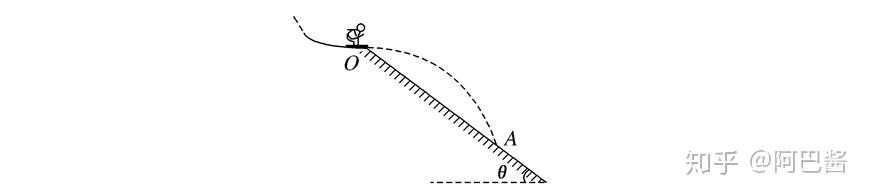
【题目】 滑雪比赛惊险刺激，如图所示，一名跳台滑雪运动员经过一段加速滑行后从 O 点水平飞出，经过3.0 s落到斜坡上的 A 点。已知 O 点是斜坡的起点，斜坡与水平面的夹角 θ ＝37 °，运动员的质量 m ＝50 kg。不计空气阻力。(取sin 37°＝0.60，cos 37°＝0.80； g 取10 m/s2)求：

(1) A 点与 O 点的距离 L 。
(2)运动员离开 O 点时的速度大小。
(3)运动员从 O 点飞出开始到离斜坡距离最远所用的时间。
【分析】 (1)运动员在竖直方向做自由落体运动，有

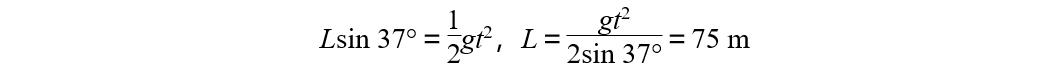
(2)设运动员离开 O 点时的速度为 v 0，运动员在水平方向的分运动为匀速直线运动，有

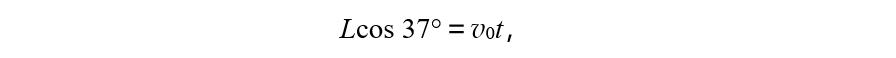
即有

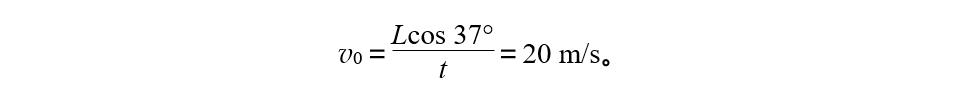
(3)法一：运动员的平抛运动可分解为沿斜面方向的匀加速运动(初速度为 v 0cos 37°、加速度为 g sin 37°)和垂直斜面方向的类竖直上抛运动(初速度为 v 0sin 37°、加速度为 g cos 37°)。
当垂直斜面方向的速度减为零时，运动员离斜坡距离最远，有 v 0sin 37°＝ g cos 37°· t ，解得 t ＝1.5 s。
法二：当运动员的速度方向平行于斜坡或与水平方向成37°时，运动员与斜坡距离最远，有gt/vo＝tan 37°， t ＝1.5 s。
核心要点(1)物体在斜面上平抛并落在斜面上的问题，一般要从位移角度找关系，该类问题可有两种分解方法：一是沿水平方向的匀速运动和竖直方向的自由落体运动；二是沿斜面方向的匀加速运动和垂直斜面方向的类竖直上抛运动。(2)物体平抛后垂直落在斜面上的问题，一般要从速度方向角度找关系。
【题目】 一水平抛出的小球落到一倾角为 θ 的斜面上时，其速度方向与斜面垂直，运动轨迹如图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为( )

【分析】 小球在竖直方向下落的距离与水平方向通过的距离之比即为平抛运动合位移与水平方向夹角的正切值。小球落在斜面上速度方向与斜面垂直，故速度方向与水平方向夹角为Π/2－ θ ，由平抛运动结论：平抛运动速度方向与水平方向夹角正切值为位移方向与水平方向夹角正切值的2倍，可知：小球在竖直方向下落的距离与水平方向通过的距离之比为（1/2）tan(Π/2－ θ )＝1/2tanθ
我是方哥一个不太出名但是又有点理想的物理老师点个关注，你我缘分就此开始