根据两地经纬度计算两地距离的各种方法与公式
在网络上搜索了一下, 根据两地经纬度计算两地距离几乎找不到像样的推导,本篇文章利用本人想到的三种方法来推导计算公式,给出5种正确的结果,网络上其他人直接给出的结果均没有逃出我推出的5个结果 。欢迎读者收藏阅读。
为了与数学中的惯例保持一致,本文我们将西经看作负值,东经看作正值,北纬看作负值,南纬看作正值。则纬度的取值范围是 [-\frac{\pi}{2}, \frac{\pi}{2}] , 经度的取值范围为 [-\pi, \pi] . 当然,正负可以根据个人喜好随意规定,并不会影响最终的计算结果。
- 经纬度与空间直角坐标系的变换关系
- 在三维直角坐标系中利用向量内积来计算
- 在三维直角坐标系中利用勾股定理来计算
- 在等腰梯形里计算
- 距离公式的总结
1. 经纬度与空间直角坐标系的变换关系
假定地球半径为 R , 对于地面上的任意一点,假定其纬度与经度分别为 \theta, \varphi , 则转化到三维空间直角坐标系有
\left\{ \begin{array}{c} x=R\cos\theta\cos\varphi \\ y=R\cos\theta\sin\varphi \\ z=R\sin\theta \end{array} \right.
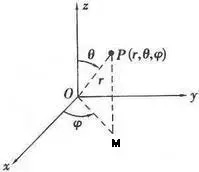
2. 在三维直角坐标系中利用向量内积来计算
很多传统几何问题用向量方法去处理都会简单很多,因为向量方法将很多思想转化为了计算。正如同 n 元一次方程能够解决的问题使用向量均可以解决一样,但是方程将很多思维转换成了计算。
计地心为 O , 地面上的 A 点的纬度与经度分别为 \theta_{1}, \varphi_{1} , B 点的纬度与经度分别为 \theta_{2}, \varphi_{2} , 在空间直角坐标系中的坐标分别为 (x_{1}, y_{1}, z_{1}), (x_{2}, y_{2}, z_{2}) , 则
\cos\angle AOB=\frac{x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}}{R^{2}} \\ =\cos\theta_{1}\cos\varphi_{1}\cos\theta_{2}\cos\varphi_{2}+\cos\theta_{1}\sin\varphi_{1}\cos\theta_{2}\sin\varphi_{2}+\sin\theta_{1}\sin\theta_{2} \\ =\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})
则
S=R\angle AOB=R\arccos(\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1}))
3. 在三维直角坐标系中利用勾股定理来计算
计地心为 O , 地面上的 A 点的纬度与经度分别为 \theta_{1}, \varphi_{1} , B 点的纬度与经度分别为 \theta_{2}, \varphi_{2} , 在空间直角坐标系中的坐标分别为 (x_{1}, y_{1}, z_{1}), (x_{2}, y_{2}, z_{2}) , 则根据勾股定理有
AB=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}} \\ =R\sqrt{(\cos\theta_{2}\cos\varphi_{2}-\cos\theta_{1}\cos\varphi_{1})^{2}+(\cos\theta_{2}\sin\varphi_{2}-\cos\theta_{1}\sin\varphi_{1})^{2}+(\sin\theta_{2}-\sin\theta_{1})^{2}} \\ =R\sqrt{2-2\sin\theta_{1}\sin\theta_{2}-2\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{1}-\varphi_{2})}
因此
\sin^{2}\frac{\angle AOB}{2}=(\frac{AB}{2R})^{2}=\frac{1-\sin\theta_{1}\sin\theta_{2}-\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2} \\ \cos^{2}\frac{\angle AOB}{2}=1-\sin^{2}\frac{\angle AOB}{2}=\frac{1+\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2}
则
\cos\angle AOB=\cos^{2}\frac{\angle AOB}{2}-\sin^{2}\frac{\angle AOB}{2}=\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})
因此两地距离
\left\{ \begin{array}{c} S=R\angle AOB=R\arccos(\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})) \\ S=2R\frac{\angle AOB}{2}=2R\arcsin(\sqrt{\frac{1-\sin\theta_{1}\sin\theta_{2}-\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2}}) \\ S=2R\frac{\angle AOB}{2}=2R\arccos(\sqrt{\frac{1+\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2}}) \\ \end{array} \right.
4. 在等腰梯形里计算
如图,假定 A, B, C, D 为地球表面上四点, A 点的纬度与经度分别为 \theta_{1}, \varphi_{1} , B 点的纬度与经度分别为 \theta_{1}, \varphi_{2} , C 点坐标为 \theta_{2}, \varphi_{2} , D 点坐标为 \theta_{2}, \varphi_{1} , 则四边形 ABCD 为等腰梯形。
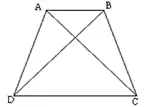
现在我们要算的是 A, C 两点之间的距离 S , 显然
\left\{ \begin{array}{c} AB=2R\sin\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1} \\ AD=BC=2R\sin\frac{\theta_{2}-\theta_{1}}{2} \\ CD=2R\sin\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{2} \end{array} \right.
由余弦定理在 \triangle ABC 有
AC^{2}=AB^{2}+BC^{2}-2AB\cdot BC\cos\angle ABC \\ =4R^{2}\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos^{2}\theta_{1}+4R^{2}\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}-8R^{2}\sin\frac{\varphi_{2}-\varphi_{1}}{2}\sin\frac{\theta_{2}-\theta_{1}}{2}\cos\theta_{1}\cos\angle ABC
同理,在 \triangle ACD 中
AC^{2}=AD^{2}+CD^{2}-2AD\cdot CD\cos\angle ADC \\ =4R^{2}\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos^{2}\theta_{2}+4R^{2}\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}-8R^{2}\sin\frac{\varphi_{2}-\varphi_{1}}{2}\sin\frac{\theta_{2}-\theta_{1}}{2}\cos\theta_{2}\cos\angle ADC \\ =4R^{2}\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos^{2}\theta_{2}+4R^{2}\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}+8R^{2}\sin\frac{\varphi_{2}-\varphi_{1}}{2}\sin\frac{\theta_{2}-\theta_{1}}{2}\cos\theta_{2}\cos\angle ABC
联立以上两式消去 \cos\angle ABC 可得
AC^{2}=4R^{2}\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}+4R^{2}\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}
则
\sin^{2}\frac{\angle AOC}{2}=\frac{AC^{2}}{4R^{2}}=\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}+\sin^{2}\frac{\theta_{2}-\theta_{1}}{2} \\ \cos^{2}\frac{\angle AOC}{2}=1-\sin^{2}\frac{\angle AOC}{2}=\cos^{2}\frac{\theta_{2}-\theta_{1}}{2}-\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}
则
\cos\angle AOC=\cos^{2}\frac{\angle AOC}{2}-\sin^{2}\frac{\angle AOC}{2}=\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})
与第一种方法得出相同的结果。因此同样有
S=R\angle AOC=R\arccos(\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})) \\ S=2R\frac{\angle AOC}{2}=2R\arcsin(\sqrt{\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}+\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}}) \\ S=2R\frac{\angle AOC}{2}=2R\arccos(\sqrt{\cos^{2}\frac{\theta_{2}-\theta_{1}}{2}-\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}}) \\
4. 距离公式的总结
综合上述推导过程,我们罗列出以下5个正确结果
\left\{ \begin{array}{c} S=R\arccos(\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})) \\ S=2R\arcsin(\sqrt{\frac{1-\sin\theta_{1}\sin\theta_{2}-\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2}}) \\ S=2R\arccos(\sqrt{\frac{1+\sin\theta_{1}\sin\theta_{2}+\cos\theta_{1}\cos\theta_{2}\cos(\varphi_{2}-\varphi_{1})}{2}}) \\ S=2R\arcsin(\sqrt{\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}+\sin^{2}\frac{\theta_{2}-\theta_{1}}{2}}) \\ S=2R\arccos(\sqrt{\cos^{2}\frac{\theta_{2}-\theta_{1}}{2}-\sin^{2}\frac{\varphi_{2}-\varphi_{1}}{2}\cos\theta_{1}\cos\theta_{2}}) \\ \end{array} \right.
根据上述推导过程,很容易知晓这5个结果是相等的,读者也可以自行验证。

