收入时间序列——之预测总结篇

本章节分两部分，一是ARMA模型预测，另一个是LSTM模型预测。过程中会结合数学原理探求本质，以便理解两个模型拟合效果的比较。

一. ARMA模型预测

我们对模型arimatest=ARIMA(2,0,4)×(1,1,1,7)进行拟合后，做向前7步预测：

> # 预测
> fc<-forecast(arimatest,h=7,level=c(99.5))
         Point Forecast   Lo 99.5  Hi 99.5
162.1429       36285.83 -37121.33 109693.0
162.2857       49331.44 -38293.45 136956.3
162.4286       38016.79 -52834.00 128867.6
162.5714       37847.55 -54204.97 129900.1
162.7143      113477.48  20428.50 206526.5
162.8571      110839.43  17751.50 203927.4
163.0000       38841.40 -54396.23 132079.0

上述输出结果左边第一列Point值是将原序列按周排序，第一天是2015-9-30，位于2015年第39周的周三，样本内最后一天是2018-2-5，位于第162周的周一。因此样本外的第一天位于第162周的周二，即2018-2-6，所以根据frequency=7，系统自动将每一周切分成7份，看到的就是小数了。

注意，它和predict方法效果一样：

> # 预测
> pred<-predict(arimatest,7)
$`pred`
Time Series:
Start = c(162, 2) 
End = c(163, 1) 
Frequency = 7 
[1]  36285.83  49331.44  38016.79  37847.55 113477.48 110839.43  38841.40
Time Series:
Start = c(162, 2) 
End = c(163, 1) 
Frequency = 7 
[1] 26151.15 31216.19 32365.40 32793.52 33148.51 33162.38 33215.72
> accuracy(pred$pred,test_income[1:7])
                ME     RMSE      MAE       MPE     MAPE
Test set -20273.42 32945.89 22699.64 -46.34546 51.47128

我们看看样本外真实数据的实际对比：

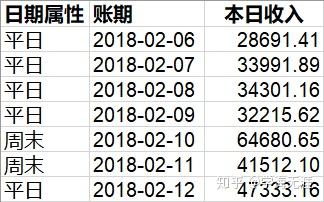
模型拟合的值偏高，这是因为这周正好赶在春节前一周，可能对收入产生一定影响（负向扰动），均方根误差为32945元，说明误差很大，模型拟合的并不够好，很多波动因素没有考虑进去。我们再用图形直观地看下：

# 比较
ts.plot(test_income[1:7], pred$pred, lty = c(1,3))
abline(reg=lm(test_income[1:7]~pred$pred))

从上图看出，向前4步的预测效果都比较好，第5/6步预测（周末2天）预测偏差较大，实际值明显偏低，第7步预测也比较好。

我们再看下向前30步预测：

很明显，超过7天的预测效果较差，这是由两方面原因来解释：其一是因为我们的ARIMA模型是一个季节模型，预测也会呈现明显的7天周期性，同时根据ARMA预测模型的理论，向前预测的估计值就是数学期望（条件无偏最小方差估计），且预测的方差（置信区间）随预测步长增加也会越来越大，所以只适合短期预测，不过可以通过动态（修正）预测来进行改善；其二是因为模型只提取了线性部分，对扰动没有考虑，之前文章已验证它并不是正态随机波动，而是有明显的ARCH效应，所以这样的扰动不能被忽略，比如上图中第二个7步预测正好是春节期间，所以收入有一个明显增长（正向扰动）。

为了得到更强有力的预测结论，利用交叉验证的方法，将原序列860天数据拆分成不同的训练集和验证集，其中训练集包含90天数据，验证集是紧随其后的7天数据，然后不断往前平移30天，得到25组数据集。R代码如下：

# 样本重新取样，交叉验证
library(rsample)
periods_train <- 90
periods_test  <- 7
skip_span     <- 30
ro_resamples <- rolling_origin(
  data,
  initial    = periods_train,
  assess     = periods_test,
  cumulative = FALSE,
  skip       = skip_span)
win.graph(width = 10,height = 10,pointsize = 8)
par(mfcol=c(5,5))
for(i in 1:dim(ro_resamples)[1]){
  ro1_train<-analysis(ro_resamples$splits[[i]])
  startW <- as.numeric(strftime(head(ro1_train$账期, 1), format = "%W"))
  startD <- as.numeric(strftime(head(ro1_train$账期, 1), format =" %w"))
  ro1_train_data = ts(ro1_train$本日收入, frequency = 7,start = c(startW, startD))
  ro1_test<-assessment(ro_resamples$splits[[i]])
  startW_test<-(end(ro1_train_data)[1]*7+end(ro1_train_data)[2]+1)%/%7
  startD_test<-(end(ro1_train_data)[1]*7+end(ro1_train_data)[2]+1)%%7
  ro1_test_data = ts(ro1_test$本日收入, frequency = 7,start = c(startW_test, startD_test))
  # autoarima = auto.arima(ro1_train,trace=F)
  # print(autoarima$arma)
  # print(autoarima$aic)
  arimafit<-arima(ro1_train_data,order=c(1,0,2),seasonal=list(order=c(1, 1, 1),period=7))
  pred<-predict(arimafit,7)
  par(new=F)
  ts.plot(ro1_test_data, pred$pred, lty = c(1,3), col=1:8)
}

25组数据用同一ARIMA季节模型的7天预测效果如下：

设置平移10天，得到70组，7天预测效果如下：

设置平移45天，得到17组，7天预测效果如下：

红色曲线表示向前7步预测，黑色曲线为验证集7天数据，可看出不论设置的平移天数是大是小，大部分情形下模型都能捕捉预测到其趋势走向，有的7天预测效果非常好，有的则稍差一些。总的来说，通过这些分析，我们可得出以下结论：

门店日收入是一个以 7 天为周期的季节性生意，是非平稳的，经季节差分调整的序列平稳，它包含一个线性平稳模型，以及一个不稳定的波动（条件异方差）模型，且波动不是一个线性模式，这样的波动或扰动从业务上解释就是通常发生在节假日，当然也包括其它情形，比如门店人为因素、天气因素、经济环境因素等等，而且它还很可能是非对称或时间不可逆的，即增长和下降幅度并不相同。

二. 非线性模型

以上，让我们开始重新思考，考察原序列的分布是否满足独立同分布（IID，iid或i.i.d.，Independently and Identically Distributed），IID是机器学习领域的重要假设，它要求训练数据和测试数据是满足相同分布的，这是使得训练数据获得的模型能够在测试集获得好的效果的一个基本保障。

主要通过散点图和BDS检验两种方法。散点图是看序列和过去延迟阶序列的二维联合分布是否为正态（椭圆形云状），BDS检验是将序列和过去延迟阶序列作为一个点投影到向量空间，延迟一阶就是二维，延迟两阶就是三维，如果独立同分布，则满足高维空间的相关性求和应该是低维空间相关性求和的幂乘关系，这里定义的相关性求和实质是两个点的距离小于给定参数 \delta 的点对数目的期望极限。

我们绘制日收入序列的自相关12阶延迟的散点图，选12阶是因为运行ar函数系统根据AIC给出的自回归阶数：

# ar函数查看滞后阶
ar(income_data,method = 'mle')$order
# IID独立同分布检验
win.graph(width = 10,height = 10,pointsize = 8)
lag.plot(income_data,lags = 12)

如果是独立同分布，尤其针对二元正态分布，其散点图形状应该呈现一个椭圆，此处很明显数据是非正态的，则相关过程也必然是非线性的。

再看BDS检验，直接调用R中的bds.test函数：

> iid_result<-bds.test(income_data)
> iid_result
	 BDS Test 
data:  income_data 
Embedding dimension =  2 3 
Epsilon for close points =  24472.58 48945.16 73417.74 97890.32 
Standard Normal = 
      [ 24472.5803 ] [ 48945.1605 ] [ 73417.7408 ] [ 97890.3211 ]
[ 2 ]        29.9547        24.5187        20.8156        19.5068
[ 3 ]        32.6452        23.3057        18.5383        17.3194
p-value = 
      [ 24472.5803 ] [ 48945.1605 ] [ 73417.7408 ] [ 97890.3211 ]
[ 2 ]              0              0              0              0
[ 3 ]              0              0              0              0
> iid_result$p.value
  24472.5802675822 48945.1605351644 73417.7408027466 97890.3210703288
2    3.824768e-197    9.343533e-133     3.128022e-96     9.606095e-85
3    9.378948e-234    3.883166e-120     1.014683e-76     3.357185e-67

检验结果在2历史、3历史下p值几乎均为0，拒绝原假设，故不是独立同分布，说明很难用线性模型来拟合，这也与之前做条件异方差分析的结果相合。

为了更清楚的说明非线性模型，这里有必要介绍下面几种：

（一）自激发 SETAR 模型

k 体制表示有 k 个分段函数，每个分段函数都是 p 阶自回归 AR 模式的线性表达式，它最大特点是必须要有一个 d 阶延迟的时刻变量 x_{t-d} 作为门限控制， \gamma_{j} 是门限参数。其缺点是条件均值方程不连续，毕竟它是分段函数，很容易产生间断点。

（二）平滑转移 STAR 模型

\frac{x_{t-d}-\Delta}{s} 实质是对 x_{t-d} 标准化，然后以它作为自变量，施加一个 F 连续函数，这个连续函数特点是值域为 [0,1] 的区间，所以适用的形式可以是Sigmoid函数或分布函数，所以相当于分配了一个0到1之间的权重系数，这就是光滑的来历。其优点是可以直接运用单位根是否在圆内明确时序 x_{t} 的平稳性，缺点是参数 \Delta 和 s 很难估计。

（三）神经网络模型（多层感知机）

每个隐藏层（hidden layer）的一个节点其实都是一个自回归线性表达式的函数，一般称激活函数，比如最常见的Sigmoid函数。在机器学习领域，习惯称 \alpha_{0j} 为偏移bias，称 w_{ij} 为权重，它们都是向量或矩阵。

神经网络模型是半参数模型，激活函数和自回归表达式已知，只需要算出各层的权重和偏移这些参数即可。 计算机方式与数学方式最大区别在于：计算机喜欢用迭代方式解决复杂运算问题，数学喜欢用推理方式解决本质问题。所以最好的解决问题方法就是先理解数学原理，然后用计算机解决。 比如在本例中，我们发现日收入是一个非线性问题，用传统的线性方式预测的精度较低，于是就可以用计算机拟合非线性模型去解决，是一个较好的选择。

三. LSTM模型深入理解

理解LSTM需要先清晰的理解RNN原理，先看下面这个极简的例子，是keras发明者在自己的书中通过一个例子阐述RNN原理，它实现了只有一个隐藏层、一个隐层节点的神经网络：

import numpy as np
timesteps = 100
input_features = 32
output_features = 64
inputs = np.random.random((timesteps, input_features))
state_t = np.zeros((output_features,))
W = np.random.random((output_features, input_features))
U = np.random.random((output_features, output_features))
b = np.random.random((output_features,))
successive_outputs = []
for input_t in inputs:
    output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)
    successive_outputs.append(output_t)
    state_t = output_t
final_output_sequence = np.stack(successive_outputs, axis=0)

上述程序只是示例单个序列，不难看到下述张量及它们的shape：

inputs：[100, 32]，输入张量的样本时序集合，shape[0]=100是时序步长，shape[1]=32是输入特征维度

state_t：[64, ]， 状态张量 ，是一个长度为64的array

W：[64, 32]，输入张量权重，本例中只有正向传播，没有更新

U： [64, 64]，状态张量权重，本例中只有正向传播，没有更新

b：[64, ]，偏移bias，也是一个长度为64的array

input_t：[32, ]， 输入张量 ，是inputs在每一个时刻的输入

output_t：[64, ]， 输出张量 ，shape为[64, ]

对输入张量和状态张量作运算 W\times input\_t+U\times state\_t+b ，相当于 (64,32)\times(32,)+(64,64)\times(64,)+(64,) ，运算的张量结果为 (64,) ，再进行 tanh 激活函数，输出范围为 (-1, 1) 的值域区间，作为output_t，将它作为下一时刻的state_t，然后重复迭代下一个时刻的运算，如此循环，直到input_t时序步长结束。此例中，相当于迭代了100次。

针对这个例子我自己画了一个对应的RNN原理图，对比可看出LSTM原理图的雏形。

上述LSTM原理图是一种逻辑关系图，其实并不有助于理解，因此 我按照神经网络模型的输入层、隐藏层、输出层的形式，重新梳理画了如下图，会更容易理解来龙去脉及性质：

我们作如下深入解释：

（1）三个门控 f_{t} 、 i_{t} 、 o_{t} 分别代表遗忘、输入、输出，它们都是由当前时刻的输入数据 x_{t} 和上一时刻的输出也即hidden state隐藏状态 h_{t-1} ，分别作权重 W 和偏移 b 的线性组合，然后通过 \sigma 激活函数形成，它们的值域均为 [0,1] 。门控可以理解成开关系数，接近 0 表示信息不通过，接近 1 表示信息通过。

（2）一条信息传送带 C_{t} 代表cell state单元状态，也有翻译成细胞状态、神经元状态，这个cell state实际就是整个 LSTM cell 的状态变量。其中与之相关的 \tilde{C_{t}} 表示当前信息，它也是由 x_{t} 和 h_{t-1} 分别作权重 W 和偏移 b 的线性组合，不过它是通过 tanh 函数形成，值域为 [-1,1] 。注意 C_{t} 和 \tilde{C_{t}} 它们都不是门控，它们是 f_{t} 和 i_{t} 两个门控所作用的载体， f_{t} 控制上一个信息 C_{t-1} ， i_{t} 控制本次输入的信息 \tilde{C_{t}} ，综合作用叠加形成新的载体 C_{t} ，所以 C_{t}=f_{t}\cdot C_{t-1}+i_{t}\cdot\tilde{C_{t}} 。上图中只有这条信息传送带我画了一条实线，贯穿整个过程。

（3）最终输出 h_{t} 代表hidden state隐状态。某种程度上虽然也可以将 C_{t} 作为过程的一个输出，但更为重要的、真正意义上的输出只有 h_{t} ，它由输出门控 o_{t} 所控制。因为 C_{t} 是由两部分信息迭代累加，很可能超出一定范围，所以需要用 tanh 函数约束一下值域范围，因此最终的输出也就是新的隐状态 h_{t}=o_{t}\cdot tanh(C_{t}) 。

（4）上述 \cdot 表示的是向量内积，而不要简单看成数量乘关系。实际情况下，输入、状态、输出都是向量形式，权重是矩阵形式，可以结合下面（8）参数一起看以便于理解。

（5） \sigma 和 tanh 性质完全不同， \sigma 是激活函数，值域为 [0,1] ，所以完全充当门控的作用，而 tanh 函数虽然也常作为激活函数，值域为 [-1,1] ，但在此处LSTM中它的作用是控制信息的范围不会溢出。

（6）信息传送带 C_{t} 和输出 h_{t} 的关系就好比运载火箭和飞船（着陆舱）的关系，运载火箭在整个过程中提供动力，飞船和着陆舱才是我们需要的最终结果，飞船执行太空实验任务，着陆舱将宇航员和实验结果带回地球。

（7）红色虚线框代表一个LSTM单元，即LSTM Cell，它接受上一时刻的 h_{t-1} 、 C_{t-1} 和当前时刻的 x_{t} 作为输入，经LSTM单元处理后，得到当前时刻的 h_{t} 、 C_{t} 作为输出，再和下一时刻的 x_{t+1} 一起再次作为输入，重复迭代这样的循环过程，所以说LSTM就是将同一LSTM Cell沿时间展开的RNN，循环迭代多少次呢，就是下面要提到的时间步timesteps，在一个timesteps循环迭代过程中，记忆传送穿过该条样本，并得到记录。

（8）几个重要参数含义：

（8.1）在Tensorflow里，有一个BasicLSTMCell函数，其调用形式为cell = tf.contrib.rnn.BasicLSTMCell( num_units , state_is_tuple )，返回的是LSTM Cell所对应的两个输出 h_{t} 和 C_{t} ：

参数 num_units 字面解释为数量单元，有的地方喜欢用size或hidden_size，字面解释为隐层大小，其实都是一个意思， 表示一个LSTM单元（LSTM Cell）的输出维度 ，结合上面RNN程序示例看出这个维度和权重 W 和 U 、偏移 b 、状态 C_{t} 、输出 h_{t} 的维度都是相一致的，即 num_units=64。 这里顺便提一下共享权重，针对三个门控和一个 \tilde{C_{t}} ，先将 [x_{t},h_{t-1}] concat连接为一个新的向量，其维度等于输入维度加上输出维度，结合上述RNN案例即为32+64=96，然后分别作用于这 4 类共享权重 W ，对应矩阵维度均为 64\times96 。

参数 state_is_tuple 表示是否将两个内部状态 C_{t} 和 h_{t} 作为二元组，设置为 True 表示接受和返回的状态是c_state和m_state的2-tuples，这是官方建议的。若设置为False表示这两个内部状态将按列连接起来返回，尽管目前False是默认值，但它很快要被deprecated。

（8.2）keras进一步封装成LSTM函数，其调用形式为lstm=keras.layers.recurrent.LSTM( units , input_dim, return_sequences, stateful )，返回视参数 return_sequences 而定：

参数 units 和上面num_units一样都是表示 输出维度 ；

参数 input_dim 表示输入维度，当使用该层为模型首层时，应指定该值或等价的指定input_shape，例如shape为(sample, timesteps, input_dim) 或 (batch_size, timesteps, input_dim)的3D张量 ；

参数 return_sequences 表示是否返回每个时间步连续输出的完整序列，设置为True返回shape为 (batch_size, timesteps, output_dim) 的三维张量，默认设置为False仅返回最后一步的输出序列，即shape为 (batch_size, output_dim) 的二维张量。该参数用于多个LSTM层之间的传递；

参数 stateful 表示索引 i 处每个样本的最后状态将被用作下一次批处理中索引 i 处样本的初始状态，而这 对于存在自相关性的时间序列必须设置为True ，否则默认值False会在正常（无状态）模式下，对样本重新洗牌，时间序列与其滞后项之间的依赖关系将会丢失。结合上面的LSTM模型其实就是 C_{t} 是否在下一个batch重新初始化，对于一个完整的时间序列，我们当然不希望也不能重新初始化，否则这条信息传送带将失去应有的作用。

（8.3）如果需要运用多个LSTM Cell，Tensorflow可以用MultiRNNCell(cells)函数，cells是通过BasicLSTMCell实例生成的列表；keras可以用model.add(LSTM(units))来添加多个LSTM层，方法更为简便灵活。

四. LSTM模型预测（一）：框架说明

我们先梳理一下框架：

1. 数据集：我们在原序列860天数据基础上，又补充了135天的时序数据，合并作为原序列。

2. 测试集：上述995天数据拆分为两部分，取20%作为测试集，仅用于预测模型的最终评估。

3. 训练集和验证集：995天数据取80%为训练集和验证集，这其中再取80%用于训练，20%给验证集用于超参数（hyperparameter）调试。

4. 参数 stateful 设置：因为我们在ARMA分析时得知，收入时序的ACF呈现7天自相关性，需要长期记忆，故我们需要设置 stateful=True 。

5. 输入：输入的3D张量(batch_size, timesteps, input_dim)设置为 (256,3,1) ，着重说一下：

input_dim=1：因为只有收入数据，故输入feature维度为1；

timesteps=3：时间步长的设置应该和序列AR阶保持一致，本例中经7步差分后序列的ARMA模型仍存在7天周期的季节AR(1)，以及一个普通的AR(2)或AR(1)，它们之间的作用是交错的，因此时间步长无法简单设置，我们经实际调优后设置为3；

batch_size=256：对于存在条件异方差的序列，batch_size如果选的特别小比如1，则模型更新权重参数的频率很高，振荡严重，效果会很差。经调试后设置为256效果较好，每批次相当于输入8-9个月的样本时序数据，结合前面 stateful 的设置，模型会在每个batch的对应位置样本之间传递 C_{t} 状态信息。

6. LSTM层数：鉴于数据量不算大，一层足够，经调优确实一层效果最好。

7. LSTM状态单元数量：即输出维度，决定模型复杂度，经调优设置为 rnn\_unit=50 最佳。

8. 训练迭代次数：调用EarlyStopping在200轮以内稳定，故设置为 epochs = 150 。

9. 训练的参数数量：我们只添加一个LSTM层和一个全链接dense（密集）层。

LSTM层：对于每个门控 f_{t} 、 i_{t} 、 o_{t} 及传送带状态 \tilde{C_{t}} ，都有 W\cdot\begin{pmatrix} x_{t} \\ h_{t-1} \end{pmatrix}=\begin{pmatrix} W_{x} & U_{h} \end{pmatrix}\cdot\begin{pmatrix} x_{t} \\ h_{t-1} \end{pmatrix}+b ， x_{t} 输入特征维度是 (1,) ， h_{t-1} 输出维度是 (rnn\_unit,) ，偏移 b 维度同输出一致为 (rnn\_unit,) ，故所需要训练的参数共有 rnn\_unit\times(rnn\_unit+1+1)\times4 ，这里要注意的是参数数量和 batch\_size 、 timesteps 均无关系，但每一次 epochs 会重新计算本轮训练的全部参数，每一批次 batch 内会根据输入的样本不断更新这些参数。

dense层：作为最终输出，即预测次日的收入，设置的 units=1 ，它也是经过权值矩阵及偏移的线性计算，再通过激活函数输出，即： activation(input\cdot kernel+bias) ， input 就是上一层LSTM的输出，其维度为 (rnn\_unit,) ， kernel 是权重，本层最终输出为 (1,) ，因此dense层训练的参数数量为 rnn\_unit+1 。

四. LSTM模型预测（二）：原序列

以上是超参数调优结果，似乎我们可以开始编写代码了，但从我之前的文章已获知收入序列是非平稳序列，一个航空模型的特例——没有趋势但有季节特征，如果直接拿这样的时间序列交给模型作预测，无疑增加它的学习负担。实践结果也是如此，经调参后验证集loss值最好成绩为0.05946，相应的测试集RMSE为45154.894，而且在同样的参数下模型表现不稳定，通常情形RMSE值还要更高，下面这个实验结果还是我较早之前做的：

RMSE值高达64268.95，loss值一直趋于平缓不再下降，甚至后一段还上升，产生过拟合：

测试集拟合的预测值与真实值效果比对图：

从图看出，拟合效果欠佳。所以我们需要采取其它手段进一步优化，比如：进行7步季节差分，同时为避免预测值出现负值，对原序列取对数，这样做还有一个好处是能减弱序列的异方差性质，增加正态性，在程序结束部分当然还要对序列进行还原操作。

四. LSTM模型预测（三）：原序列取对数、季节差分

下面开始正式构建代码，我将使用keras框架高效搭建，用François Chollet自己的话说，他写keras的初衷就像乐高玩具一样，提供一个模型架构，组装一下就可以了。

读入数据，先取对数，然后季节差分，最后标准化，这里为了和LSTM中的状态变量值域保持一致，选择的是MinMaxScaler函数将值域控制在[-1,1]之间：

train_data = read_file('A店-每日收入指标跟踪表-训练.csv')
test_data = read_file('A店-每日收入指标跟踪表-测试.csv')
train_data = train_data.iloc[:,1:2]
train_data.columns = ['本日收入']
test_data = test_data.iloc[:,1:2]
test_data.columns = ['本日收入']
# 训练和测试两个数据集合并
data = concat((train_data,test_data), axis=0)
# 取对数
data = np.log(data)
# 7天季节差分
diff_data = data.diff(7)
diff_data.dropna(inplace=True)
# 标准化
scaler = MinMaxScaler(feature_range=(-1, 1))
scaled = scaler.fit_transform(diff_data)

定义超参数，以下是不断调优后的结果：

# 定义超参数
batch_size = 256          # 批数据大小
epochs = 150              # 实验训练次数
rnn_unit = 50             # 状态的输出维度
data_dim = 1              # 最终输出维度，即预测天数
timesteps = 3             # 时间步长

根据timesteps准备训练数据格式，series_to_supervised()函数按照timesteps提供输入的序列，然后划分能被batch整除的数据段，最后按照LSTM输入格式要求reshape张量。这里需要了解张量变换的重要性，相当于为了模型所需要的维度，去做相应的变换：

# 按batch拆分数据
reframed = series_to_supervised(scaled, timesteps, 1)
batch_len = len(reframed) // batch_size
batch_end = batch_len*8 // 10
train_scaled, test_scaled = reframed.values[0:batch_size*batch_end, :], reframed.values[batch_size*batch_end:batch_size*batch_len, :]
test_X, test_y = split_xy(test_scaled, timesteps, 1)
# 训练集中再分20%验证集
train_batch_len = len(train_scaled) // batch_size
train_batch_end = train_batch_len*8 // 10
train_scaled, val_scaled = train_scaled[0:batch_size*train_batch_end, :], train_scaled[batch_size*train_batch_end:batch_size*train_batch_len:, :]
train_X, train_y = split_xy(train_scaled, timesteps, 1)
val_X, val_y = split_xy(val_scaled, timesteps, 1)
# reshape
train_X_3D = train_X.reshape(train_X.shape[0], timesteps, data_dim)
val_X_3D = val_X.reshape(val_X.shape[0], timesteps, data_dim)
test_X_3D = test_X.reshape(test_X.shape[0], timesteps, data_dim)

开始准备模型，rnn_unit=50，stateful=True，一个LSTM层，一个dense层，这里试过加一个正则化dropout层，但效果没有提升，所以注释掉了，回调callbacks_list用于在验证集上调试，定义loss='mse'和优化器optimizer='rmsprop'：

model = Sequential()
model.add(LSTM(rnn_unit, stateful=True, batch_input_shape=(batch_size, timesteps, data_dim)))
# model.add(Dropout(0.2))
model.add(Dense(data_dim))
model.summary()
callbacks_list = [keras.callbacks.EarlyStopping(monitor='val_loss',patience=2,),
                  keras.callbacks.ModelCheckpoint(filepath='my_model.h5', monitor='val_loss',save_best_only=True,),
                  keras.callbacks.ReduceLROnPlateau(monitor='val_loss', factor = 0.01, patience = 2,)]
model.compile(loss='mse',               #mae
              optimizer='rmsprop')      #rmsprop，adam

keras层结构如下，模型不能设置过于复杂，总共需要训练50*(50+1+1)*4+(50+1)=10451个参数：

_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm_1 (LSTM)                (256, 50)                 10400     
_________________________________________________________________
dense_1 (Dense)              (256, 1)                  51        
=================================================================
Total params: 10,451
Trainable params: 10,451
Non-trainable params: 0
_________________________________________________________________

调优完超参后，在迭代epochs=150次过程中，在第126次后中止：

history = model.fit(train_X_3D, train_y, batch_size=batch_size, epochs=epochs, verbose=1,
              validation_data=(val_X_3D, val_y), shuffle=False, callbacks=callbacks_list)
# 绘画训练和测试数据集的损失曲线
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='validate')
plt.legend()
plt.show()
256/256 [==============================] - 0s 70us/step - loss: 0.0312 - val_loss: 0.0388
Epoch 125/150
256/256 [==============================] - 0s 143us/step - loss: 0.0312 - val_loss: 0.0388
Epoch 126/150
256/256 [==============================] - 0s 37us/step - loss: 0.0312 - val_loss: 0.0389

训练集和验证集损失图：

开始训练，喂入数据，循环epochs次，因为之前stateful=True，所以每次新的迭代需要用reset_states()重置LSTM状态变量：

for i in range(epochs):
    history = model.fit(train_X_3D, train_y, batch_size=batch_size, epochs=1, verbose=1,
              validation_data=(val_X_3D, val_y), shuffle=False, callbacks=callbacks_list)
    model.reset_states()

让我们看看训练的效果，150次迭代后，验证集上的loss值稳定在0.0379左右：

cost = model.evaluate(val_X_3D, val_y, batch_size=batch_size)
print('validate cost:', cost)
256/256 [==============================] - 0s 33us/step - loss: 0.0309 - val_loss: 0.0378
Train on 256 samples, validate on 256 samples
Epoch 1/1
256/256 [==============================] - 0s 31us/step - loss: 0.0309 - val_loss: 0.0376
Train on 256 samples, validate on 256 samples
Epoch 1/1
256/256 [==============================] - 0s 27us/step - loss: 0.0309 - val_loss: 0.0378
256/256 [==============================] - 0s 8us/step
validate cost: 0.03793208673596382

前面训练、验证、确定超参后，一旦运行测试集，就不能再根据运行结果作修改以防信息泄露。下面开始用这个model直接进行预测，按batch送入数据，按照之前数据处理顺序的逆过程，先还原标准化，再还原差分，最后还原对数：

# 预测
forecasts = list()
test_batch = batch_len - batch_end
for i in range(test_batch):
    test_batch_X, test_batch_y = test_X[i*batch_size:(i+1)*batch_size, :], test_y[i*batch_size:(i+1)*batch_size, :]
    predict_input = test_batch_X.reshape(batch_size, timesteps, data_dim)
    forecast = model.predict(predict_input, batch_size=batch_size)
    for j in range(len(forecast)):  
        forecasts.append(forecast[j,:])      # store the forecast
forecasts = np.array(forecasts)
# 定义还原为收入数值的函数
def diff_inverse(series, pred_data, scaler):
    inverted = list()
    for i in range(len(pred_data)):
        # create array from forecast
        forecast = array(pred_data[i])
        fc = forecast.reshape(len(forecast),1)
        # invert scaling
        inv_scale = scaler.inverse_transform(fc)
        # 当日预测差分数据 + 7天前的原始数据 = 当日预测收入
        if len(forecast) == 1:
            index = batch_end * batch_size + i + timesteps
            last_diff = series.values[index]
            inverted.append(inv_scale[0, :] + last_diff)
        else:
            for j in range(len(forecast)):
                index = batch_end*batch_size + i*batch_size + j + timesteps
                last_diff = series.values[index]
                inverted.append(inv_scale[j,:] + last_diff)
    return inverted
# 还原真实
real = diff_inverse(data, test_y, scaler)
# 还原预测
predicted = diff_inverse(data, forecasts, scaler)
predicted = np.array(predicted)
# 对数还原
real = np.exp(real)
predicted = np.exp(predicted)

计算测试集上的RMSE均方根误差，其值为36817.065：

# calculate RMSE
rmse = sqrt(mean_squared_error(real, predicted))
print('Test RMSE: %.3f' % rmse)
Test RMSE: 36817.065

保存文件，并绘制预测效果图：

# 保存预测结果
result = concat((DataFrame(real), DataFrame(predicted)), axis=1)
result = DataFrame(result)
result.columns = ['测试集收入真实值','测试集收入预测值']
# plt.plot(result)
# plt.show()
result.to_csv('output\\LSTM_predict_result.csv', encoding='utf_8_sig')
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure()
fig.add_subplot()
plt.plot(real, color='blue', label='真实值')
plt.plot(predicted, color='red', label='预测值')
plt.legend(loc='best')
plt.title('测试集预测效果比对')
plt.show()

图像如下，蓝色是真实值，红色是预测值，大部分情况拟合的很不错，部分拟合的不太好：

最后看数据，基本预测的都还不错，就是节日预测的很不好。我将测试集当日收入的真实值、指标值和预测值做了比对，预测数据比原先手工分解指标的效果要好：

最后，让我们看看模型的稳定性，连续运行几次：

validate cost: 0.037923164665699005
Test RMSE: 35885.605

validate cost: 0.03791944310069084
Test RMSE: 36851.139

毕竟这家门店的日收入标准差为49799，如果日均3万多元的误差在接受范围内，那么就 可以将这个模型的预测值作为日收入指标，即门店的次日收入期望 ，当然这个模型本身我认为还有进一步优化的余地。

四. LSTM模型预测（四）：增加特征维度 - 日期属性

既然模型拟合节日效果不好，我试图增加日期属性，程序没有太大变动，只是利用OneHot将日期属性进行编码，并作为输入特征：

# 特征“日期属性”离散化
data = pd.get_dummies(data,columns=['日期属性'])

OneHot编码效果如下图所示：

简单调参后，设置batch_size = 128、timesteps = 7、input_dim = 4，模型在50轮左右就中止了：

设置epochs = 50，训练速度很快，一两秒后得出结果：

128/512 [======>.......................] - ETA: 0s - loss: 0.0145
512/512 [==============================] - 0s 83us/step - loss: 0.0295 - val_loss: 0.0322
Train on 512 samples, validate on 128 samples
Epoch 1/1