什么是黎曼积分和勒贝格积分?两者区别是什么?
15 个回答
最近学习了一点勒贝格积分,在此记录一下理解。
蓝色:黎曼积分/类黎曼积分
红色:勒贝格积分

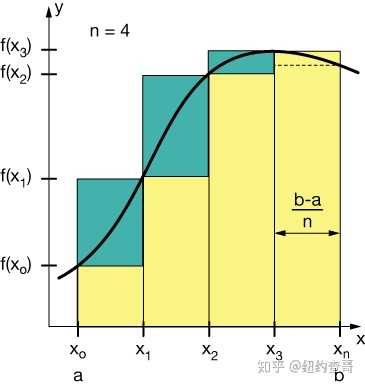
黎曼积分首先将一个函数的定义域分割成小区间,宽度为 \Delta x ,然后用这些区间的函数在这些区间上的值 f(x) 作为矩阵的高,然后将所有这些矩形的面积 f(x)·\Delta x 相加。这个积分是当矩形的宽度缩小到0时这个和的极限。
Lebesgue积分也是相似的,但是它涉及到切分一个函数的范围,而不是其域。可以说,勒贝格积分基本上是一个侧面的黎曼积分。
积分的直观含义是它给出了某个区域内函数的总量,它是求和的连续模拟。
Riemann和Lebesgue积分均以一定的极限值来计算曲线下的面积,该极限会填充越来越多的空间,最后求各极限面积做加和来作为积分的结果。
如果可以通过与该求和函数紧密匹配的矩形区域的限制,来找到该函数的积分部分,则该函数为Riemann可积。这是一系列接近它的阶跃函数,其中阶跃函数的每个部分都是该区间内某处函数的评估值,或区间最大值。
如果我们可以通过使用收敛到该求和函数的简单函数序列的极限,来找到函数的积分,则该函数是Lebesgue可积的。
此外,Riemann积分仅在变量间隔上定义,而Lebesgue积分在任何量度空间中定义,看起来定义的更宽泛一些,也就是说理论上如果 f(x) 是Riemann可积函数,则一定是Lebesgue 可积函数。
以上,谢谢⭐
分三个方面来讨论
一、就积分的定义而言:
详见文章: https:// zhuanlan.zhihu.com/p/64 278784
给一个直观的定义,严格的定义要从测度讲起,感兴趣可以参考文末的专栏链接。
Lebesgue 积分是用横切的 (基于函数值来分割定义域)阶梯来逼近 :

相比 Riemann 积分则是竖切的 (直接根据定义域里元素的值来分割积定义域) 来逼近:
还有一个图片中反映出来的细节:Lebesgue 积分是用小于等于函数值的一些列横切,然后求supremum来逼近 (也可以配合大于函数值的横切求infimum来夹逼);Riemann 积分会求一个上极限跟一个下极限,积分存在需要上极限跟下极限相等。
二、黎曼积分跟勒贝格积分的比较
详见文章: https:// zhuanlan.zhihu.com/p/65 130979
- 一个显而易见的优势是 Riemann 可积函数都是 Lebesgue 可积函数,所以 Lebesgue 积分可以看作是 Riemann 积分的拓展;但是注意 这个虽然很明显,却不重要 ,或者可以说不是 Lebesgue 积分的精髓所在——比如 Henstock-Kurzweil 积分在这方面可以做得更好
- Lebesgue 积分最重要的优势应该是它关于极限的性质,这些性质使得 Lebesgue 可积函数列逐点收敛的极限一般也是 Lebesgue 可积的 。所以很多 Lebesgue 可积函数相关的空间是完备的 (如 L^1 就是Banach Space/完备的)。而作为比较,Riemann 可积函数列逐点收敛的极限很多情况下是 Riemann 不可积的; 我们需要一致收敛的条件才能保证 Riemman 可积函数的极限可积 。一致收敛比起逐点收敛太强了,很难满足
- 再一个 Lebesgue 积分的优势就是它是基于测度来定义的,所以它能够被定义在更广义的空间上 (如概率空间)。而 Riemann 积分的定义需要一个"有序"的结构 (区间、区间上的分割等),这个使得它的实用性小很多,主要就是限制在了 \mathbb R^n 上
三、黎曼积分跟勒贝格积分的联系
Riemann 可积的函数都是 Legesgue 可测且可积的,且Riemann 积分存在的 充要条件 是被积函数不连续点构成的集合是一个 Lebesgue 零测集,而当这个条件满足时,Riemann 积分跟 Lebesgue 积分结果一致。
详细证明见文章: https:// zhuanlan.zhihu.com/p/65 517362
欢迎关注我的实分析专栏:




