整形数与浮点数转换及Verilog实现

前言

整形数与浮点数在计算机的硬件中以不同的形式存储。在之前的文章中介绍了浮点数的表示方法（ 单精度浮点数(float32)存储与表示方式 ），本文主要介绍整形数与浮点数的相互转换，以及基于Verilog语言的实现。

整形数转浮点数

如前文所述，IEEE 754标准规定一个单精度浮点数由 1 位符号位， 8 位指数部分和 23 位尾数部分组成。本文所提的整形均为 16 位。

无符号整形数转浮点数

考虑一个 16 位无符号整型数 uint 的表示方法：

uint=x_{15}x_{14}\dots x_1x_0, \quad x_i\in\{0,1\},i=0,1,2,\dots,15

不难得出，无符号整形数的范围为 0000\space0000_2\sim1111\space1111_2 \to 0_{\text{dec}}\sim65535_{\text{dec}} .

考虑单精度浮点数 float 的一般表示形式：

float=(-1)^{\text{sign}}\cdot2^{\text{Exponent}}\cdot1.\text{fraction}

注意到这里的 2^{\text{Exponent}} 和 1.\text{fraction} 为二进制表示，且对于无符号整型数来说，必然有 \text{sign}=1 .

由于 2^{\text{Exponent}} 与 1.\text{fraction} 相乘时，可以视为对 \text{fraction} 进行了 \text{Exponent} 次 移位 ，因此，拥有 23 位尾数部分的单精度浮点数通过移位，在 不缺失精度 的情况下，至多可以表示 24 位长的整数（ \text{fraction} 在小数点前还有一位有效数字 1 ）。对于所有 16 位长的整形数，浮点数可以完全地表示它们，而不缺失精度。

以下列出了几个整型数转浮点数的例子：

• 无符号0: 0000\space0000\space0000\space0000_2 \to 浮点0 \to 0\space(0000\space0000)\space(000\dots0000)_2
• 无符号1:0000\space0000\space0000\space0001_2 \to (-1)^{0}\cdot2^{127-127}\cdot1.0_2 \to 0\space(0111\space1111)\space(000\dots0000)_2
• 无符号2:0000\space0000\space0000\space0010_2 \to (-1)^{0}\cdot2^{128-127}\cdot1.0_2 \to 0\space(1000\space0000)\space(000\dots0000)_2 无符号65535:1111\space1111\space1111\space1111_2 \to 2^{142-127}\cdot1.111\space1111\space1111\space1111_2 \to 0\space(1000\space1110)\space(111\space 1111\space1111\space1111\space 0000\space0000)_2

注意到 \to 右侧的浮点数为IEEE 754标准表示法， 并用 () 将指数部分与尾数部分括了起来。

对于一个任意的无符号整形数 uint=x_{15}x_{14}\dots x_1x_0 ，在将其转换为浮点数时，可按以下几个步骤进行：

1. 首先可以确定，该整型数转换得到的浮点数符号位必定为 0 ；
2. 从最高位 (x_{15}) 开始向最低位 (x_0) 寻找第一个非 0 位，假设其为 x_a,\space a\in[0,15] , 则 x_a 确定了小数点的位置。该整形数可以表示为 2^{a}\cdot1.x_{a-1},x_{a-2},\dots,x_{0} 的形式，这样就确定了指数部分 \text{Exponent}=a , 尾数部分 \text{fraction}=x_{a-1}x_{a-2}\dots x_0 ；
3. 若不存在这样的非 0 位，则该无符号整型数为 0 ，则得到浮点数也为 0 ， 0 的阶码和尾数都为 0 .

有符号整型数转浮点数

有符号整型数相较无符号整型数多了一个符号位，一般为其最高位。考虑一个 16 位有符号整型数 int 的表示方法：

int=x_{15} x_{14}\dots x_1x_0, \quad x_i\in\{0,1\},i=0,1,2,\dots,15

将符号位记作 sign , 规定 sign=x_{15} . 不难得出，有符号整型数的范围为：

0\space000\space0000\space0000\space0000_2 \sim 0\space111\space1111\space1111\space1111_2\quad(sign=0)\\ 1\space000\space0000\space0000\space0000_2 \sim 1\space111\space1111\space1111\space1111_2\quad(sign=1)

在计算机内，带符号的数值，一般采用其 补码 进行存储，因其进行两数的加减计算比较方便。有关补码的概念，可见之前的文章 浮点数加减法介绍 。对于符号为正的数，其补码与原码形式相同，而对于符号为负的数，其补码为对其原码除符号位外，每位取反后，末位加1。以下是几个例子：

-1_{\text{dec}}\to1\space000\space0000\space0000\space0001(\text{Binary code})\to1\space111\space \space1111\space1111\space1111(\text{Implement code})

-2_{\text{dec}}\to1\space000\space0000\space0000\space0010(\text{Binary code})\to1\space111\space \space1111\space1111\space1110(\text{Implement code})

-32767_{\text{dec}}\to1\space111\space1111\space1111\space1111(\text{Binary code})\to1\space000\space \space0000\space0000\space0001(\text{Implement code})

特别地，对于 1\space000\space0000\space0000\space0000 , 对其计算补码后结果与原码相同。规定补码为 1\space000\space0000\space0000\space0000 的数为 -32768_{\text{dec}} . 因此， 16 位有符号数可以表示的十进制数的范围为 -32768\sim32767 .

对于有符号整型数转换为浮点数，需要将符号位也加入进行表示。考虑几个特殊的有符号整型数转浮点数的例子：

• 有符号0: 0\space000\space0000\space0000\space0000_2 \to 浮点0 \to 0\space(0000\space0000)\space(000\dots0000)_2
• +1: 0\space000\space0000\space0000\space0001_2 \to 0\space(0111\space1111)\space(000\dots0000)_2
• -1: 1\space000\space0000\space0000\space0001_2 \to (-1)^{1}\cdot2^{142-127}\cdot1.000\space0000\space0000\space0001_2 \to 1\space(1000\space1110)\space(000\space 0000\space0000\space0001\space0000\space0000)_2
• +32767: 0\space111\space1111\space1111\space1111_2 \to 0\space(1000\space1101)\space(111\space1111\space1111\space1110\space0000\space0000)_2
• -32767: 1\space111\space1111\space1111\space1111_2 \to (-1)^{1}\cdot 2^{141-127}\cdot1.111\space1111\space1111\space1110_2 \to 1\space(1000\space1101)\space(111\space1111\space1111\space1110\space0000\space0000)_2
• -32768: 1\space000\space0000\space0000\space0000_2 \to (-1)^{1}\cdot2^{142-127}\cdot1.000\space0000\space0000\space0000_2 \to 1\space(1000\space1110)\space(000\space0000\space0000\space0000\space0000\space0000)_2
• -16384: 1\space100\space0000\space0000\space0000_2 \to (-1)^{1}\cdot2^{141-127}\cdot1.000\space0000\space0000\space0000_2 \to 1\space(1000\space1101)\space(000\space0000\space0000\space0000\space0000\space0000)_2

对于一个任意的有符号整形数 int=x_{15} x_{14}\dots x_1x_0 ，在将其转换为浮点数时，可以按照以下几个步骤进行：

1. 根据整型数的符号位可以确定浮点数的符号位，即两者相等；
2. 从数值部分的最高位 (x_{14}) 开始向最低位 (x_0) 寻找第一个非 0 位，假设其为 x_a,\space a\in[0,14] , 则 x_a 确定了小数点的位置。该整形数可以表示为 -1^{sign}\cdot2^{a}\cdot1.x_{a-1},x_{a-2},\dots,x_{0} 的形式，这样就确定了指数部分 \text{Exponent}=a , 尾数部分 \text{fraction}=x_{a-1}x_{a-2}\dots x_0 ,
3. 若不存在这样的非零位，则根据符号位来判断该有符号整形数为 0 或 -32768 , 0 的尾数和阶码都为 0 , -32768 的尾数部分为 0 , 阶码为 142 .

浮点数转整型数

将浮点数转换成整型数时，需要考虑转换的溢出和舍入问题。

对于溢出，采用指数部分的低位来表示移位的次数。无符号整型数只考虑偏置后的指数部分的低 4 位，即偏置后的指数部分为 0\sim15 的情况。无符号整型数只考虑偏置后的指数部分为 0\sim14 的情况，指数部分为 15 时，若尾数部分为全 0 且符号位为 1 ，则应视为 -32768 .

对于舍入，即尾数部分的低位在转换中进行舍弃。无符号整形数在指数偏置不同的情况下用到的尾数的位数如下所示：

\begin{aligned} \text{Exponent} &= 15\to uint= 1\space fraction[22:8]\\ \text{Exponent}&=14\to uint= 01\space fraction[22:9]\\ &\dots\dots\\ \text{Exponent}&=1\to uint=0000\space0000\space0000\space000\space fraction[22]\\ \text{Exponent}&=0\to uint=0000\space0000\space0000\space0001 \end{aligned}

其余尾数均被舍弃。特别地，当指数部分的偏置为负时，转换后的数应为 0 .

有符号整型数在偏置不同的情况下指数偏置不同的情况下用到的尾数的位数与无符号整形数类似，但它在指数偏置为 15 时应该特殊考虑，即

\begin{aligned} \text{Exponent} = 15\to int&= 1\space 000\space0000\space0000\space0000 \\ \text{Exponent}=14\to int&= sign\space 1\space fraction[22:9]\\ &\dots\dots\\ \text{Exponent}=1\to int&=sign\space 000\space0000\space0000\space000\space fraction[22]\\ \text{Exponent}=0\to int&=sign\space 000\space0000\space0000\space0001 \end{aligned}

其余尾数均被舍弃。特别地，当指数部分的偏置为负时，转换后的数应为 0 .

Verilog仿真模拟

使用Verilog硬件描述语言进行整形数转浮点和浮点转整形数的实现，并使用VIVADO进行仿真。仿真结果如下所示。

从上往下波形分别为：

• uint16_in[15:0]： 16 位无符号整形数输入，范围为 0\sim65535 ;
• float1_out[31:0]：由uint16_in转换得到的 32 位浮点数输出；
• uint16_out[15:0]：由float1_out转换得到的 16 位无符号整型数输出；
• uint16_float_int16_out[15:0]：由float1_out转换得到的 16 位有符号整型数输出；
• expo_nonbias[7:0]：float1_out除去偏置后的指数部分值；
• int16_in[15:0]： 16 位有符号整型数输入，范围为 -32768\sim32767 ；
• float2_out[31:0]：由uint16_in转换得到的 32 位浮点数输出；
• int16_out[15:0]：由float2_out转换得到的 16 位有符号整型数输出；
• int16_float_uint16_out[15:0]：由float2_out转换得到的 16 位无整形数输出；
• expo_nonbias[7:0]：float2_out除去偏置后的指数部分值。

以下是几个特殊情况：

输入无符号uint16_in为 1 , 转换后的无符号uint16_out输出结果与输入相同，转换后的有符号uint16_float_int16_out的结果为 1 ；

输入有符号int16_in为 -32767 ，转换后的有符号int16_out输出结果与输入相同，转换后的无符号int16_float_uint16_out的结果为 32769 .

输入无符号uint16_in为 32767 , 转换后的无符号uint16_out输出结果与输入相同，转换后的有符号uint16_float_int16_out的结果为 32767 ；

输入有符号int16_in为 -1 , 转换后的有符号int16_out输出结果与输入相同，转换后的无符号int16_float_uint16_out的结果为 65535 .

输入无符号uint16_in为 32768 , 转换后的无符号uint16_out输出结果与输入相同，转换后的有符号uint16_float_int16_out的结果为 -32678 ；

输入有符号int16_in为 0 , 转换后的有符号int16_out输出结果与输入相同，转换后的无符号int16_float_uint16_out的结果为 0 .

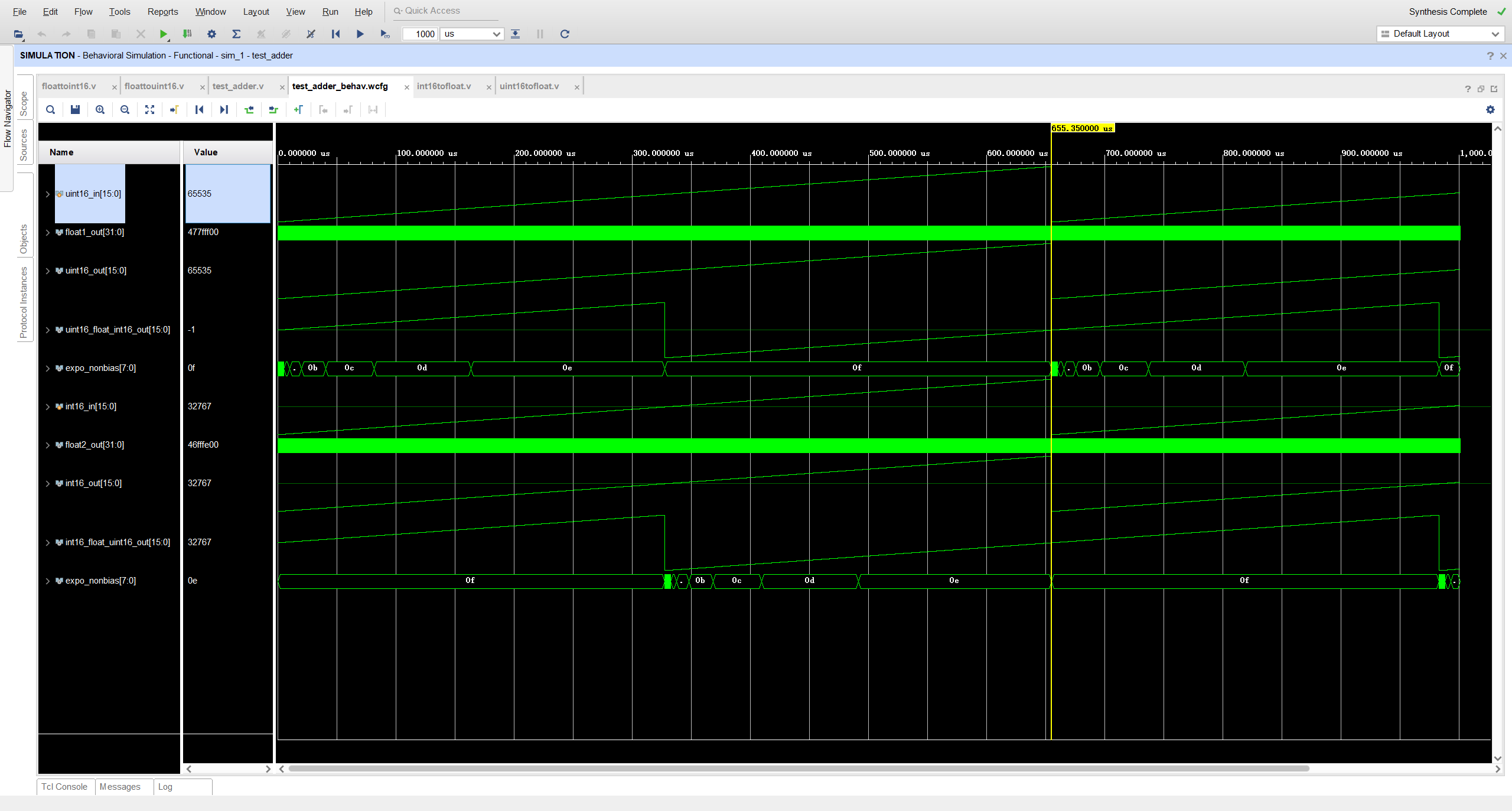
输入无符号uint16_in为 65535 , 转换后的无符号uint16_out输出结果与输入相同，转换后的有符号uint16_float_int16_out的结果为 -1 ；

输入有符号int16_in为 32767 , 转换后的有符号int16_out输出结果与输入相同，转换后的无符号int16_float_uint16_out的结果为 32767 .

后记

本文简要介绍了整型数与浮点数互相转换的方法，并介绍了其Verilog实现思想。仿真部分的验证仅针对 16 位无符号整型数和有符号整型数进行了验证。若有错误，欢迎指出。