热力学第二定律（二）-熵与克劳修斯不等式

在已经了解卡诺循环的基础之上，我们来看一个任意循环过程。

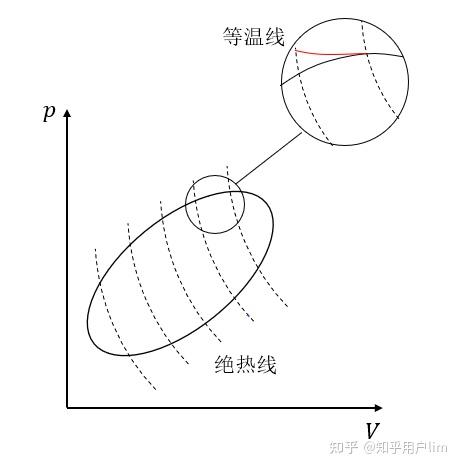
任意给定一个循环过程，我们可以用许多绝热线将其分割，再用等温线对其进行近似，最后可以将其划分为许多个小的卡诺循环之和。 其具体的证明需要用到更为复杂的数学知识。

根据我们对卡诺循环的理解，任给一个卡诺循环，其热温商的总和是0，因此该总循环的热温商之和可以写作下式：

\sum{\frac{\delta Q}{T}}=\frac{\delta Q_1}{T_1}+\frac{\delta Q_2}{T_2}+…+\frac{\delta Q_n}{T_n}=0

注意到过程可逆，此时系统的温度也是环境的温度。对此式稍作整理有：

\oint\frac{\delta Q}{T}=0

因此我们知道，系统的热温商在经历一个环路积分之后为0。 根据高等函数的积分定理，沿封闭曲线的环路积分为零，说明被积变量是某个函数的全微分。 该变量的积分值只取决于积分的起始和终末位置且与具体的途径无关，也就是说该函数是一个状态函数。

定义：

dS\equiv\frac{\delta Q_r}{T}

对微分式进行积分得到积分表达式：

\Delta S=\int^2_1\frac{\delta Q_r}{T}=\frac{Q_r}{T}

然后我们用类似的方法导出克劳修斯不等式。在上面的内容当中我们先证明了微小可逆循环的热温商变化之和为零，再利用环路积分的性质导出了熵的定义；接下来我们会讨论与之对应的微小不可逆过程的情况。

考虑之前导出的一个定理：任意两个热源之间工作的热机，总是卡诺热机的效率最大。不妨假设一个不可逆热机 ir 与可逆热机 r ，假设二者均从高温热源处取出相同多的热量。二者之间的效率总是有如下关系：

\frac{T_h-T_c}{T_h}>\frac{Q_h+Q_c}{Q_h}

上式左端即理论效率极限，也就是可逆热机的效率；右式代表实际效率，也就是非可逆热机的效率。其次，不等式右边的分子上，注意 Q_c 是系统与低温热源间交换的热量，由于系统总是向低温热源放热，尽管代数式中二者是相加，但实际上 Q_c 的值小于零。

因为卡诺机从高温热源处取出了热量，记作 Q_r 。并将任意热机对低温热源所放出的热记作 Q_{ir} 。据此我们对上式进行恒等变形。（ 注意将这里与第一节对应理解）

\frac{Q_{ir}}{T_c}+\frac{Q_r}{T_h}<0

此式表明， 对于任意微小不可逆过程 ，其热温商变化之和一定小于0。任意给定一个循环，我们也可以用之前类似的办法得到类似的结论。对于不可逆过程，其总的热温商变化之和一定小于0：

\sum\frac{\delta Q}{T}<0

改写成积分的形式：

\oint\frac{\delta Q}{T}<0

结合可逆过程的情况。对于某过程热温商的环路积分，如果结果小于0，则该过程不可逆；如果结果为0，则该过程可逆，数学表达式即：

\oint\frac{\delta Q}{T}\leq0 _{可逆}^{不可逆} 可逆时等号成立

现在再将我们刚才考虑的两个热机其中的卡诺热机扭转工作方向，从而得到一个循环过程，利用上面环路积分的性质，我们来分析一下这个过程。

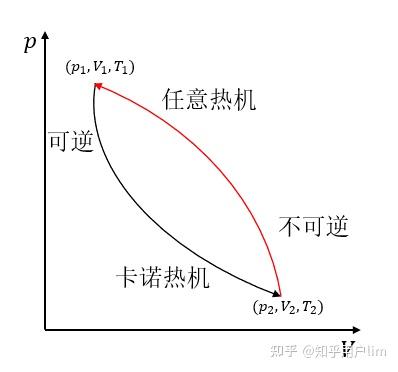
该循环的一个方向可逆，另一个方向不可逆，总的来看该循环不可逆。根据上面的式子：

\oint\frac{\delta Q}{T}<0

拆分为两个方向的积分：

\int^f_i\frac{\delta Q_r}{T}+\int^i_f\frac{\delta Q_{ir}}{T}<0

考虑可逆过程进行时无法区分方向，因此不等式的左边第一项可以通过改写得到下式：

-\int^i_f\frac{\delta Q_r}{T}+\int^i_f\frac{\delta Q_{ir}}{T}<0

移项得到：

\int^i_f\frac{\delta Q_r}{T}>\int ^i_f\frac{\delta Q_{ir}}{T}

结合熵的定义即：

\Delta^i_fS>\int_f^i\frac{\delta Q_{ir}}{T}

考虑到状态函数的性质，抑或是重新定义反应的方向，也可以得到下式：

\Delta^f_iS>\int_i^f\frac{\delta Q_{ir}}{T}

同时得到该式的微分形式：

dS>\frac{\delta Q_{ir}}{T}

不难看出，当该式取等时，循环可逆。 值得注意的是，该式中的T表示环境温度，可以记作，只有在可逆的时候才等于。 如果将取等的条件加入至上式：

dS\geq\frac{\delta Q}{T}^{不可逆}_{可逆}

此式即克劳修斯不等式。克劳修斯不等式也是热力学第二定律的数学表达式。

后续已更新

您的赞同、喜爱、收藏和转发能让更多的人看到这篇文章，这对我是极大的鼓励！

如果您感到满意，请双击屏幕点个赞再走吧！