决定系数R2能否为负数?
本文翻译自以下文章
R2 —— 评估回归的方法
回归是将函数拟合到数据的方法。例如,我们能够通过卫星统计沃尔玛门口停车场的汽车数量,也可以通过其收益报告了解沃尔玛在对应时段的销售额。于是,你想建立一个汽车数量与沃尔玛季度收益的函数关系,以便于您炒股。但是,在建立了汽车数量与季度收益的函数关系以后,我们应该如何评判你和出来的函数关系的优劣呢?常用的度量拟合效果的参数是决定系数R2。本文将详细介绍R2的计算原理及负值产生的原因分析:
什么是R2?
R2用于比较回归模型的预测误差与简单的Y=样本点平均值的误差。
R2的公式如下:
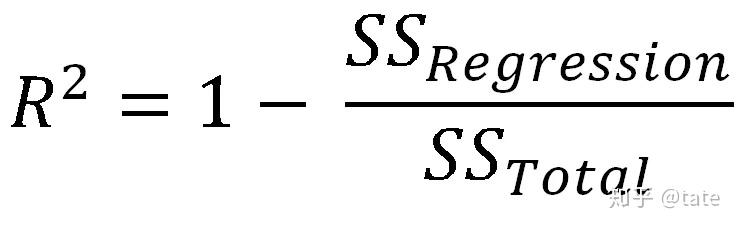
SS_Regression表示的是函数拟合得到的回归模型的预测值与真实值的误差的平方和

可以看下面这张图片,这里的黑色曲线就是通过数据拟合出来的一条回归曲线,上面计算的SS_Regression就是蓝色线(真实值)与黑色线(回归预测值)之间的误差。

SS_Total是表示Y=所有样本点平均值这么一条水平线与真实值之间误差的平方和。

我们计算出来了回归曲线的误差以后,跟谁去比较呢?这里选择了Y=所有样本点平均值这么一条水平线。计算真实值(蓝色线)和Y=所有样本点平均值这条直线的误差平方和。

通过上面的分析,我们可以得到以下结论:
- 决定系数R2是回归函数与Y=平均值这条水平线误差的比较;
- 只要样本点固定,SSTotal是固定不变的,回归函数或模型误差越小则SS_Regression这一项越小,R2就越趋近于1。
回归到最开始的问题,什么时候R2为负数?
R2为负数就是你得到的拟合函数预测误差大于Y=平均值这条函数的预测误差。
但是,这不是在侮辱人吗?
辛辛苦苦设置参数调整模型得到的拟合结果误差还比盲猜一个平均值大,这样的腊鸡模型咱也不敢放到台面上来。所以在市面上咱们很少见到R2小于零的模型。
所以一般认为有用的模型的R2的取值范围在0-1之间。
结论 回归函数拟合效果差于取平均值时R2会为负数

