深度势能学习(1)—基本知识
毕设做的是深度势能(Deep-Potential),对自己是全新的尝试,在课题组里算是第一个吃螃蟹的人。开始挺头秃的,从安装开始,到软件如何能跑起来,构型如何采样,训练的势函数怎么验证,机器文件如何配置,遇到过各种各样的问题,自己一次又一次碰壁。但好在遇到了很多善良的老师,对自己的问题都耐心解答。自己也借此记录自己学习过程中的一些认识,目前还比较粗浅,也存在不少错误,有问题的望批评指正。
1. 基本认识
势能面(PES) 是用于描述化学体系的一个基本量,由势能面可以得到大量的原子间相互作用信息。传统的 MD模拟 采用的是基于物理经验得到的解析函数来描述PES,即所谓的经验力场,虽然在一定程度能够描述体系原子在较长的时间尺度下的相互作用,但是人为定义的函数形式无法完整描述原子间复杂的多体相互作用。 第一性原理计算(First-Principles) 基于薛定谔方程进行电子自洽计算,没有经验参数的引入,对小体系问题能够准确描述。但是由于计算成本高,且受限于计算硬件的发展,只能处理一些较小的体系以及较小的时间尺度。
机器学习(ML) 方法的兴起被应用于构建势函数,而在众多的机器学习方法中, 人工神经网络 拟合势函数受到了广泛的关注。前馈神经网络用于拟合势能面最早是由Blank在1995年提出,用于研究CO在Ni表面以及H2在Si表面的扩散问题。虽然之后有大量的相关研究报道,但是人们也发现了问题:前馈神经网络只能受限于低维体系。原因是:
(1)缺少合适的输入坐标使体系能量满足平移、旋转和置换对称性;
(2)NN的输入节点不能改变,只能适用于固定体系大小;
(3)输入节点的数量与体系的自由度有关,因而不能扩展到高维体系,否则NN大小过大难以处理。
2. 高维神经网络势函数
在2007年由 Behler 和 Parrinello 提出了适用于高维体系的 高维神经网络势函数(NNPs) 。
高维神经网络势函数是一种 原子势 。原子势是基于体系每个原子的局域化学环境来拟合体系的相关性质,即每个原子采用一个单独的前馈神经网络表示。在高维神经网络势中,原子化学环境是用 中心原子框架的对称函数(ACSFs) 来描述,这些对称函数构成了原子化学环境的 描述符 (Descriptor)。描述符需要满足旋转、平移以及置换对称性。
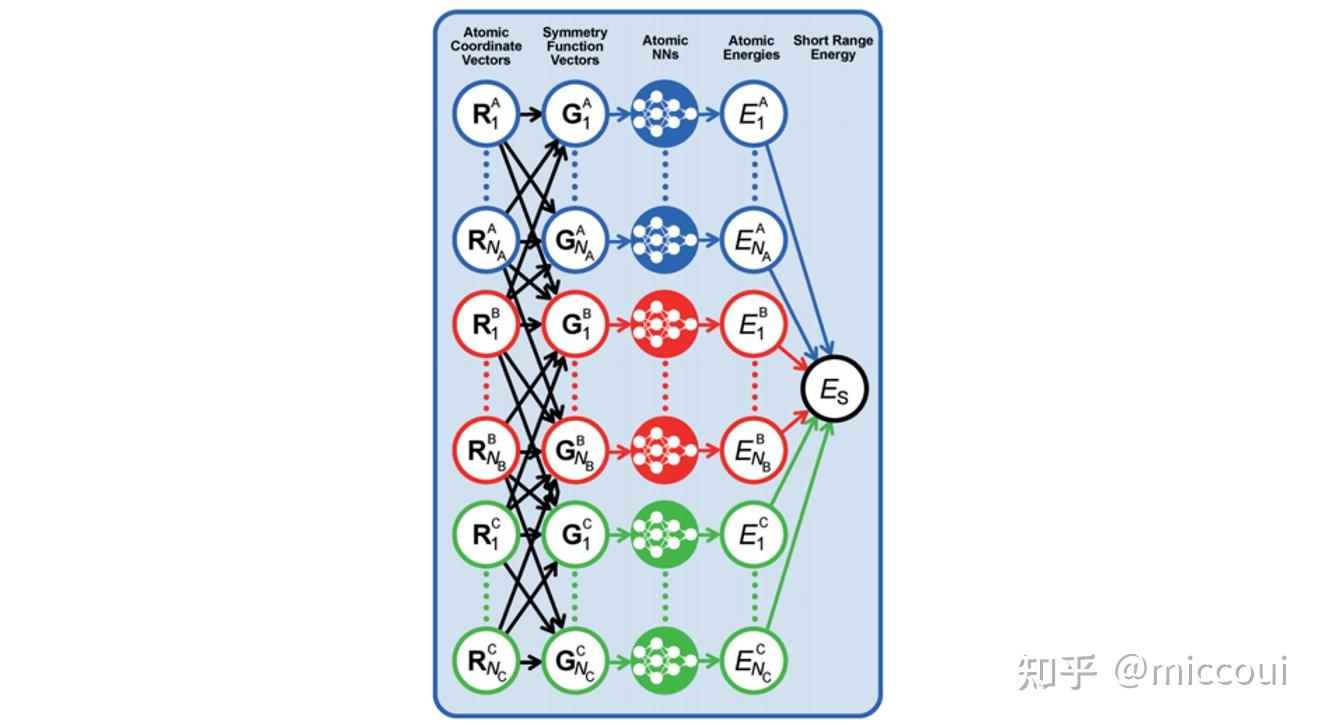
在 Behler 他们的工作中提出用多个不同超参数的径向分布函数和角分布函数来构建体系的描述符的:
(1)径向分布函数
G_i^1=\sum_j e^{-\eta(R_{ij}-R_c)^2}\cdot f_c(R_{ij})\\ f_c(R_{ij})=\begin{cases} 0.5\cdot\begin{bmatrix} cos(\frac{\pi R_{ij}}{R_c})+1 \end{bmatrix}\quad for \quad R_{ij}< R_c \\ 0 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad for \quad R_{ij} >R_c \end{cases}\\
(2)角分布函数
G_i^2= 2^{1-\xi}\sum_j\sum_{k\neq j}(1+\lambda \cdot cos(\theta_{ijk}))\cdot f_c(R_{ij})f_c(R_{ik})f_c(R_{jk})\\
NNPs 的基本思想是采用对称函数矢量描述不同元素、不同原子的邻域环境,然后采用原子神经网络预测不同原子对体系全局性质的贡献。即:
E_S=\sum_{\nu=1}^{N_{elem}}\sum_{\mu=1}^{N_{atoms,\nu}}E_{\mu}^{\nu}\\ 则原子受力可用下式计算:
F_{\alpha_i} = -\frac{\partial E_S}{\partial \alpha_i}=-\sum_{\mu =1}^{N_{atoms}}\frac{\partial E_{\mu}}{\partial \alpha_i}=-\sum_{\mu=1}^{N_{atoms}}\sum_{\nu=1}^{N_{G,\mu}} \frac{\partial E_{\mu}}{\partial G_{\mu,\nu}}\cdot\frac{\partial G_{\mu,\nu}}{\partial \alpha_i}\\
3. 采样策略
对于简单的体系,利用神经网络拟合得到的势函数能够较为准确地描述体系的能量。而对于复杂体系,少量的第一性原理计算得到的训练数据集仅能保证训练得到的势函数在于训练集接近的构型预测上表现良好,而对描述不完备的区域的预测效果会产生较大的误差,因此对采样策略提出了要求。
为了保证NNPs势能模型的可靠性,就需要训练数据能有效覆盖样本空间,即保证 充足采样 ;同时由于第一性原理计算量大,如何选取训练价值高的构型进行DFT计算也是研究者需要考虑的问题,即实现 样本筛选 。
不同研究者提出了许多采样策略,其中目前被广泛认可的是基于 同步学习 的采样方案,也是DP团队在DP-GEN采样器中使用的方法,后面讲DP-GEN时会提及。
4. 参考文献
[1] Jorg, Behler. First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems.[J]. Angewandte Chemie (International ed. in English), 2017. [2] Blank T B , Brown S D , Calhoun A W , et al. Neural network models of potential energy surfaces[J]. Journal of Chemical Theory & Computation, 1995, 103(10):4129-4137. [3] Behler J , Parrinello M . Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces[J]. Physical Review Letters, 2007, 98(14):146401. [4] Zhang Y , Wang H , Chen W , et al. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models[J]. 2019.
