透射电镜数据处理系列-1:TEM电子衍射花样标定
零度君经常做TEM,因而不少同窗会找我来折腾TEM的数据。虽然说每次折腾完最少也能收获一杯奶茶作为报酬......但是时间真是伤不起呀。所以我干脆开贴写一个系列的简单教程吧......
通常而言,最常见的问题是标定电子衍射花样......所以第一期我们讲一下衍射花样的标定。
先说好,我们前半部分只说步骤,后半部分说一下常见的问题和处理方法。不提太深入的理论......不然这不知道要从什么地方开始了......
衍射标定的步骤和基本原理
倒易矢量和面间距
电子衍射花样的标定实际上就是 通过电子衍射花样测量样品中晶面的间距和晶面法向的夹角 ,对照标准图谱来确定样品的晶体结构。
而这个测量,具体来说就是通过测量倒易点阵来完成的(衍射点花样是倒易点阵的一部分)。基本运算规则是这样的:
(hkl)晶面的倒易矢量:
\vec{g}_{hkl}=h\vec{a}^*+k\vec{b}^*+l\vec{c}^* \tag1
其中a*, b*, c*分别是倒易点阵的基矢,倒易点阵我们就不细讲了。我们要用的是下面这个公式:
\left| \vec{g}_{hkl} \right|=\frac{1}{d_{hkl}} \tag2
其中 d_{hkl} 是(hkl)晶面的面间距。
那么,从衍射普中是怎么测出倒易矢量 \vec{g}_{hkl} 的呢?其实就是从透射斑指向对应的衍射斑的矢量。
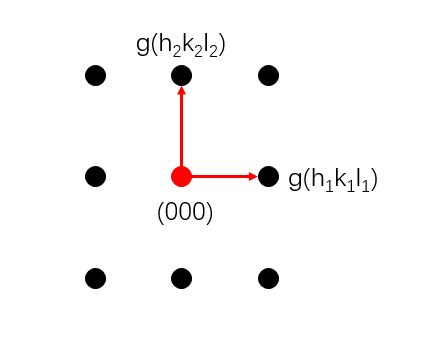
上图中红色箭头的长度就是 \left| \vec{g}_{hkl} \right| 单位是 nm^{-1} ,简单的取倒数就是晶面间距了。至于如何从图像中的长度换算成 nm^{-1} 为单位的倒空间长度,我们放在后面。
倒易矢量和晶面夹角
距离说完了我们该说夹角了。夹角是最简单的了,如上图中 \vec{g}_{h_1k_1l_1} 与 \vec{g}_{h_2k_2l_2} 的夹角就是晶面 (h_1k_1l_1) 与 (h_2k_2l_2) 。具体原因看倒易点阵推导就能明白,倒易矢量和晶面就是垂直的。因此夹角:
\cos\theta=\frac{\vec{g}_{h_1k_1l_1}\cdot \vec{g}_{h_2k_2l_2}}{|\vec{g}_{h_1k_1l_1}||\vec{g}_{h_1k_1l_1}|} \tag3
前面我们也说了知道了夹角与晶面间距后和数据库对比就能知道到底是什么结构了。
说完了基本原理,那么具体怎么操作呢?其实找零度君来问的同学一般都是卡在两个问题上:
- 怎么从图像中测出倒易矢量
- 从哪里搞来标准图谱的数据
从衍射图像测量倒易矢量的方法
从DM软件中直接读取
这是最简单也是最常用的方法,如果你获得的衍射数据是dm3文件的话(当然理论上dm4也一样,不过要换个高版本的软件)使用DigitalMicrograph(这软件网上一大把)打开直接测量就可以。
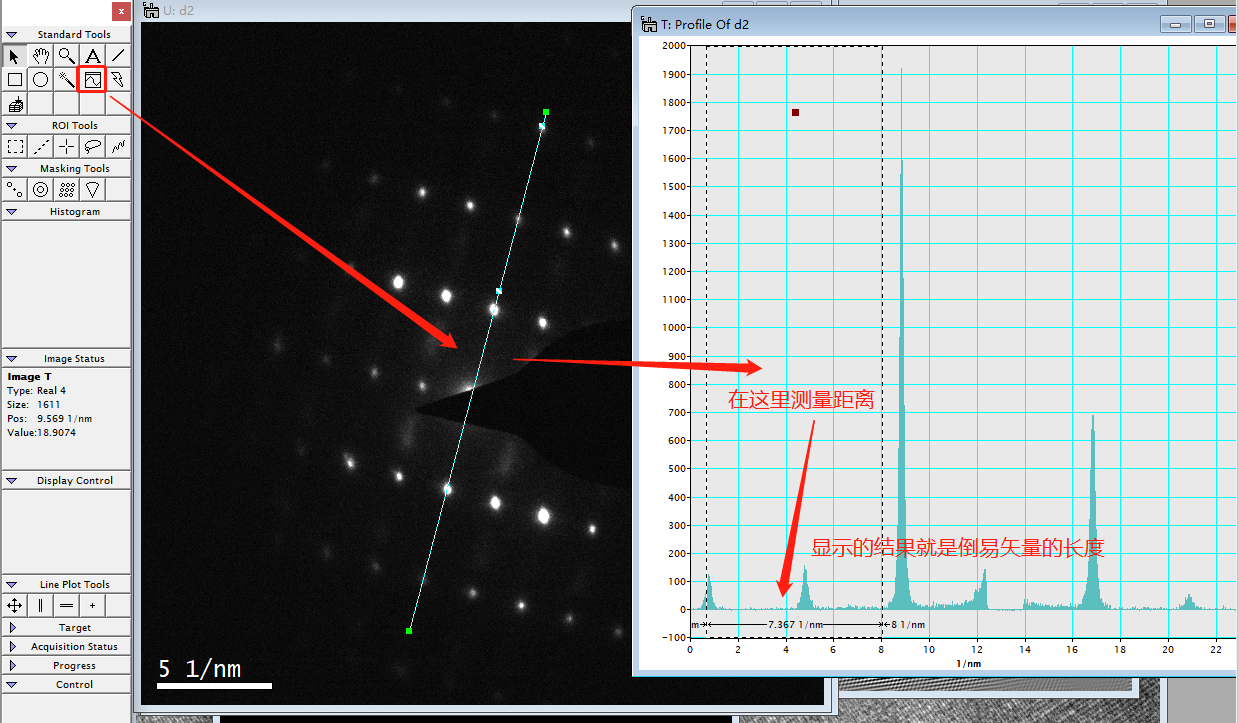
然后对倒易矢量的模取倒数就可以知道晶面间距了......是不是非常简单呀
长度非常好测量,那么角度呢?实际上DM是自带了测量角度的功能的,但是是付费功能(当然你可以找破解版......)那么不破解要怎么测量呢?
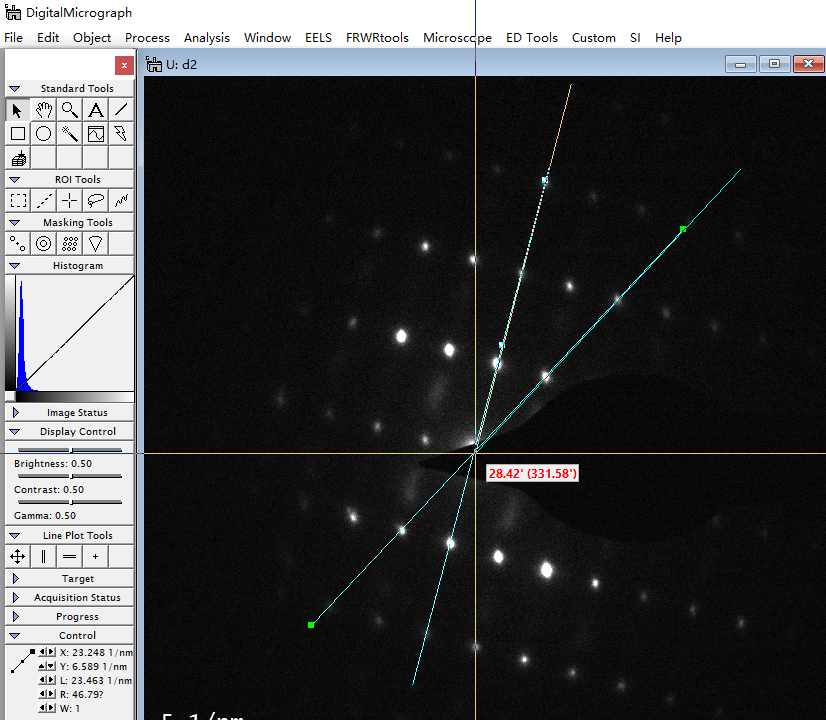
实际上我们用鼠标选中刚刚测量用的那条直线,点开Control面板,里面有个R就是当前直线的倾斜程度(单位角度)。分别测量两条直线的倾斜程度,做差就知道角度了。
下面这条的的R是75.21度
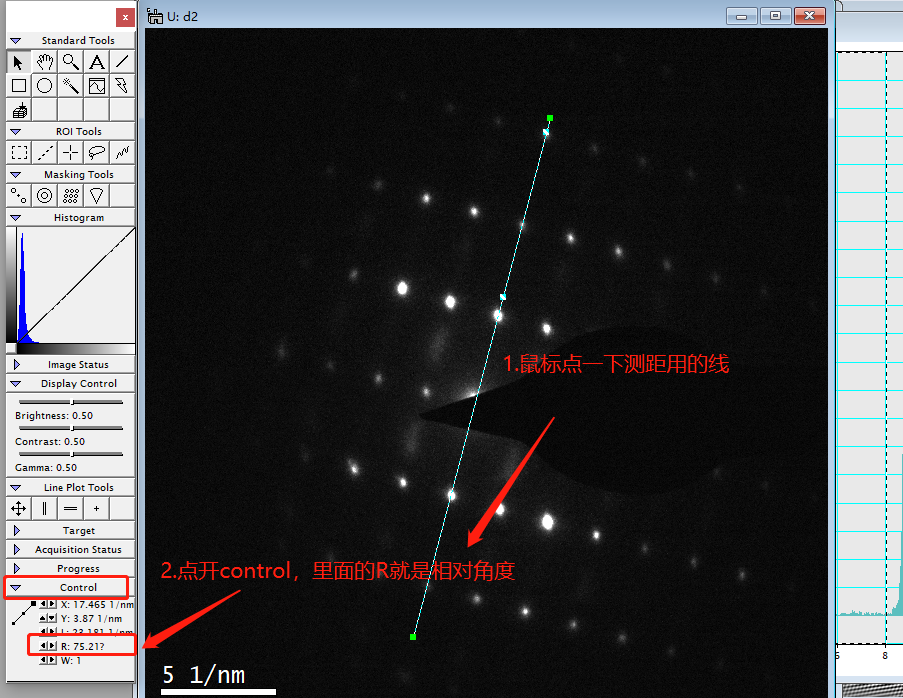
第二条的R是46.79度
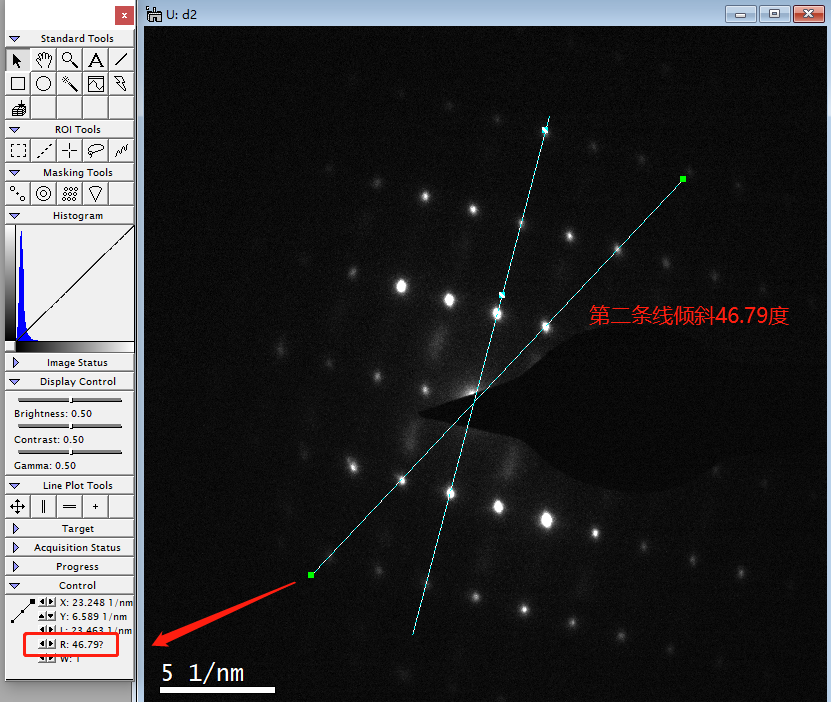
那么夹角就是75.21-46.79=28.42度,实际上标定的时候一般角度偏差1~2度都是正常现象。
如果你还觉得麻烦,那么我这里还有一个方法:就是用屏幕量角器,比如这个:
(个人用户免费)
启动量角器
测量结果28.42度,完美
参照物矫正标尺
如果你得到的结果是Tiff格式或者其他图片格式的,但是带有一个标尺。那么只需要先根据已知标尺对图像进行校正就可以用DM处理了。
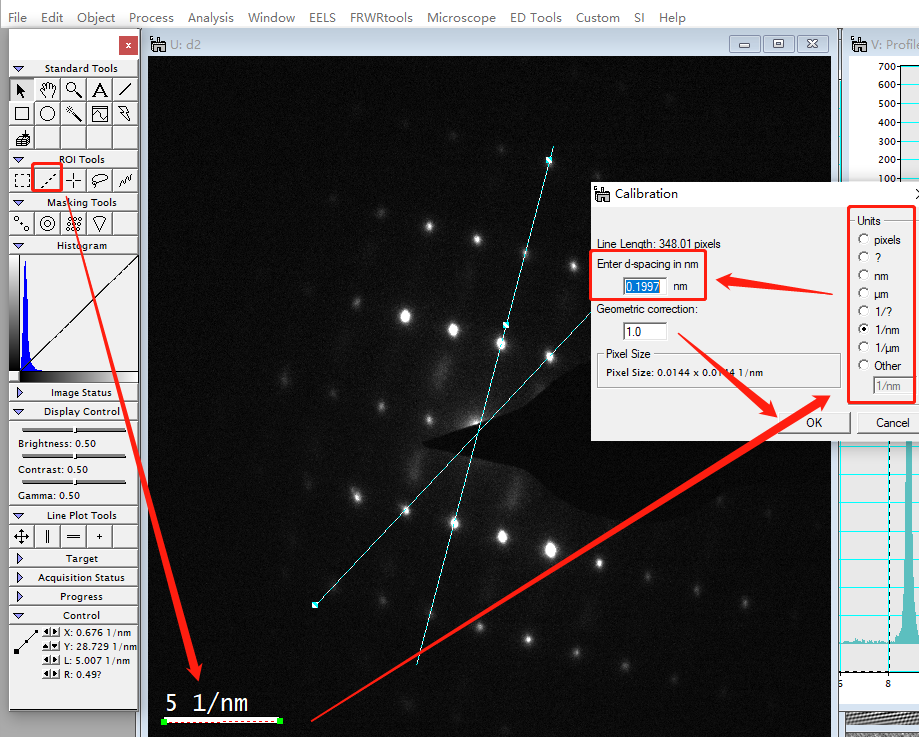
方法是先在ROI工具中拉一条已知长度的线(一般就是标尺),然后点开Analysis中的Calibration选项卡,输入已知长度。需要注意的是!!!如果你的长度单位是1/nm或者1/μm等倒空间长度单位,那么要换算成正空间输入!!!
比如已知虚线长度是2 (1/nm)那么你应该输入0.5nm
胶片法
在一些年龄较大的电镜上,我们需要用胶片来记录衍射信息,零度君也碰上过好多次了。胶片虽然让衍射标定变得很麻烦但是胶片可以获得非常强的曝光,这点是很多CCD都比不上的。胶片大致长这样:

注意下面的信息,通常会包含设备、胶片号、相机常数和加速电压。上图中25cm就是相机常数,200.0kV就是加速电压。计算方式是:
Rd=\lambda L \tag4
其中R就是胶片上衍射斑的距离,d是晶面间距,L是相机常数, \lambda 是电子波长。如果你用扫描仪扫描了底片,那么一定要注意扫描仪的放大倍数,你一定要把R换算成实际胶片上的长度才行。
电子波长可以根据加速电压计算出来,当然必须要考虑相对论效应(否则电子会超光速滴),记不得怎么换算的话就联立下面的方程即可:
\cases{ E_k=mc^2-m_0c^2\\ m=\gamma m_0\\ \gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\\ p=\gamma mv \\ \lambda=\frac{h}{p} } \tag5
其中Ek表示电子动能,对应加速电压给予的能量,m0是电子静质量,p是动量,h是普朗克常数。对于常用的几个电压,数据如下:
- 80kV:4.18pm
- 120kV:3.35pm
- 200kV:2.51pm
- 300kV:1.97pm
- 500kV:1.42pm
- 1000kV:0.872pm
- 1250kV:0.736pm
然后按部就班的算一个点,导入DM里校正标尺就行了......到此,怎么获取倒易矢量的长度的角度基本就讲完了。下面我们该说怎么获得标准图谱了
获得标准图谱数据的方法
晶体学数据库+JEMs
最简单的方法就是用晶体学数据库(比如ICSD等)找cif文件然后导入到JEMs软件中直接计算标准图谱。打开JEMS导入cif文件
然后点击Drawing-Diffraction

就可以看到不同带轴的衍射花样了。点击衍射点可以查看具体的信息,比如倒易矢量的长度。
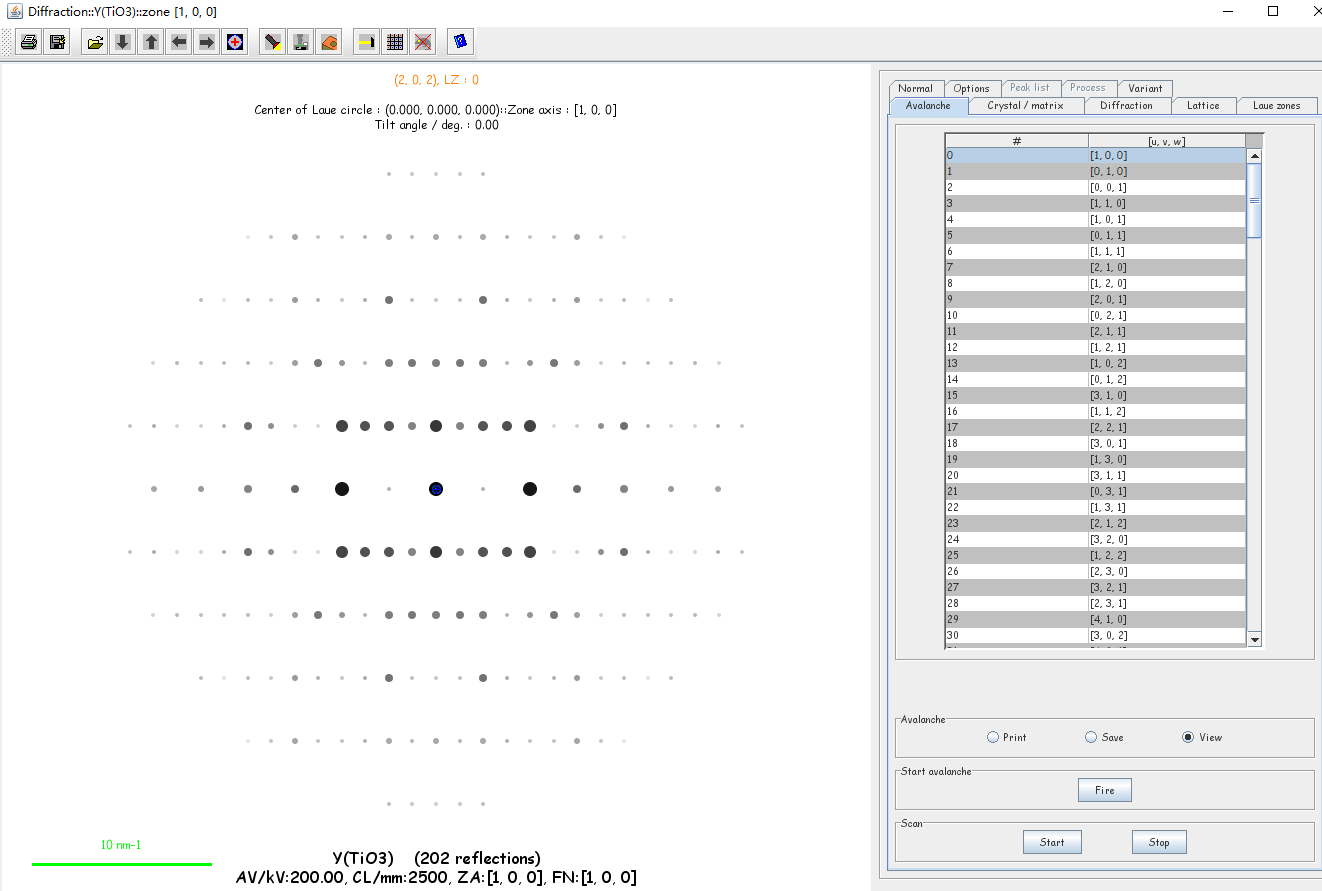
当然你也可以使用Material Studio等软件手动构建晶体模型
PDF卡片
除了直接使用晶体学数据库外,你还可以使用jade或者Findit等软件检索PDF卡,比如网上广为流传的PDF2004数据库。

在PDF卡中可以检索到物相的d(注意单位是A),取倒数就是衍射斑的距离g了。不过缺点也是有的......这玩意没法自动计算角度......所以角度需要看下面的方法手算......
手动计算
实际上只需要知道晶格常数,我们就可以计算晶面间距和夹角,方法如下:
\frac{1}{d_{hkl}^2}=\frac{\frac{h}{a}\left| \begin{array}{} h/a & \cos\gamma & \cos\beta\\ k/b & 1 & \cos\alpha\\ l/c & \cos\alpha & 1 \end{array} \right| +\frac{k}{b}\left| \begin{array}{} 1 & h/a & \cos\beta\\ \cos\gamma & k/b & \cos\alpha\\ \cos\alpha & l/c & 1 \end{array} \right| +\frac{l}{c}\left| \begin{array}{} 1 & \cos\gamma & h/a\\ \cos\gamma & 1 & k/b\\ \cos\beta & \cos\alpha & l/c \end{array} \right|} { \left| \begin{array}{} 1 & \cos\gamma &\cos\beta\\ \cos\gamma & 1 & \cos\alpha\\ \cos\beta & \cos\alpha & 1 \end{array} \right| } \tag6
其中abcαβγ是晶格常数
同样的夹角:
\cos\theta=\frac{\vec{g}_{h_1k_1l_1}\cdot \vec{g}_{h_2k_2l_2}}{|\vec{g}_{h_1k_1l_1}||\vec{g}_{h_1k_1l_1}|} =\frac{(h_1\vec{a}^*+k_1\vec{b}^*+l_1\vec{c}^*)\cdot(h_2\vec{a}^*+k_2\vec{b}^*+l_2\vec{c}^*)} {|h_1\vec{a}^*+k_1\vec{b}^*+l_1\vec{c}^*)||h_2\vec{a}^*+k_2\vec{b}^*+l_2\vec{c}^*|} \tag7
看上去可能有点复杂......不过对于一些对称度高的晶体,可以很大的简化,比如对于正交结构(当然,立方和四方也可以用):
\cases{ \frac{1}{d_{hkl}^2}=\frac{h^2}{a^2}+\frac{k^2}{b^2}+\frac{l^2}{c^2}\\ \cos\theta=\frac{h_1h_2/a^2+k_1k_2/b^2+l_1l_2/c^2} {(h_1^2/a^2+k_1^2/b^2+l_1^2/c^2)^{(1/2)}(h_2^2/a^2+k_2^2/b^2+l_2^2/c^2)^{(1/2)}} }\tag8
对于立方结构就非常简单了:
\cases{ \frac{1}{d_{hkl}^2}=\frac{h^2+k^2+l^2}{a^2}\\ \cos\theta=\frac{h_1h_2+k_1k_2+l_1l_2}{\sqrt{h_1^2+k_1^2+l_1^2}\sqrt{h_2^2+k_2^2+l_2^2}} } \tag9
更多公式可以参阅任何一本材料科学基础或者晶体学教程......但不建议手动计算立方、四方和正交之外的晶体......这种复杂晶体还是编程计算吧......
怎么样算匹配
前面我们说了,晶面间距和角度和标准图谱去对比。那么到底匹配到什么程度才能算匹配上了呢?
我个人的看法是倒空间矢量相差0.2~0.3(1/nm)可以接受,角度差距3°以内可以接受。如果样品存在大应变等过程,那么可以更放宽。当然,这纯属个人看法......


