一. 为什么需要可解释

几点考虑:

若模型完全黑箱, 会有信任风险, 虽然 Performance 不错, 但在医学诊断等严肃领域, 同样要关心诊断依据.
人类天生的好奇心, 也想知道不同特征到底作了怎样的贡献.
对模型预测的 badcase 作诊断, 增强洞察, 辅助模型与特征的迭代.

模型可解释其实就是想弄懂不同特征到底做了怎样的贡献, 从解释粒度上可以这么分类:

over the whole set
这种好理解, 求一个特征全局视角下的贡献, 可以直接从训练集中把它拎出来, 观察模型收敛后的指标变化.
for a particular prediction
深度模型效果更好的原因之一就是拥有强大的非线性拟合能力, 也就是说同一个特征下的同一个特征值, 会随样本的变化而体现出不同的贡献(受同一个样本内其他邻居特征的影响), 这就导致了仅有全局解释是不够的, 粒度需要细化到具体的单次预测上.
当能做到了单次预测, 自然也就能统计一个样本集合上的可解释数据了, 此时也拥有了全局视角. 所以本文工作搞单样本的可解释.

形式化定义

形式化的单样本可解释任务就是:

本文主角是 shap 库, 预备知识是联盟博弈论的 shapley-value.

二. 联盟博弈论中的 shapley-value

合作博弈论用于多人合作下的收益分配. 主要思想是: 列举出各种不同玩家之间的合作情况, 依据玩家参与与否的边际效应计算贡献.

直接用 shap 库中的公式了. 它是 classic Shapley value equation.
$\phi_i=\sum_{S \subseteq F \backslash\{i\}} \frac{|S| !(|F|-|S|-1) !}{|F| !}\left[f_{S \cup\{i\}}\left(x_{S \cup\{i\}}\right)-f_S\left(x_S\right)\right] \tag 2$

三. LIME 与 Kernel-Shap

在讲 Kernel-Shap 之前, 先引入预备知识 LIME.

Lime, Local Interpretable Model-Agnostic Explanations, 是 2017 年提出的一种模型无关的单样本预测解释方法(详见参考[9]). 核心思想是对于要解释的样本
, 把其特征划分为若干个组, 然后对此作局部采样, 得到新的人造样本集合 S. 然后 训练新的线性代理模型去学习原模型在样本S附近上的输出 .

公式化的表达就是:
$\xi(x)=\underset{g \in G}{\operatorname{argmin}} \ L \left(f, g, \pi_x\right)+\Omega(g) \tag 3$

上图是 lime 论文中的一个素材. 图片的原始特征是像素, 它就通过
选取图像区域作 super-pixel 的集合映射. 通过可解释分析, 验证了模型学到了预期之外的狼与雪地之间的相关性, 而没有学到因果层面的相关性.

Kernel-Shap

Kernal Shap method 是 LIME + Shapley values 的结合体. 乍一看式(2)与式(3)相去甚远, 但论文中讲到

LIME 是一种特征可加性方法(additive feature attribution method);
可加性方法中, 存在满足 {Local accuracy, Missingness, Consistency} 三大特性的唯一解;
而 shap-values 又是符合 LIME 方程约束下的同时具有上句提到的三大特性的唯一解.

就这么一通牵扯, 将二者结合到了一起.
LIME 呢, 可以解读为一种范式而不是确切的一个算法, 因为 loss function $的选取都是缺乏指导的, 而 Kernel Shap 将其作了具化, 满足了上文提到的三大特性. 图. 截取自原论文.$

additive 与三大特性

SHAP 是一类 additive feature attribution (满足可加性的特征归因) 方法. 该类方法更好地满足三大可解释性质:

local accuracy
consistency
当模型有变化, 一个特征变得更重要时, 其 feature attribution value 也不能变小.

四. Shap 库介绍及KernelSHAP实现

SH apley A dditive ex P lanation, 是一个py 三方库, 依据 合作博弈论 领域中的 shapley value 思想, 对模型的 单个预测 作解释.
它把特征比作博弈问题中的玩家, 模型预测比喻玩家合作之后的收益, 于是就顺畅了.

论文[4] 中, 它是这么说的:
“已有的多种方法 LIME, DeepLift 等, 它们之间的联系是啥? 什么情况下, 用其中一种会比另一种更好用?” 难以回答, 而它引入了 shapley 思想作了统一, 既有计算效率上的优化, 又更符合人类直觉.

基于 KernelSHAP 的实现的解释器叫 KernalExplainer.

传入待解释样本, 计算待解释的特征个数M
构造不同组合的合成(人造)样本
维护 maskMatrix, 样子见下:
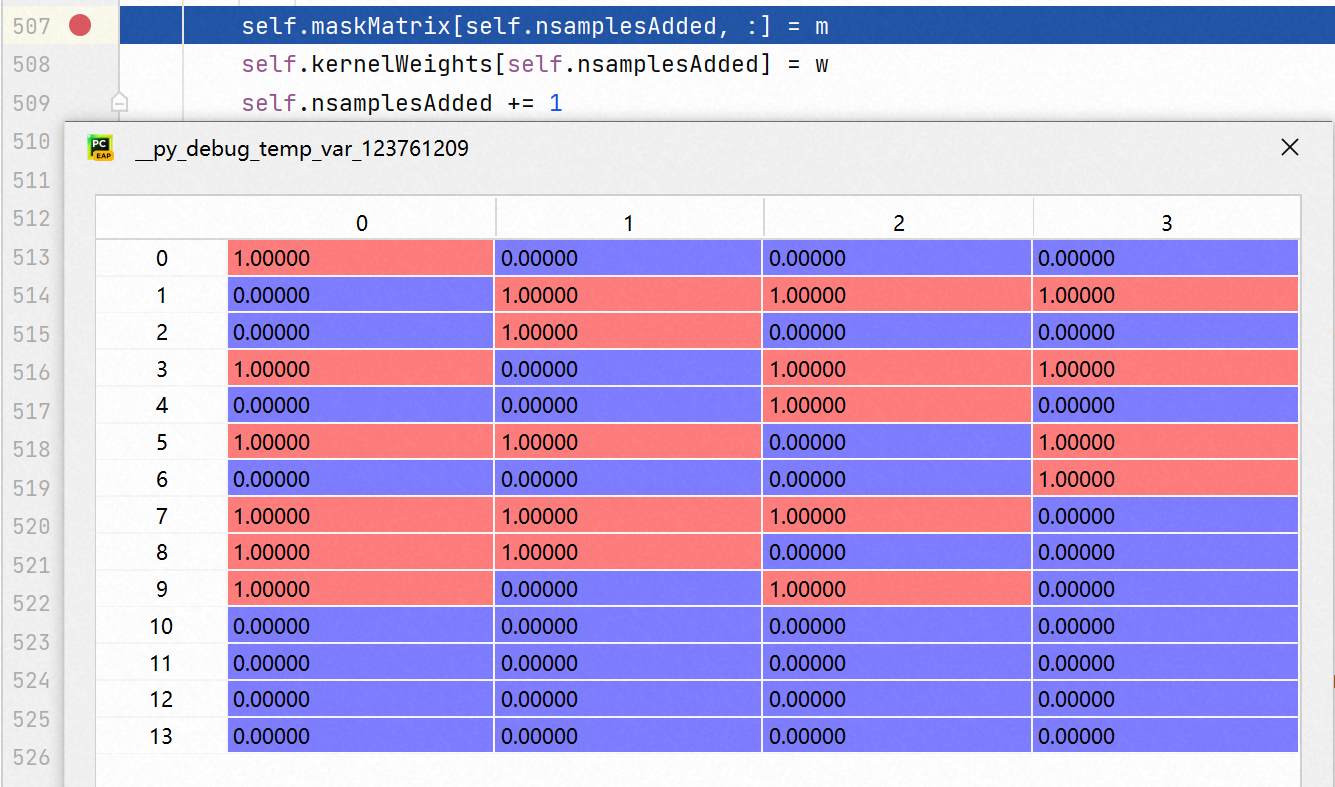
计算合成样本的输出
通过调用 run() 实现.
求解重要性
这里其实我不太懂. 原公式只是列出了单个特征的重要性求解方法. 但在 solve() 方法实现中, 是批量一次性求解的. 这里面的等价推导shap库没有给出讲解.

作了精简, 解读就在注释中.

class Kernel(Explainer):
    def __init__(self, model, data, link=IdentityLink(), **kwargs):
        model: callable对象, 传入特征即可输出结果.
        data: 用来估计数据集上的 期望, 随便传也不会影响一次可解释中的特征重要性
    def shap_values(self, X, **kwargs):
        """ 主方法 
        X 是待解释的样本, 单个样本解释时, shape 就是 (M,)
        # shape 恢复成了 [1,M]
        data = X.reshape((1, X.shape[0]))
        return self.explain(data, **kwargs)
    def explain(self, incoming_instance:np.ndarray, **kwargs):
        incoming_instance, 是待解释的样本特征
        # 自定义对象, instance.x = incoming_instance
        instance = convert_to_instance(incoming_instance)
        # 哪些特征是可变的, 用下标记录下来, 通常就是 从0到 incoming_instance.shape[1]
        self.varyingInds = self.varying_groups(instance.x)
        self.varyingFeatureGroups = [self.data.groups[i]
                                     for i in self.varyingInds]
        # 即 incoming_instance.shape[1]
        self.M = len(self.varyingFeatureGroups)
        # 原样本(非人造) 的预测结果, 就是待解释的结果
        self.fx = self.model.f(instance.x)
        # 为了控制计算复杂度, 这里限定总的人造样本数
        self.nsamples:int = kwargs.get('nsamples')
        self.allocate()
        # M-1 是因为要把待评估的单个特征摘出来, 除以2 是考虑到成对关系
        num_subset_sizes = np.int(np.ceil((self.M - 1) / 2.0))
        num_paired_subset_sizes = np.int(np.floor((self.M - 1) / 2.0))
        # 与论文 page-6 的 \pi x 权重相对应, 此时还没有 除以 C_M^{subset\_size}
        # weight_vector.shape = (num_subset_sizes,)
        # weight_vector[i] 表示 子集大小为 i+1 时的那些样本的权重之和
        weight_vector = np.array([(self.M - 1.0) / (i * (self.M - i)) for i in range(1, num_subset_sizes + 1)])
        weight_vector[:num_paired_subset_sizes] *= 2
        weight_vector /= np.sum(weight_vector)
        mask = np.zeros(self.M)
        remaining_weight_vector = copy.copy(weight_vector)
        num_samples_left = self.nsamples
        for subset_size in range(1, num_subset_sizes + 1):
            subsets_cnt_of_current_subset_size = binom(self.M, subset_size)
            if num_samples_left * remaining_weight_vector[subset_size - 1] / subsets_cnt_of_current_subset_size >= 1.0 - 1e-8:
                num_full_subsets += 1
                num_samples_left -= subsets_cnt_of_current_subset_size
                for inds_to_be_masked in itertools.combinations(group_inds, subset_size):
                    mask[:] = 0.0
                    mask[np.array(inds_to_be_masked, dtype='int64')] = 1.0
                    self.addsample(instance.x, mask, w)
                    # C_n^k 中的一种情况, 必然与 C_n^{n-k} 的一种情况是 取反的配对关系
                    # 所以可以一次加 俩 样本
                    if subset_size <= num_paired_subset_sizes:
                        mask[:] = np.abs(mask - 1)
                        self.addsample(instance.x, mask, w)
                    else:
                        logger.info(f"对于当前的 subsize={subset_size}, 在给定的总 nsamples={self.nsamples}"
                                    f" 约束下已经不能完全枚举作预测了. 作 跳出 动作")
                        break                        
        # 在给定的总样本量约束下, 若 未能全部展开计算, 需要随机采样
        if num_full_subsets != num_subset_sizes:
            # choice() 方法用法, 从 [0, a) 中完成 size 个抽样, 会有重复(有放回抽样)
            # size 为 [1,num_full_subsets) 的 subset 的样本已经添加完毕, 现在只添加后面的
            subset_size_choice = np.random.choice(a=list(range(num_full_subsets+1,
                                                            len(weight_vector)+1)),
                                        # 4倍是为了给去重留 buffer
                                        size=4 * samples_left,
                                        p=remaining_weight_vector)
            ind_set_pos = 0
            while samples_left > 0 and ind_set_pos < len(ind_set):
                mask.fill(0.0)
                # we call np.random.choice once to save time and then just read it here
                subset_size = subset_size_choice[ind_set_pos]
                ind_set_pos += 1
                # 这三行讲 怎么确定 subset_size 下的 subset, 具体哪几个特征其 mask=1
                random_enable_index = np.random.permutation(self.M)
                index_arr = random_enable_index[:subset_size]
                mask[index_arr] = 1.0
                # 虽然这里 w 是 1.0,但不起作用, 因为后面 还要去改 self.kernelWeights[nfixed_samples:]
                self.addsample(instance.x, mask, w=1.0)
            # 就是这里会 覆盖掉上面的 w=1.0
            self.kernelWeights[nfixed_samples:] *= weight_left / self.kernelWeights[nfixed_samples:].sum()
        self.run()
        phi = self.solve()
        return phi
    def allocate(self):
        """ 初始化 mask矩阵, 权重矩阵, 人造样本的预测结果数组 和 人造样本特征.
        self.maskMatrix = np.zeros((self.nsamples, self.M))
        self.kernelWeights = np.zeros(self.nsamples)
        self.y = np.zeros((self.nsamples, self.D))
        self.synth_data = np.tile(self.data.data, (self.nsamples, 1))
    def addsample(self, x, m, w):
        mask = m == 1.0
        evaluation_data = x[0, groups]
        self.synth_data[offset:offset + self.N, groups] = evaluation_data
        self.maskMatrix[self.nsamplesAdded, :] = m
        self.kernelWeights[self.nsamplesAdded] = w
        self.nsamplesAdded += 1
    def run(self):
        data = self.synth_data[self.nsamplesRun * self.N:self.nsamplesAdded * self.N, :]
        modelOut = self.model.f(data)
        self.y[self.nsamplesRun * self.N:self.nsamplesAdded * self.N, :] = np.reshape(modelOut, (num_to_run, self.D))
    def solve(self, fraction_evaluated, dim):
        w_aug = np.hstack((self.kernelWeights * (self.M - s), self.kernelWeights * s))
        w_sqrt_aug = np.sqrt(w_aug)
        eyAdj_aug = np.hstack((eyAdj, eyAdj - (self.link.f(self.fx[dim]) - self.link.f(self.fnull[dim]))))
        eyAdj_aug *= w_sqrt_aug
        mask_aug = np.transpose(w_sqrt_aug * np.transpose(np.vstack((self.maskMatrix, self.maskMatrix - 1))))
        coef_ = LassoLarsIC(criterion=c).fit(mask_aug, eyAdj_aug).coef_
        nonzero_inds = np.nonzero(coef_)[0]
        # eliminate one variable with the constraint that all features sum to the output
        eyAdj2 = eyAdj - self.maskMatrix[:, nonzero_inds[-1]] * (
        self.link.f(self.fx[dim]) - self.link.f(self.fnull[dim]))
        # solve a weighted least squares equation to estimate phi
        tmp = np.transpose(np.transpose(etmp) * np.transpose(self.kernelWeights))
        w = np.dot(tmp2, np.dot(np.transpose(tmp), eyAdj2))
        phi = np.zeros(self.M)
        phi[nonzero_inds[:-1]] = w
        phi[nonzero_inds[-1]] = (self.link.f(self.fx[dim]) - self.link.f(self.fnull[dim])) - sum(w)
五. shap 库其他 Explainer
 
LinearExplainer
 
用于 逻辑回归 模型的可解释, 背后算法是 DeepLIFT algorithm (Deep SHAP) , 官网的例子见 参考[2].
 Note that with a linear model the SHAP value for feature i for the prediction  $是数据集中特征i的取值的期望. 可以看出来针对LR, shap 几乎啥都没做.$  
DeepExplainer
 
用于 Deep NN 的模型可解释, 原理是 shap 与 ,官网例子见 参考[3].
 注意用到了 keras, tensoflow, shap 三个库, 很容易有版本不兼容问题, 导致示例代码不能顺利运行.
 类shap.explainers._deep.Deep继承了shap.explainers._explainer.Explainer, 根据model框架不同, 具体干活的又分为 TFDeep 与 PyTorchDeep. 
PartitionExplainer
 
见我的另一篇文章, 参考[10]. 
github, shap
代码例子, Sentiment Analysis with Logistic Regression
代码例子, deepexplainer
shap 三方包的论文, a-unified-approach-to-interpreting-model-predictions.pdf
划分树, 联盟划分, owen 计算等, Mutual information-based group explainers with coalition structure
 for machine learning model explanations
知乎文章, 关于Shapley Value（夏普利值）的公式
shap库 文档, Brute Force Kernel SHAP
Erik Štrumbelj and Igor Kononenko. “Explaining prediction models and individual predictions with feature contributions”. In: Knowledge andd information systems 41.3 (2014), pp. 647–665.
Lime paper, “Why Should I Trust You?”: Explaining the Predictions of Any Classifier
my blog, shap 中 PartitionExplainer 原理解读与官方demo的调试笔记
                    模型的评测指标只能反映它准不准, 如果没有好的可解释性, 人们就会担心它不够鲁棒, 难以放心去投用.SHAP 是一个库, 依据 组合博弈论领域 中的 shapely value 思想, 对模型的单个预测作解释.shapely valuetransformer 搭配...
				博鲁塔沙普
BorutaShap是一种包装器特征选择方法，它结合了Boruta特征选择算法和Shapley值。 事实证明，这种组合在速度和生成的特征子集的质量上都无法执行原始的排列重要性方法。 该算法不仅提供了更好的特征子集，而且还可以同时提供最准确和一致的全局特征等级，也可用于模型推断。 与原始R包（将用户限制为随机森林模型）不同，BorutaShap允许用户在特征选择过程中选择任何基于树的学习器作为基础模型。
 尽管BorutaShap的运行时性能有所提高，但是SHAP TreeExplainer随观察次数线性增长，这使得它在处理大型数据集时非常麻烦。 为了解决这个问题，BorutaShap包含了一个采样过程，该过程使用算法每次迭代时可用数据的最小可能子采样。 它通过比较样本的隔离林产生的分布和使用ks-test的数据来找到该样本。 从实验来看，此过程可以将运行时间减少多达80％，同时
论文：A Unified Approach to Interpreting ModelPredictions
论文地址：https://papers.nips.cc/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf
在SHAP论文中的Experiments部分，提出了一个可解释模型的评估指标：比较不同算法找出的最重要的特征的实际影响
如下图所示，对20张图片
在建立模型之前，特征重要性能够帮助训练模型，防止过拟合，提升模型的RUC效果。
建立模型之后，特征重要性能够增强模型（集成模型 非深度学习模型）的可解释性，帮助建立模型信任、做出现实意义上的决策。
建模前特征重要性判别
要构建数值型连续变量的监督学习模型，最重要的方面之一就是好好理解特征。观察一个模型的部分依赖图有助于理解模型的...
				文章目录简介定义性质举例1：手套博弈举例2
沙普利值是合作博弈理论中的一个概念，由劳埃德-沙普利在1951年提出了这个概念，并因此在2012年获得了诺贝尔经济学奖。对于每个合作博弈，它为所有玩家的联盟产生的总盈余分配了一个独特的分配。沙普利值的特点是有一系列的理想属性。
其设置如下：一个玩家联盟进行合作，并从合作中获得一定的整体收益。由于一些玩家对联盟的贡献可能大于其他玩家，或者可能拥有不同的讨价还价能力（例如威胁要破坏整个盈余），在任何特定的游戏中，所产生的盈余在玩家之间的最终分配应该是什么？或者换
				Shapley Value（沙普利值）是一种用于解决合作博弈（cooperative game）中资源分配问题的方法。在神经网络领域，可以将神经网络看作一个合作博弈中的参与者，每个参与者都会对最终的预测结果做出贡献。Shapley Value 的目的是评估每个参与者对最终预测结果的贡献，以便更公平地分配资源。
Shapley Value 的核心思想是基于每个参与者的边际贡献，即他们在参与者集合中的加入对最终结果的影响。具体来说，Shapley Value 将参与者的收益函数定义为一个排列（permutation）上的函数，表示参与者加入排列时对最终结果的影响。通过对不同排列的收益函数求平均值，可以得到每个参与者的 Shapley Value，表示该参与者对最终结果的贡献。
在神经网络中，可以将每个神经元视为一个参与者，根据其在神经网络中的贡献计算其 Shapley Value。这样就可以得到每个神经元对最终预测结果的贡献，以便更公平地分配资源，比如选择哪些神经元进行剪枝（pruning）等操作。