Diffusion Models:生成扩散模型
Diffusion Models:生成扩散模型
当前的内容是梳理 《Transformer视觉系列遨游》 系列过程中引申出来的。目前最近在AI作画这个领域 Transformer 火的一塌糊涂,AI画画效果从18年的 DeepDream[1] 噩梦中惊醒过来,开始从2022年 OpenAI 的 DALL·E 2[2] 引来插画效果和联想效果都达到惊人效果。虽然不懂,但是这个话题很吸引ZOMI,于是就着这个领域内容来看看有什么好玩的技术点。

但是要了解: Transformer 带来AI+艺术,从语言开始遇到多模态,碰撞艺术火花 这个主题,需要引申很多额外的知识点,可能跟 CV、NLP 等领域大力出奇迹的方式不同,AI+艺术会除了遇到 Transformer 结构以外,还会涉及到 VAE、ELBO、Diffusion Model等一系列跟数学相关的知识。
Transformer + Art系列中,今天新挖一个 Diffusion Models 的坑,跟 VAE 一样原理很复杂,实现很粗暴。据说生成扩散模型以数学复杂闻名,似乎比 VAE、GAN 要难理解得多,是否真的如此?扩散模型能少来点数学吗?扩散模型真的做不到一个简单点的理解吗?
在本文中,我们将研究扩散模型的理论基础,然后演示如何在 PyTorch 中使用扩散模型生成图像。Let's dive in!
Diffusion Model 基本介绍
扩散模型(Diffusion Models)发表以来其实并没有收到太多的关注,因为他不像 GAN 那样简单粗暴好理解。不过最近这几年正在生成模型领域异军突起,当前最先进的两个文本生成图像——OpenAI 的 DALL·E 2和 Google 的 Imagen,都是基于扩散模型来完成的。

如今生成扩散模型的大火,则是始于2020年所提出的 DDPM(Denoising Diffusion Probabilistic Model),仅在 2020 年发布的开创性论文 DDPM 就向世界展示了扩散模型的能力,在图像合成方面击败了 GAN[6],所以后续很多图像生成领域开始转向 DDPM 领域的研究。
看了下网上很多文章在介绍 DDPM 时,上来就引入概率转移分布,接着就是变分推断,然后极大值似然求解和引入证据下界(Evidence Lower Bound)。一堆数学记号下来,先吓跑了前几周的我(当然,从这种介绍我们可以再次看出,DDPM 实际上与 VAE 的理论关系是非常紧密),再加之人们对传统扩散模型的固有印象,所以就形成了“需要很高深的数学知识”的错觉。
生成模型对比
还是先横向对一下最近比较火的几个生成模型 GAN、VAE、Flow-based Models、Diffusion Models。
GAN 由一个生成器(generator)和判别器(discriminator)组成,generator 负责生成逼真数据以“骗”过 discriminator,而 discriminator 负责判断一个样本是真实的还是“造”出来的。GAN 的训练其实就是两个模型在相互学习,能不能不叫“对抗”,和谐一点。
VAE 同样希望训练一个生成模型 x=g(z),这个模型能够将采样后的概率分布映射到训练集的概率分布。生成隐变量 z,并且 z 是及含有数据信息又含有噪声,除了还原输入的样本数据以外,还可以用于生成新的数据。
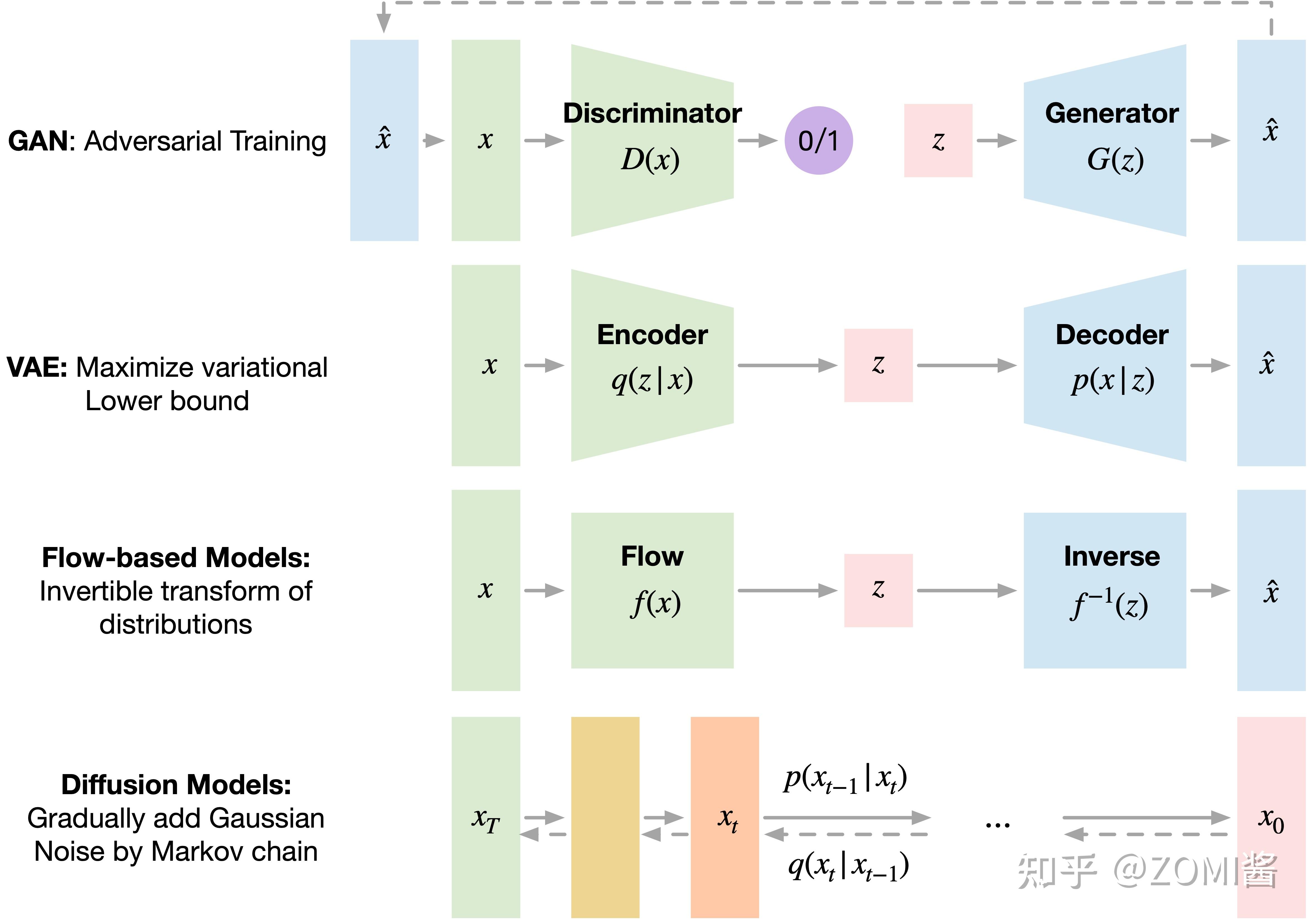
Diffusion Models 的灵感来自 non-equilibrium thermodynamics (非平衡热力学)。理论首先定义扩散步骤的马尔可夫链,以缓慢地将随机噪声添加到数据中,然后学习逆向扩散过程以从噪声中构造所需的数据样本。与 VAE 或流模型不同,扩散模型是通过固定过程学习,并且隐空间 z 具有比较高的维度。
总的来看,Diffusion Models 领域正处于一个百花齐放的状态,这个领域有一点像 GAN 刚提出来的时候,目前的训练技术让 Diffusion Models 直接跨越了 GAN 领域调模型的阶段,直接可以用来做下游任务。
基本介绍
Diffusion Models 既然叫生成模型,这意味着 Diffusion Models 用于生成与训练数据相似的数据。从根本上说,Diffusion Models 的工作原理,是通过连续添加高斯噪声来破坏训练数据,然后通过反转这个噪声过程,来学习恢复数据。
训练后,可以使用 Diffusion Models 将随机采样的噪声传入模型中,通过学习去噪过程来生成数据。也就是下面图中所对应的基本原理,不过这里面的图仍然有点粗。

更具体地说,扩散模型是一种隐变量模型(latent variable model),使用马尔可夫链(Markov Chain, MC)映射到 latent space。通过马尔科夫链,在每一个时间步 t 中逐渐将噪声添加到数据 x_i 中以获得后验概率 q(x_{1:T} \mid x_{0}) ,其中 {x_1, \ldots, x_T} 代表输入的数据同时也是 latent space。也就是说 Diffusion Models 的 latent space 与输入数据具有相同维度。
马尔可夫链(Markov Chain, MC)是概率论和数理统计中具有马尔可夫性质(Markov property)且存在于离散的指数集(index set)和状态空间(state space)内的随机过程(stochastic process)。
Diffusion Models 分为正向的扩散过程和反向的逆扩散过程。下图为扩散过程,从 x_0 到最后的 x_T 就是一个马尔科夫链,表示状态空间中经过从一个状态到另一个状态的转换的随机过程。而下标则是 Diffusion Models 对应的图像扩散过程。
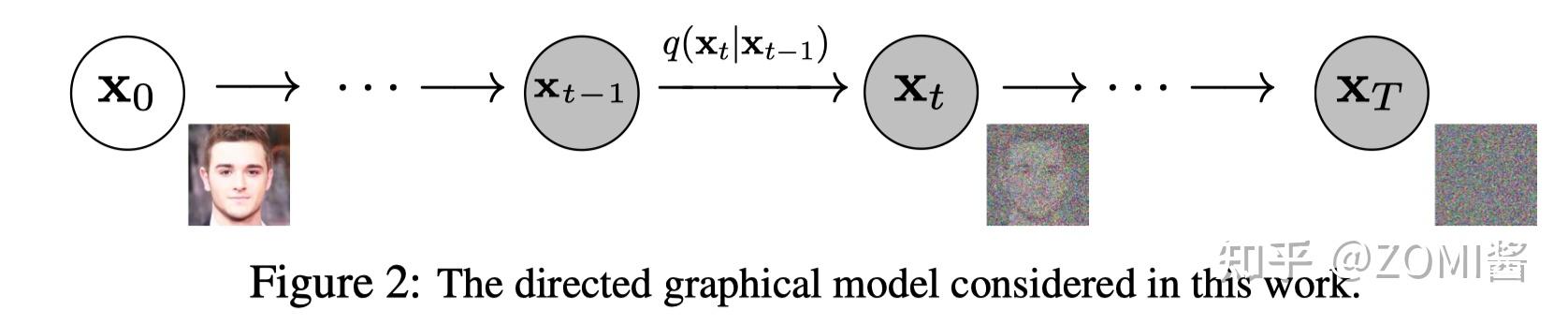
最终,从 x_0 输入的真实图像,经过 Diffusion Models 后被渐近变换为纯高斯噪声的图片 x_T 。
模型训练主要集中在逆扩散过程。训练扩散模型的目标是,学习正向的反过程:即训练概率分布 p_{\theta}(x_{t-1} \mid x_{t}) 。通过沿着马尔科夫链向后遍历,可以重新生成新的数据 x_0 。读到这里就有点意思啦,Diffusion Models 跟 GAN 或者 VAE 的最大区别在于不是通过一个模型来进行生成的,而是基于马尔科夫链,通过学习噪声来生成数据。

除了生成很好玩的高质量图片之外呢,Diffusion Models 还具有许多其他好处,其中最重要的是训练过程中不需要再对抗了,整个世界都感觉和平了。因为对于 GAN 网络模型来说,对抗性训练其实是很不好调试的,因为对抗训练过程互相博弈的两个模型,对我们来说是个黑盒子。另外在训练效率方面,扩散模型还具有可扩展性和可并行性,那这里面如何加速训练过程,如何添加更多数学规则和约束,扩展到语音、文本、三维领域就很好玩了,可以出很多新文章。
详解 Diffusion Model
上面已经清晰表示了 Diffusion Models 由正向过程(或扩散过程)和反向过程(或逆扩散过程)组成,其中输入数据逐渐被噪声化,然后噪声被转换回源目标分布的样本。
如果不想深入了解数学原理的可以直接跳过到代码实现部分。如果还是想了解一些基础的数学原理,那么可以接着继续看,其实没比 GAN 难多少,就是个马尔科夫链 + 条件概率分布。 核心在于如何使用神经网络模型,来求解马尔科夫过程的概率分布 。
扩散和逆扩散过程
前向过程由于每个时刻 t 只与 t-1 时刻有关,所以可以看做马尔科夫过程,在马尔科夫链的前向采样过程中,也就是扩散过程中可以将数据转换为高斯分布。即扩散过程通过 T 次累积对输入数据 x_i 添加高斯噪声,将这个跟马尔可夫假设相结合,于是可以对扩散过程表达成:
q(x_{1:T} \mid x_{0}) := \prod_{t=1}^{T} q(x_{t} \mid x_{t-1}) \\ := \prod_{t=1}^{T} \mathcal{N}(x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathbf{I}) \tag{1}
其中 \beta_{1}, \ldots, \beta_{T} 是高斯分布方差的超参数。在扩散过程中,随着 t 的增大, x_t 越来越接近纯噪声。当 T 足够大的时候, x_T 可以收敛为标准高斯噪声 \mathcal{N}(0, I) 。

不过呢,扩散模型的神奇“魔力”来自逆扩散过程。如果说扩散过程是加噪的过程,那么逆扩散过程就是去噪推断过程。如果我们能够逐步得到逆转后的分布 p_{\theta}(x_{t-1} \mid x_{t}) ,就可以从标准高斯分布 \mathcal{N}(0, I) 还原出样本数据的分布 x_0 。
也就是在训练时候,模型学习逆扩散过程的概率分布,以生成新数据。如下图所示,从纯高斯噪声 p(x_T):=\mathcal{N}(x_T; 0, \mathbf{I}) 开始,模型将学习联合概率分布 p_{\theta}(x_{T:0}) :
p_{\theta}(x_{T:0}):=p(x_{T}) \prod_{t=1}^{T} p_{\theta}(x_{t-1} \mid x_{t}) \\ :=p(x_{T}) \prod_{t=1}^{T} \mathcal{N}(x_{t-1} ; \boldsymbol{\mu}_{\theta}(x_{t}, t), \mathbf{\Sigma}_{\theta}(x_{t}, t)) \tag{2}
根据马尔可夫规则表示,逆扩散过程当前时间步 t 只取决于上一个时间步 t-1,所以有:
p_{\theta}(x_{t-1} \mid x_{t}):=\mathcal{N}(x_{t-1} ; \boldsymbol{\mu}_{\theta}(x_{t}, t), \mathbf{\Sigma}_{\theta}(x_{t}, t)) \tag{3}

现在我们其实已经简单搞清楚了 Diffusion Models 的扩散过程和逆扩散过程,也就是扩散过程中,人工添加一点点噪声直到数据为纯高斯噪声;逆扩散过程学习逆转后的分布,逐步地恢复样本数据。
不过,马尔科夫过程最麻烦的就是求解了,一般会用蒙特卡洛法进行采样,然后再去评估采样的结果好坏。上面的 Diffusion Models 会不会太理想啦?
训练方式
搞清楚逆扩散过程之后,现在算是搞清楚去噪推断过程。但是如何训练 Diffusion Models 以求得公式 (3) 中的均值 \boldsymbol{\mu}{\theta}(x{t}, t) 和方差 \mathbf{\Sigma}{\theta}(x{t}, t) 呢?
在 VAE 中我们学过极大似然估计的作用: 对于真实的训练样本数据已知,要求模型的参数,可以使用极大似然估计 。Diffusion Models 通过极大似然估计,来找到逆扩散过程中马尔科夫链转换的概率分布,这就是 Diffusion Models 的训练目的。即最大化模型预测分布的对数似然:
\mathcal{L}=\mathbb{E}_{q}[-\log p_{\theta}(x_{0})] \tag{4}
对于神经网络模型来说,一般优化的方式是通过损失函数求解网络模型的最小值,求最大化期望不太好使。于是换个思路,求模型的极大似然估计,等同于求解最小化负对数似然的变分上限 L_{vlb} (Variational Upper Bound):
\mathbb{E}[-\log p_{\theta}(x_{0})] \leq \mathbb{E}_{q}[-\log \frac{p_{\theta}(x_{0: T})}{q(x_{1: T} \mid x_{0})}]=: L_{vlb} \tag{5}
因为变分上界比较难求,但是 VAE 的推导中介绍过其实可以通过 KL散度来表示上界。那到这里为止, 最小化 L_{vlb} 即可最小化 Diffusion Models 的目标损失 。
看到公式 (5) 会不会觉很熟悉,下面讲讲两个小概念,再引入如何求解最小化变分上限 L_{vlb} 。
什么是KL散度呢?
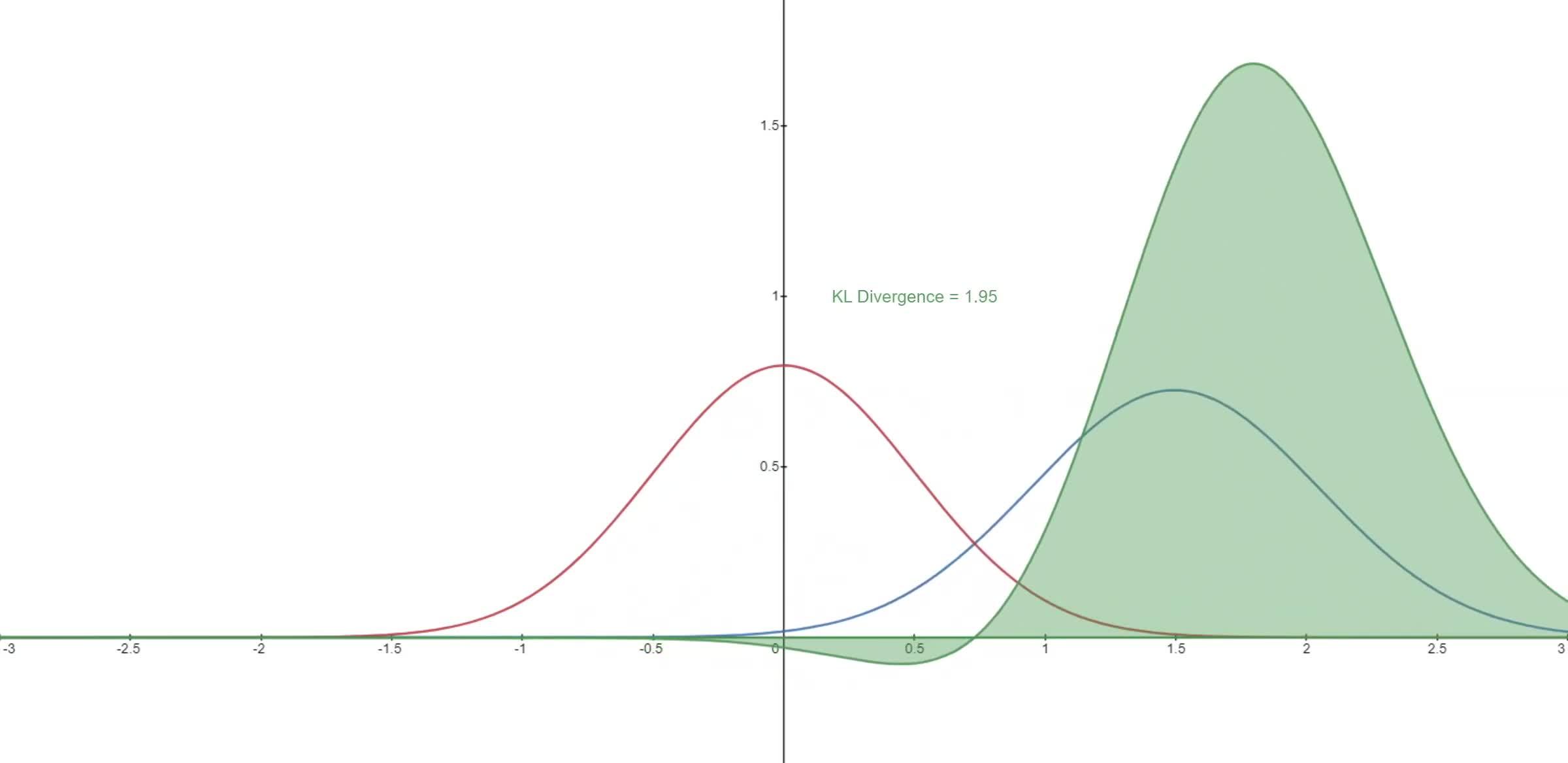
我们回顾一下, KL 散度是一种不对称统计距离度量,用于衡量一个概率分布 P 与另外一个概率分布 Q 的差异程度。之所以想根据 KL 散度来求解 L_{vlb} ,是因为根据 Diffusion Models 的定义马尔可夫链中的转移分布属于高斯分布,而 KL 散度则可以用来计算2个高斯分布之间的差异距离。
连续分布的 KL 散度的数学形式是:
D_{\mathrm{KL}}(P \| Q)=\int_{-\infty}^{\infty} p(x) \log (\frac{p(x)}{q(x)}) d x \tag{6}
 https://www.zhihu.com/video/1538310598659530752
https://www.zhihu.com/video/1538310598659530752
用 KL 散度来表示变分上界
根据 Diffusion Models 最早提出的一篇文章[1],进一步对 L_{vlb} 推导,可以得到变分上限为熵与多个KL散度的累加,根据 KL 散度重写变分上限有:
L_{vlb}=L_{0}+L_{1}+\ldots+L_{T-1}+L_{T} \tag{7}
其中有:
L_{0}=-\log p_{\theta}(x_{0} \mid x_{1}) \tag{8}
L_{t-1}=D_{KL}(q(x_{t-1} \mid x_{t}, x_{0}) \| p_{\theta}(x_{t-1} \mid x_{t})) \tag{9}
L_{T}=D_{KL}(q(x_{T} \mid x_{0}) \| p(x_{T})) \tag{10}
x_0 都会出现在扩散过程中的 L_{t-1} ,现在所有 KL 散度都是在高斯概率分布之间进行比较。 这意味着可以使用闭包表达式,而不是采样的蒙特卡洛估计方式来精确计算变分上界。
到这里看不懂没关系,想表达的是最小化 L_{vlb} 即可最小化 Diffusion Models 的目标损失,而求解 L_{vlb} 则可以通过计算 KL 散度来代替。
有了目标函数的数学基础后,现在需要就如何实现扩散模型训练过程有几个细节:
-
对于正向扩散过程,唯一需要的选择是概率相关的向量(均值和方差),其值在扩散过程中在隐变量
x_t
中直接添加高斯参数
\beta_{t}
。
-
对于逆扩散过程,需要选择能够表达高斯分布的模型结构,神经网络模型的拟合能力很强,于是就可以引入神经网络模型啦。
-
最后就是对于神经网络模型有一个简单的要求,模型的输入、输出、中间隐变量必须要有相同的维度 dims。
损失函数和 L_T
既然有神经网络模型,那自然离不开损失函数,有了损失函数就有了优化的方向和目标,下面来展开损失函数的定义。
在扩散过程公式(1)中,其中 \beta 1, \ldots, \beta T 是高斯分布方差的超参数。且实际中 \beta_t 随着 t 增大是递增的,即 \beta_1 < \ldots < \beta_T 。在实际代码中,我们设置 \beta_t 是从 0.0001 到0.02 线性插值。
在逆扩散过程公式(10)中,时间步 T 中前,由于前向扩散过程中 q 没有可学习参数,只是单纯添加高斯噪声,而最后时间步 T 得到的 x_T 则是纯高斯噪声,因此在训练的过程中 L_T 可以当做常量忽略。即下面公式不需要:
L_{T}=D_{KL}(q(x_{T} \mid x_{0}) \| p(x_{T})):= 0
回顾公式(3),把反向马尔科夫过程转变为高斯分布来表示:
p_{\theta}(x_{t-1} \mid x_{t}):=\mathcal{N}(x_{t-1} ; \boldsymbol{\mu}_{\theta}(x_{t}, t), \mathbf{\Sigma}_{\theta}(x_{t}, t)) \tag{3}
在求解(训练)的过程需要知道得到高斯分布的均值 \boldsymbol{\mu}{\theta}(x{t}, t) 和方差 \mathbf{\Sigma}{\theta}(x{t}, t) 。对于方差 \Sigma 不好求解,DDPM 论文中直接使用 \beta_{t} 来代替:
\boldsymbol{\Sigma}_{\theta}(x_{t}, t)=\sigma_{t}^{2} \mathbb{I} \sigma_{t}^{2}=\beta_{t} \tag{11}
假设多元高斯是具有相同方差的独立高斯的乘积,方差值可以随时间变化 。基于这个假设可以将逆扩散过程的方差,设置为与正向扩散过程方差相同,得到公式(11)。不过有意思的是在实际代码中因为引入了神经网络,所以可以通过训练的方式来得到方差 \Sigma 。
数学上,假设使用 \beta_{t} 来代替方差 {\Sigma}_{\theta} ,因此有:
p_{\theta}(x_{t-1} \mid x_{t}):=\mathcal{N}(x_{t-1} ; \boldsymbol{\mu}_{\theta}(x_{t}, t), \boldsymbol{\Sigma}_{\theta}(x_{t}, t) \\ :=\mathcal{N}(x_{t-1} ; \boldsymbol{\mu}_{\theta}(x_{t}, t), \sigma_{t}^{2} \mathbf{I}) \tag{12}
那现在就更清楚啦,可以将KL散度:
L_{t-1}=D_{KL}(q(x_{t-1} \mid x_{t}, x_{0}) \| p_{\theta}(x_{t-1} \mid x_{t})) \tag{13}
转换为:
L_{t-1} \propto\|\tilde{\mu}_{t}(x_{t}, x_{0})-\mu_{\theta}(x_{t}, t)\|^{2} \tag{14}
由正向扩散过程我们知道,任意时刻的 x_t 可以由 x_0 和 \beta 表示。参数 \mu_{\theta} 最直接的表示是预测扩散模型的后验概率的均值。不过在实际测试当中,DDPM 作者发现通过训练以在任何给定时间步 t 预测噪声分量 \mu_{\theta} 会产生更好的结果。设:
\boldsymbol{\mu}_{\theta}(x_{t}, t)=\frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon}_{\theta}(x_{t}, t)) \tag{15}
其中:
\alpha_{t}:=1-\beta_{t} \text { and } \bar{\alpha}_{t}:=\prod_{s=1}^{t} \alpha_{s} \tag{16}
因此可以得到损失函数 L,使得训练更加稳定:
L_{\text {simple }}(\theta):=\mathbb{E}_{t, x_{0}, \epsilon}[\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_{\theta}(\sqrt{\bar{\alpha}_{t}} x_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}, t)\|^{2}] \tag{17}
高斯分布 {\epsilon} 为神经网络模型所预测的噪声(用于去噪),可看做为 {\epsilon}{\theta}(x_t, t) 。 Diffusion Models 训练的核心就是取学习高斯噪声 {\epsilon}, {\epsilon}{\theta} 之间均方误差 MSE 。
实际训练过程和 L_0
上面已经说过啦,在逆扩散过程中,马尔科夫过程表示为由连续条件高斯分布下的累积变换组成。有了总体的优化策略,还要看每个像素的计算方式,在逆扩散过程结束时,我们希望得到一张生成好的图像,因此需要设计一种方法,使得图像上每个像素值都满足离散的对数似然。
为了达到这个目的,将逆扩散过程中的最后从 x_1 到 x_0 的转换设置为独立的离散计算方式。 即在最后一个转换过程在给定 x_1$ x_1 下得到图像 x_0 满足对数似然,假设像素与像素之间是相互独立的:
p_{\theta}(x_{0} \mid x_{1})=\prod_{i=1}^{D} p_{\theta}(x_{0}^{i} \mid x_{1}^{i}) \tag{18}

式 (18) 中 D 是输入数据的维数,上标 i 表示图像中的一个坐标位置。现在的目标是确定给定像素的值可能性有多大,也就是想要知道对应时间步 t=1 下噪声图像 x 中相应像素值的分布:
\mathcal{N}(x ; \mu_{\theta}^{i}(x_{1}, 1), \sigma_{1}^{2}) \tag{19}
其中 t = 1 的像素分布来自多元高斯分布,其对角协方差矩阵允许我们将分布拆分为单变量高斯的乘积:
\mathcal{N}(x ; \mu_{\theta}(x_{1}, 1), \sigma_{1}^{2} \mathbb{I})=\prod_{i=1}^{D} \mathcal{N}(x ; \mu_{\theta}^{i}(x_{1}, 1), \sigma_{1}^{2}) \tag{20}
现在假设图像已经从0-255的数值之间,经过归一化在[-1,1]的范围内。在 t=0 时给定每个像素的像素值,最后一个时间步 t=1 的转换概率分布 p_{\theta}(x_{0} \mid x_{1}) 的值就是每个像素值的乘积。简而言之,这个过程由等式简洁 (18) 地表示:
p_{\theta}(x_{0} \mid x_{1})=\prod_{i=1}^{D} p_{\theta}(x_{0}^{i} \mid x_{1}^{i}) \\ =\prod_{i=1}^{D} \int_{\delta_{-}(x_{0}^{i})}^{\delta_{+}(x_{i}^{i})} \mathcal{N}(x ; \mu_{\theta}^{i}(x_{1}, 1), \sigma_{1}^{2}) dx \tag{21}
其中约束有:
\delta_{-}(x)= \begin{cases}-\infty & x=-1 \\ x-\frac{1}{255} & x>-1\end{cases}
和:
\delta_{+}(x)= \begin{cases}\infty & x=1 \\ x+\frac{1}{255} & x<1\end{cases}
那现在我们就可以计算公式 (8) 中,最后的转换概率分布 p_{\theta}(x_{0} \mid x_{1}) 的值。
训练过程如图左边 Algorithm 1 Training部分:
-
从标准高斯分布采样一个噪声
\epsilon \sim \mathcal{N}(0, \mathbf{I})
;
-
通过梯度下降最小化损失
\nabla_{\theta}|\boldsymbol{\epsilon}-\mathbf{z}{\theta}(\sqrt{\bar{\alpha}{t}} x_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}, t)|^{2}
;
-
训练到收敛为止(训练时间比较长,T代码中设置为1000)
测试(采样)如图右边 Algorithm 2 Sampling部分:
-
从标准高斯分布采样一个噪声
x_T \sim \mathcal{N}(0, \mathbf{I})
;
-
从时间步 T 开始正向扩散迭代到时间步 1;
-
如果时间步不为1,则从标准高斯分布采样一个噪声
z \sim \mathcal{N}(0, \mathbf{I})
,否则 z=0;
-
根据高斯分布计算每个时间步 t 的噪声图;

网络模型
虽然通过上面一连串很复杂或者看不懂的公式,其实就是为了得到损失函数,或者要知道 Diffusion Model 的优化目标。简化损失函数后的目标变得更加简单了,主要是训练模型 {\epsilon}_{\theta} 。但是看了很多文章,其实还停留在复杂的数学公式推导,仍然没有定义 Diffusion Model 的网络模型结构。
在定义网络模型之前呢,再次声明,Diffusion Model 中对模型的唯一要求是输入和输出的数据维度 dims 需要相同。有点意思,看到这句话,估计就会想到类似于 U-Net的模型架构,而不是 VAE 那种 Encoder 和 Decoder 对 Latency sapce 压缩的结构啦。

Pytroch 实现
扩散过程
在扩散过程公式(1)中,其中 \beta 1, \ldots, \beta T 是高斯分布方差的超参数。且实际中 \beta_t 随着 t 增大是递增的,即 \beta_1 < \ldots < \beta_T 。在下面实际代码中,我们使用numpy设置 \beta_t 是从 0.0001 到0.02 线性插值linspace,然后再转换称为Pytroch的tensor。对应时间步T,即num_steps设置为1000。
回顾扩散过程的公式(1):
q(x_{1:T} \mid x_{0}) := \prod_{t=1}^{T} q(x_{t} \mid x_{t-1}) := \prod_{t=1}^{T} \mathcal{N}(x_{t} ; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t} \mathbf{I}) \tag{1}
为了方便表达,假设 \alpha_{t}=1-\beta_{t} ,和 \bar{\alpha}{t}=\prod_{s=1}^{t} \alpha_{s} ,那么有:
q(x_{t} \mid x_{0})=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{t-1},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right) \tag{22}
所以代码中 alphas 即对应 \alpha_{t} ,alphas_prod对应 \bar{\alpha}_{t} 。然后先计算得到公式 (22) 中的变量。
num_steps = 1000
beta = torch.tensor(np.linspace(1e-5, 0.2e-2, num_steps))
alphas = 1 - betas
alphas_prod = torch.cumprod(alphas, 0)
alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0)
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)既然有了公式(22) 中的变量, q(x_{1:T} \mid x_{0}) 的函数表示就变得比较简单啦,直接使用下面函数 q_x 来表示。
def q_x(x_0, t, noise=None):
if not noise: noise = torch.randn_like(x_0)
alphas_t = extract(alphas_bar_sqrt, t, x_0)
alphas_1_m_t = extract(one_minus_alphas_bar_sqrt, t, x_0)
return (alphas_t * x_0 + alphas_1_m_t * noise)正向过程正式的计算比较简单直接,正如上面理论部分提到的,通过时间步 T 在每次马尔科夫链的转换过程对样本数据 dataset 添加噪声:
for i in range(num_steps):
q_i = q_x(dataset, torch.tensor([i]))对应公式求解 q(x_{t} \mid x_{0}) 则为:
posterior_mean_coef_1 = (betas * torch.sqrt(alphas_prod_p) / (1 - alphas_prod))
posterior_mean_coef_2 = ((1 - alphas_prod_p) * torch.sqrt(alphas) / (1 - alphas_prod))
posterior_variance = betas * (1 - alphas_prod_p) / (1 - alphas_prod)
posterior_log_variance_clipped = torch.log(torch.cat((posterior_variance[1].view(1, 1), posterior_variance[1:].view(-1, 1)), 0)).view(-1)
def q_posterior_mean_variance(x_0, x_t, t):
coef_1 = extract(posterior_mean_coef_1, t, x_0)
coef_2 = extract(posterior_mean_coef_2, t, x_0)
mean = coef_1 * x_0 + coef_2 * x_t
var = extract(posterior_log_variance_clipped, t, x_0)
return mean, var训练过程
与正向扩散过程不同,逆扩散过程需要训练神经网络模型,这里通过定义损失函数和训练参数,然后进行训练。
损失函数刚才原理部分已经讲过啦,通过最小化数据的负对数似然的变分上限进行求解,也就是对应公式(17)。而网络模型直接使用Unet,这里面就不再展开Unet的编写啦,网上一大堆。
from model import Unet
from ema import EMA
import torch.optim as optim
model = Unet()
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# Create EMA model
ema = EMA(0.9)
ema.register(model)
# Batch size
batch_size = 128
for t in range(num_steps):
# X is a torch Variable
permutation = torch.randperm(dataset.size()[0])
for i in range(0, dataset.size()[0], batch_size):
# Retrieve current batch
indices = permutation[i:i+batch_size]
batch_x = dataset[indices]
# Compute the loss.
loss = noise_estimation_loss(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)
# Before the backward pass, zero all of the network gradients
optimizer.zero_grad()
# Backward pass: compute gradient of the loss with respect to parameters
loss.backward()
# Perform gradient clipping
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.)
# Calling the step function to update the parameters
optimizer.step()
# Update the exponential moving average
ema.update(model)
# Print loss
if (t % 100 == 0):
print(loss)参考公式(17)的实现损失函数,在上面训练的过程中其实没有展开,下面给出简单的代码示例,有空再详细解读,今天有点肚子痛,赶着收工。
def noise_estimation_loss(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
batch_size = x_0.shape[0]
# Select a random step for each example
t = torch.randint(0, n_steps, size=(batch_size // 2 + 1,))
t = torch.cat([t, n_steps - t - 1], dim=0)[:batch_size].long()
# x0 multiplier
a = extract(alphas_bar_sqrt, t, x_0)
# eps multiplier
