用3D点云重建三维模型网格【Python】

本文将介绍 使用 python 从点云快速创建网格的3D 表面重建过程，你可以导出、可视化并将结果集成到最喜欢的 3D 软件中，而无需任何编码经验。此外，我们还将介绍一种生成多个细节级别 (LoD) 的简单方法，如果你想创建实时应用程序（例如使用 Unity 的虚拟现实），这将非常有用。

3D 网格是几何数据结构，通常由一堆连接的三角形组成，这些三角形明确地描述了一个表面 。它们用于从地理空间重建到视觉特效、电影和视频游戏的广泛应用。我们经常在需要物理副本时创建它们，或者如果我需要在游戏引擎中整合环境，而点云支持有限的时候，这就变得很重要。

3D网格很好地集成在大多数与软件专业人员一起工作的软件中。最重要的是，如果想探索 3D 打印的奇迹，你需要能够从拥有的数据中生成一致的网格。本文旨在通过 5 个可自定义的步骤为你提供高效的工作流程，以及本文末尾的远程可执行脚本。让我们开始！

1、设置环境

在上一篇文章中，我们看到了如何使用 Anaconda 轻松设置环境，以及如何使用 GUI Spyder 来管理你的代码。我们将继续以这种方式，仅使用 2 个库。

为了从点云中自动获取 3D 网格，我们将在我们的环境中添加另一个库 Open3D。它是一个开源库，允许使用一组高效的数据结构和算法进行 3D 数据处理。安装需要单击环境旁边的 ▶️ 图标。

打开终端并运行以下命令：

conda install -c open3d-admin open3d==0.8.0.0

注意 ： Open3D 包兼容 python 版本 2.7、3.5 和 3.6。如果你有另一个版本，最好创建一个新环境，或者通过在终端中键入命令 conda install python=3.5 来更改终端中的 python 版本。

这将自动安装包及其依赖项，你只需 y 在终端提示时输入以允许此过程，现在已为该项目进行了设置。

2、加载和准备数据

启动你的 python 脚本工具（Spyder GUI、Jupyter 或 Google Colab），我们将在其中调用 2 个库：Numpy 和 Open3D。

import numpy as np
import open3d as o3d

然后，我们创建保存数据路径和点云数据的变量：

input_path="your_path_to_file/"
output_path="your_path_to_output_folder/"
dataname="sample.xyz"
point_cloud= np.loadtxt(input_path+dataname,skiprows=1)

注意 ： 至于上一篇文章，我们将使用采样点云，你可以从 这个存储库 免费下载。如果想在不安装任何东西的情况下预先将其可视化，你可以查看 webGL 版本 。

最后，我们将 point_cloud 变量类型从 Numpy 转换为 Open3D o3d.geometry.PointCloud 类型以便进一步处理：

pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(point_cloud[:,:3])
pcd.colors = o3d.utility.Vector3dVector(point_cloud[:,3:6]/255)
pcd.normals = o3d.utility.Vector3dVector(point_cloud[:,6:9])

注意 ： 以下命令首先实例化 Open3d 点云对象，然后从原始 NumPy 数组中添加点、颜色和法线。

为了快速查看加载的内容，可以执行以下命令（在 Google Colab 中不起作用）：

o3d.visualization.draw_geometries([pcd])

3、选择网格化策略

现在我们准备通过对 pcd 点云进行网格划分来开始表面重建过程。我将给出我最喜欢的有效获得结果的方法，但在我们深入研究之前，需要一些浓缩的细节来掌握底层过程。我将限制自己使用两种啮合策略。

策略 1：球旋转算法 [1]

Ball-Pivoting Algorithm (BPA) 背后的想法是模拟使用虚拟球从点云生成网格。我们首先假设给定的点云由从物体表面采样的点组成。点必须 严格 表示一个表面（无噪声），重建的网格是明确的。

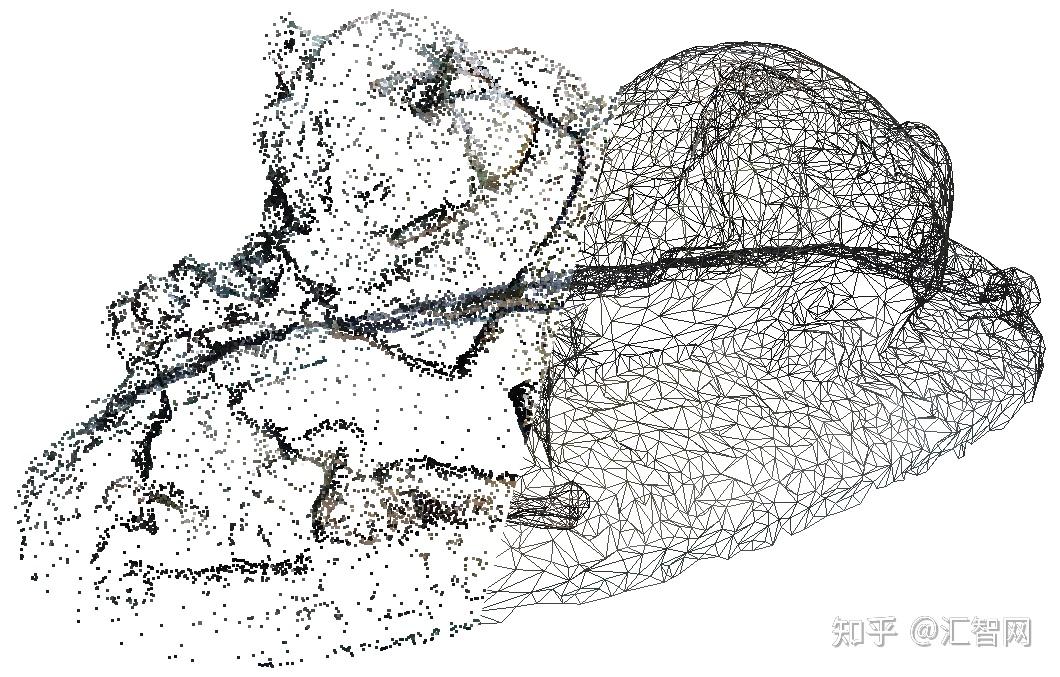
使用这个假设，想象在点云“表面”上滚动一个小球。这个小球取决于网格的比例，并且应该比点之间的平均间距略大。当你将球放到点的表面上时，球会被抓住并落在三个点上，这三个点将形成 种子三角形。从 那个位置，球沿着由两点形成的三角形边缘滚动。然后球会在一个新的位置安顿下来：一个新的三角形由之前的两个顶点形成，一个新的三角形被添加到网格中。当我们继续滚动和旋转球时，会形成新的三角形并将其添加到网格中。球继续滚动滚动，直到网格完全形成。

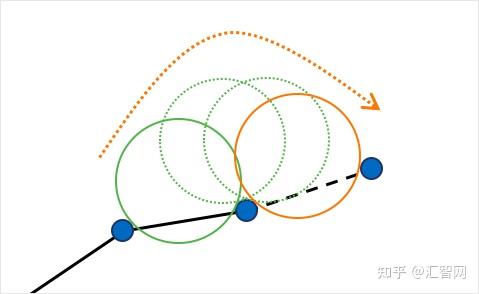
Ball-Pivoting Algorithm 背后的 想法 很简单，但当然，这里最初表达的过程有很多缺陷：

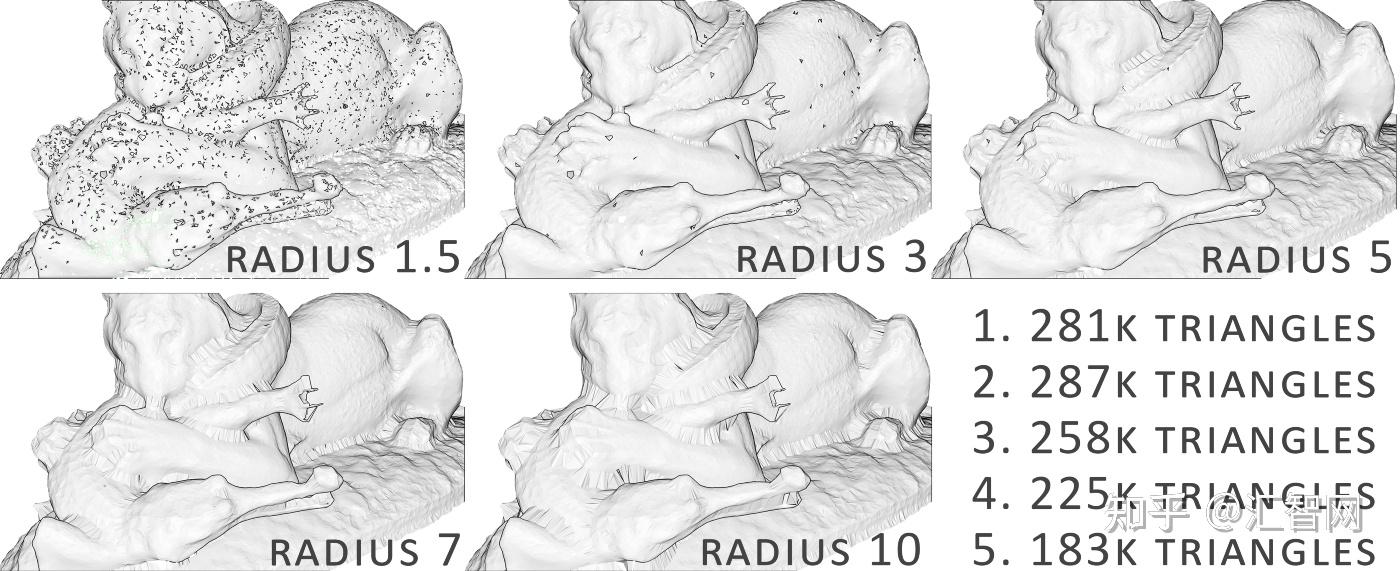
• 球半径如何选择？ 半径是根据输入点云的大小和比例凭经验获得的。理论上，球的直径应该略大于点之间的平均距离。
• 如果点在某些位置相距太远而球掉下来怎么办？ 当球沿边缘旋转时，它可能会错过表面上的适当点，而是撞到物体上的另一个点，甚至恰好是它的三个旧点。在这种情况下，我们检查新三角形的法线 Facet 是否与点的 Vertex 法线一致。如果不是，那么我们拒绝该三角形并创建一个洞。
• 如果表面有折痕或凹谷，使得表面与自身之间的距离小于球的大小怎么办？ 在这种情况下，球只会在折痕上滚动并忽略折痕内的点。但是，这不是理想的行为，因为重建的网格对对象不准确。
• 如果表面被分隔成点区域，使得球无法在这些区域之间成功滚动怎么办？ 虚拟球在不同位置多次落到表面上。这可确保球捕获整个网格，即使这些点的间距不一致。

策略2：泊松重建[2]

泊松重构更具技术性/数学性。它的方法被称为隐式网格划分方法，我将其描述为试图将数据“包裹”在光滑的布料中。在不涉及太多细节的情况下，我们尝试通过创建一个代表与法线链接的等值面的全新点集来拟合原始点集的防水表面。有几个可用的参数会影响网格划分的结果：

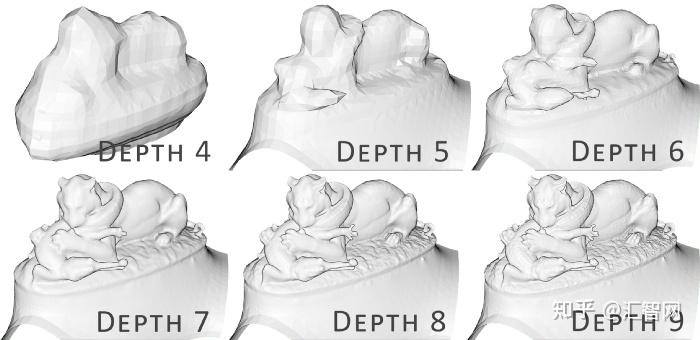
• 哪个深度？ 树深度用于重建。网格越高，网格越详细（默认值：8）。对于嘈杂的数据，您可以在生成的网格中保留异常值的顶点，但算法不会检测到它们。因此，较低的值（可能在 5 到 7 之间）会提供平滑效果，但会丢失细节。深度值越高，生成的网格的顶点数量就越高。

• 哪个宽度？ 这指定了树结构的最精细级别的目标宽度，称为八叉树 。别担心，我将在另一篇文章中介绍这个和最好的 3D 数据结构，因为它扩展了本文的范围。无论如何，如果指定了深度，则忽略此参数。
• 哪个尺度？ 它描述了用于重建的立方体的直径与样本边界立方体的直径之间的比率。非常抽象，默认参数通常效果很好（1.1）。

• 哪个适合？ linear_fit 参数如果设置为 true，则让重建器使用线性插值来估计等顶点的位置。

4、处理数据

策略 1：BPA

我们首先根据从所有点之间的距离计算出的平均距离来计算必要的半径参数：

distances = pcd.compute_nearest_neighbor_distance()
avg_dist = np.mean(distances)
radius = 3 * avg_dist

在一个命令行中，我们可以创建一个网格并将其存储在 bpa_mesh 变量中：

bpa_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(pcd,o3d.utility.DoubleVector([radius, radius * 2]))

在导出网格之前，我们可以将结果下采样到可接受数量的三角形，例如 100k 个三角形：

dec_mesh = mesh.simplify_quadric_decimation(100000)

此外，如果你认为网格会呈现一些奇怪的伪影，可以运行以下命令以确保其一致性：

dec_mesh.remove_degenerate_triangles()
dec_mesh.remove_duplicated_triangles()
dec_mesh.remove_duplicated_vertices()
dec_mesh.remove_non_manifold_edges()

策略二：泊松重构

注意 ： 该策略从Open3D 0.9.0.0 版本 开始可用，因此目前只能远程工作。 可以通过我在此处 提供的 google colab 代码执行它。

要使用泊松获得结果，非常简单。您只需要调整传递给函数的参数，如上所述：

poisson_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(pcd, depth=8, width=0, scale=1.1, linear_fit=False)[0]

注意 ： 该函数输出一个列表，该列表由一个 o3d.geometry 对象和一个 Numpy 数组组成。你只想选择最后证明 [0] 的 o3d.geometry。

为了获得干净的结果，通常需要添加一个裁剪步骤来清除下左图中以黄色突出显示的不需要的伪影：

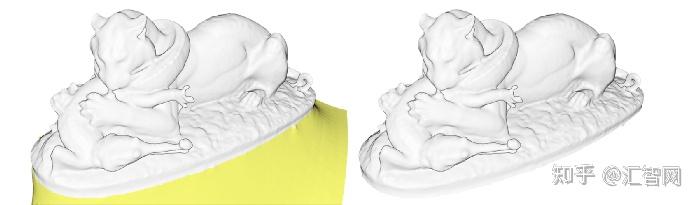
为此，我们计算包含原始点云的初始边界框，并使用它从边界框外的网格中过滤所有表面：

bbox = pcd.get_axis_aligned_bounding_box() 
p_mesh_crop = poisson_mesh.crop(bbox)

现在有一个或多个变量，每个变量都包含网格几何体，干得好！在应用程序中获取它的最后一步是导出它！

5、导出和可视化

使用该功能可以直接导出数据 write_triangle_mesh 。我们只需在创建的文件的名称中指定 .ply、.obj、.stl 或 .gltf 的扩展名，以及要导出的网格。下面，我们将 BPA 和 Poisson 的重建都导出为 .ply 文件：

o3d.io.write_triangle_mesh(output_path+"bpa_mesh.ply", dec_mesh)
o3d.io.write_triangle_mesh(output_path+"p_mesh_c.ply", p_mesh_crop)

为了快速生成细节级别 (LoD)，让我们编写你的第一个函数。这将非常简单。该函数将使用网格、LoD 列表（作为三角形的目标数量）、生成文件的文件格式和写入文件的路径作为参数。函数（在脚本中编写）如下所示：

def lod_mesh_export(mesh, lods, extension, path):
    mesh_lods={}