在LDA主题模型之后,需要对模型的好坏进行评估,以此依据,判断改进的参数或者算法的建模能力。
Blei先生在论文《Latent Dirichlet Allocation》实验中用的是Perplexity值作为评判标准。
一、Perplexity定义
源于wiki:
http://en.wikipedia.org/wiki/Perplexity
perplexity是一种信息理论的测量方法,b的perplexity值定义为基于b的熵的能量(b可以是一个概率分布,或者概率模型),通常用于概率模型的比较
wiki上列举了三种perplexity的计算:
1.1 概率分布的perplexity
其中H(p)就是该概率分布的熵。当概率P的K平均分布的时候,带入上式可以得到P的perplexity值=K。
1.2 概率模型的perplexity
公式中的Xi为测试局,可以是句子或者文本,N是测试集的大小(用来归一化),对于未知分布q,perplexity的值越小,说明模型越好。
指数部分也可以用交叉熵来计算,略过不表。
1.3单词的perplexity
perplexity经常用于语言模型的评估,物理意义是单词的编码大小。例如,如果在某个测试语句上,语言模型的perplexity值为2^190,说明该句子的编码需要190bits
二、如何对LDA建模的主题模型
Blei先生在论文里只列出了perplexity的计算公式,并没有做过多的解释。
在摸索过得知,M代表测试语料集的文本数量(即多少篇文本),Nd代表第d篇文本的大小(即单词的个数),P(Wd)代表文本的概率,文本的概率是怎么算出来的呢?
在解决这个问题的时候,看到rickjin这样解释的:
p(z)表示的是文本d在该主题z上的分布,应该是p(z|d)
这里有个误区需要注意:Blei是从每篇文本的角度来计算perplexity的,而rickjin是从单词的角度计算perplexity的,不要弄混了。
总结一下:
测试文本集中有M篇文本,对词袋模型里的任意一个单词w,P(w)=∑z p(z|d)*p(w|z),即该词在所有主题分布值和该词所在文本的主题分布乘积。
模型的perplexity就是exp^{ – (∑log(p(w))) / (N) },∑log(p(w))是对所有单词取log(直接相乘一般都转化成指数和对数的计算形式),N的测试集的单词数量(不排重)
评估LDA主题模型-perflexity
LDA主题模型好坏的评估,判断改进的参数或者算法的建模能力。
perplexity is only a crude measure, it's helpful (when using LDA) to get 'close' to the appropriate number of topics in a corpus.
Blei先生在论文《Latent Dirichlet Allocation》实验中用的是Perplexity值作为评判标准,并在论文里只列出了perplexity的计算公式。
Note
:M代表测试语料集的文本数量,Nd代表第d篇文本的大小(即单词的个数),P(Wd)代表文本的概率
文本的概率的计算:
p(z)表示的是文本d在该主题z上的分布,应该是p(z|d)
Note:
1.
Blei是从每篇文本的角度来计算perplexity的,而上面是从单词的角度计算perplexity。
2. 测试文本集中有M篇文本,对词袋模型里的任意一个单词w,P(w)=∑z p(z|d)*p(w|z),即该词在所有主题分布值和该词所在文本的主题分布乘积。
3. 模型的perplexity就是exp^{ - (∑log(p(w))) / (N) },∑log(p(w))是对所有单词取log(直接相乘一般都转化成指数和对数的计算形式),N的测试集的单词数量(不排重)
4. P(w)=∑z p(z|d)*p(w|z)这个w是测试集上的词汇
[
http://blog.csdn.net/pipisorry/article/details/42460023
]
[http://faculty.cs.byu.edu/~ringger/CS601R/papers/Heinrich-GibbsLDA.pdf - 29页]
Estimate the perplexity within gensim
The `LdaModel.bound()` method computes a lower bound on perplexity, based on a supplied corpus (~of held-out documents).
This is the method used in Hoffman&Blei&Bach in their "Online Learning for LDA" NIPS article.
[https://groups.google.com/forum/#!topic/gensim/LM619SB57zM]
假设我们有一些测试数据,test data.测试数据中有m个句子;s1,s2,s3…,sm
我们可以查看在某个模型下面的概率:
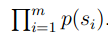
我们也知道,如果计算相乘是非常麻烦的,可以在此基础上,以另一种形式来计算模型的好坏程度。
在相乘的基础上,运用Log,来把乘法转换成加法来计算。
补充一下,在这里的p(Si)其实就等于我们前面所介绍的q(the|*,*)*q(dog|*,the)*q(…)…
有了上面的式子,评价一个模型是否好坏的原理在于:
a good model should assign as high probability as possible to these test data sentences.
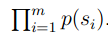 ,this value as being a measure of how well the alleviate to make sth less painful or difficult to deal with language model predict these test data sentences.
,this value as being a measure of how well the alleviate to make sth less painful or difficult to deal with language model predict these test data sentences.
The higher the better.
上面的意思也就是说,如果
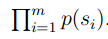 的值越大,那么这个模型就越好。
的值越大,那么这个模型就越好。
实际上,普遍的评价的指标是perplexity
其中,M的值是测试数据test data中的所有的数量。
那么从公式当中查看,可以知道。perplexity的值越小越好。
为了更好的理解perplexity,看下面这个例子:
我们现在有一个单词集V,N=|V|+1
有了上面的条件,可以很容易的计算出:
Perplexity是测试branching factor的数值。
branching factor又是什么呢?有的翻译为分叉率。如果branching factor高,计算起来代价会越大。也可以理解成,分叉率越高,可能性就越多,需要计算的量就越大。
上面的例子q=1/N只是一个举例,再看看下面这些真实的数据:
Goodman的结果,其中|V|=50000,在trigram model的
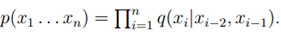 中,Perplexity=74
在bigram model中,
中,Perplexity=74
在bigram model中,
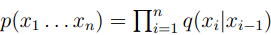 ,Perplexity=137
在unigram model中,
,Perplexity=137
在unigram model中,
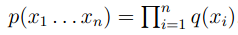 ,perplexity=955
,perplexity=955
在这里也看到了,几个模型的perplexity的值是不同的,这也就表明了三元模型一般是性能良好的。
[
评价一个语言模型Evaluating Language Models:Perplexity
]
皮皮blog
一种可能更好的主题模型评价标准
[Optimizing semantic coherence in topic models.]
from
:http://blog.csdn.net/pipisorry/article/details/42460023
ref:
Topic models evaluation in Gensim
http://stackoverflow.com/questions/19615951/topic-models-evaluation-in-gensim
http://www.52ml.net/14623.html
Ngram model and perplexity in NLTK
http://www.researchgate.net/publication/221484800_Improving_language_model_perplexity_and_recognition_accuracy_for_medical_dictations_via_within-domain_interpolation_with_literal_and_semi-literal_corpora
Investigating the relationship between language model perplexity and IR precision-recall measures.
LDA/NMF/LSA多模型/多主题一致性评价方法《
Exploring topic coherence over many models and many topics
》K Stevens, P Kegelmeyer, D Andrzejewski... [University of California Los Angeles] (2012)
GITHUB
论文:(概率)生成模型评价方法研究《
A note on the evaluation of generative models
》Lucas Theis, Aäron van den Oord, Matthias Bethge (2015)
Notes on A note on the evaluation of generative models
by Hugo Larochelle